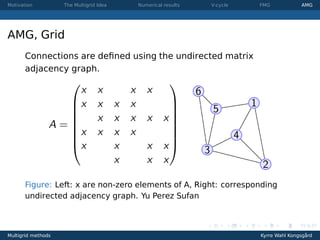
This document provides an overview of multigrid methods for solving elliptic PDEs such as Poisson's equation. It discusses the motivation for multigrid methods based on the error behavior of iterative methods like Jacobi. The core idea of multigrid is to introduce coarser grids where low-frequency errors become high-frequency, improving convergence. Details are provided on V-cycles and full multigrid methods for geometric problems, as well as algebraic multigrid which extends the approach to general matrices. Coarsening, interpolation, restriction, and the coarse-grid operator are defined algebraically.

1. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Multigrid methods
Geometric and Algebraic MGM
Kyrre Wahl Kongsgård
University of Amsterdam
http://student.science.uva.nl/∼kyrre/
Seminars Computational Science – April 18, 2011
Multigrid methods Kyrre Wahl Kongsgård

2. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Overview.
1 Motivation
A second look at the Jacobi method
Error behaviour
More on Errors
2 The Multigrid Idea
3 Numerical results
4 V-cycle
5 FMG
6 AMG
Multigrid methods Kyrre Wahl Kongsgård

3. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Poisson’s equation
As a motivating example we use the elliptic PDE:
uxx = f , 0 < x < 1
u(0) = u(1) = 0
Discretization on a uniform grid with mesh-size h gives the
familiar problem:
Au = f
Multigrid methods Kyrre Wahl Kongsgård

4. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Jacobi method
To solve Au = f we use the Jacobi method.
um+1 = D−1 (f − (L + U)um )
Eigenvalues λµ of the iteration matrix G = I − D−1 A.
µπ h
λµ = 1 − 2sin2 ( ) = cos(µπ h), µ = 1, 2, ..., n
2
with corresponding eigenvectors
√
vµ = 2h [sin(µπ h), sin(µπ 2h), ..., sin(µπ nh)]T (1)
Multigrid methods Kyrre Wahl Kongsgård

5. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Error analysis
Using the definition em = um − u∗ = Gm e0 we get the
expression:
n
em = cµ λm vµ
µ
µ=1
ρ(G) ≤ 1 is equivalent with convergence, but ...
Multigrid methods Kyrre Wahl Kongsgård

6. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Convergence
size matters!
Eigenvalues can be grouped into three sets:
µ
• N << 1: Eigenvalue is (positive) small, changes the error
correspondingly. Problem?
• µ ≈ N . Convergence is almost instantaneous.
2
• k ≈ N. Eigenvalue approaches -1, only changes sign of
error. Overshooting. This can taken care of by
damping.
Multigrid methods Kyrre Wahl Kongsgård

7. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Multigrid
The core idea of multigrid is to introduce a coarse grid where
smooth(low frequency) becomes oscillatory(high frequency)!
MGM v-cycle:
• Smoothing of the error (Jacobi/GS).
• Restriction to coarse grid.
• Smoothing on the coarse grid.
• Interpolation to fine grid.
Multigrid methods Kyrre Wahl Kongsgård

8. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Geometric multigrid in more detail
• Jacobi/GS: Ah u = bh .
• Restriction of the residual: r2h = Rh rh = R2h (bh − Ah u),
2h
h
• Jacobi/GS: A2h E2h = r2h
• Interpolation of E2h : Eh h
= I2h E2h . u∗ = u + Eh
• Jacobi/GS: Ah u∗ = bh .
Multigrid methods Kyrre Wahl Kongsgård

9. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Numerical results
MG applied to the model problem with f = 1.
2
Figure: Left: Error after 5 relaxed(ω = 3 ) Jacobi steps. Right: Error
after a single two-grid iteration. Hans Petter Langtangen, Aslak
Tveito.
Multigrid methods Kyrre Wahl Kongsgård

10. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
V-cycle
Figure: V-cycle, multiple-levels. Irad Yavneh
Multigrid methods Kyrre Wahl Kongsgård

11. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Full multigrid method
Figure: A schematic description of the full multigrid method. Irad
Yavneh
Multigrid methods Kyrre Wahl Kongsgård

12. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Algebraic Multigrid
Main ingredients of Geometric multigrid:
• Relaxation of high-freq errors.
• Several grids
• Interpolation and restriction operators
If we want to apply the MG idea to a general linear system,
several concepts must be defined:
• Grid.
• Algebraic smoothness.
• I, R, and A2 h
Multigrid methods Kyrre Wahl Kongsgård

13. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
AMG, Grid
Connections are defined using the undirected matrix
adjacency graph.
Figure: Left: x are non-zero elements of A, Right: corresponding
undirected adjacency graph. Yu Perez Sufan
Multigrid methods Kyrre Wahl Kongsgård

14. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Coarse grid
Strength of connection. Given a threshold
0 < θ ≤ 1, variable ui strongly depends on variable uj
if
−aij ≥ θ maxk=i {−aik }
The elements aij are divided into three sets:
• Ci (coarse, strong influence)
• Fi (fine, strong influence)
• Di (-, weak influence)
Multigrid methods Kyrre Wahl Kongsgård

15. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Coarse grid points
We need to determine the coarse values, which should have
properties:
• Algebraic smooth errors should be approximated well.
• Minimize the number of points.
• Coarse values surrounded by fine values.
Classic coarsening scheme:
• 1. Choose strongly connection node as a coarse node.
• 2. Strong connections are marked as fine.
• 3. Repeat on sub-graph.
Multigrid methods Kyrre Wahl Kongsgård

16. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Algebraic Smoothness
The error e is algebraic smooth if en+1 ≈ en , i.e.
e ≈ (I − ω D−1 A)e
or
Ae = 0 ⇒ −aii ei ≈ aij ej
j =i
Multigrid methods Kyrre Wahl Kongsgård

17. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Interpolation
From the definition of algebraic smoothness (e ∈ null(A))
aii ei ≈ − aij ej − aij ej − aij ej
j∈Ci j∈Fi j∈Di
Interpolation formula:
ei , i ∈ Ci
(Ih e)i =
2h
j∈Ci ωij ej , i ∈ Fi
aim amj
aij + m∈F ( )
k∈Ci amk
ωij = −
aii + n∈D ain
Multigrid methods Kyrre Wahl Kongsgård

18. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Restriction and A2h
The restriction operator is defined as the transpose of the
interpolation operator.
2h
Rh = IhT
2h
and for the coarse-grid operator A2h is defined using the
Galerkin product
2h h
A2h = Rh Ah I2h
Multigrid methods Kyrre Wahl Kongsgård

19. Motivation The Multigrid Idea Numerical results V-cycle FMG AMG
Acknowledgements
This lecture is copy-paste compilation of several similar
introductions to geometric and algebraic multi grid methods,
[1], [2], [3]
Gilbert Strang.
Computational Science and Engineering.
Wellesley-Cambridge Press, 1st edition, 2007.
Irad Yavneh.
Why multigrid methods are so efficient.
Computing in Science and Engineering, 8:12–22, 2006.
Robert D. Falgout.
An introduction to algebraic multigrid.
Computing in Science and Engineering, 8:24–33, 2006.
Multigrid methods Kyrre Wahl Kongsgård