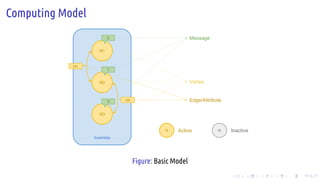
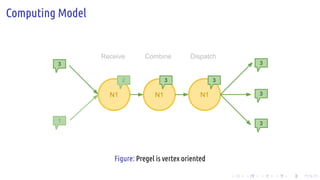
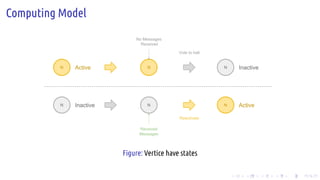
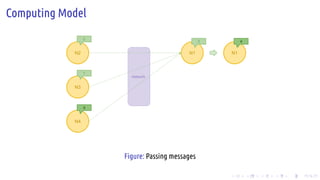
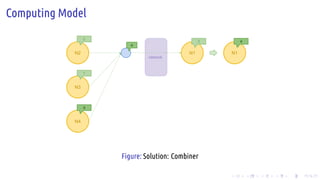
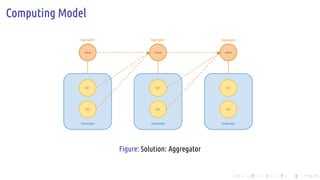
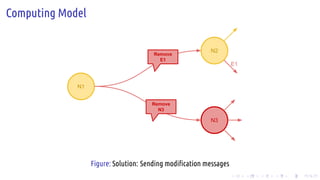
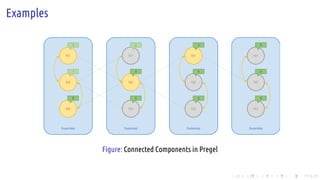
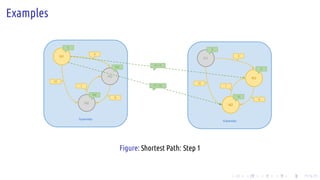
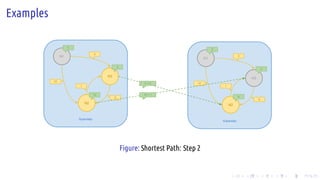
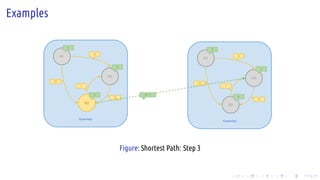
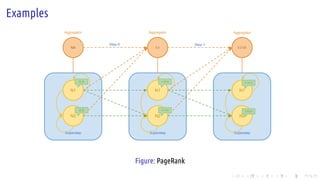
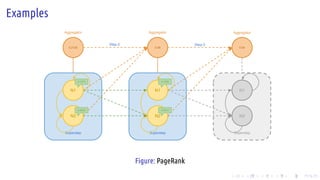
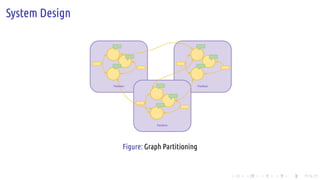
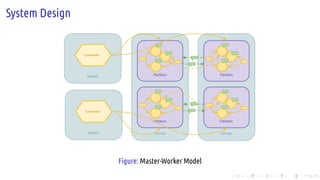
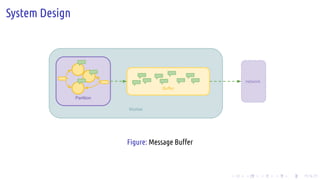
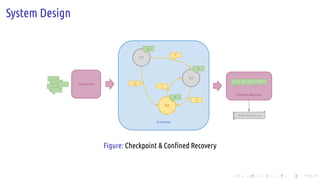
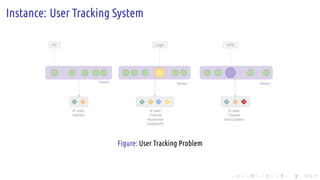
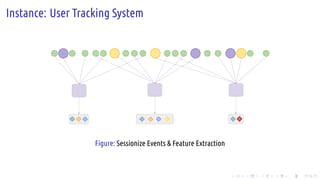
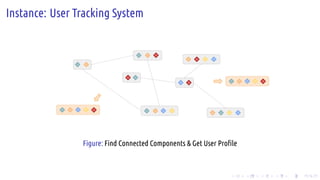
The document discusses the Pregel computing model, a distributed graph computing system developed by Google, designed for processing large-scale graph data. It describes the model's architecture, including concepts like supersteps, message passing, combiners, and aggregators, as well as practical examples such as finding connected components and shortest paths. Additionally, the document covers system design features like graph partitioning, master-worker architecture, and strategies for managing network traffic and checkpoints.

1. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Pregel In Graphs
Models & Instances
Chase Zhang
Strikingly
March 16, 2018

2. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Table of Contents
Computing Model
Examples
System Design
Instance: User Tracking System

3. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
What is Pregel?
▶ Published by Google at 20091
▶ Distributed graph computing system at large scale
▶ Implemented by open source solutions like Spark’s GraphX2
1
https://kowshik.github.io/JPregel/pregel_paper.pdf
2
https://spark.apache.org/graphx/

4. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
Superstep
N1
N2
N3
2
1
3
Message
Vertex
Edge/Attribute
attr
attr
N Active N Inactive
Figure: Basic Model

5. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
N1N1
1
3
2
N1
3
3
3
3
Receive Combine Dispatch
3
Figure: Pregel is vertex oriented

6. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
N Active
N Inactive
N N Inactive
N N Active
No Messages
Received
Vote to halt
Received
Messages
Reactivate
Figure: Vertice have states

7. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
▶ Pregel is a vertex oriented computing model.
▶ Map runs upon each vertex (other than edges)
▶ Each vertex only knows its out-going edges during each superstep
▶ Pregel depends on message sending to iteratively computing the result
▶ Each vertex receives messages from prior step
▶ After one step, vertices send messages to adjacent vertices
▶ Vertices have states
▶ Only active vertices will send message to the others
▶ Program terminates once there is no active vertices

8. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
Problem
Sending message through network is costly.

9. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
network
N2
N3
N4
2
1
4
N1
3
N1
4
Figure: Passing messages

10. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
network
N2
N3
N4
2
1
4
N1
3
N1
4
4
Figure: Solution: Combiner

11. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
Problem
Some iterative graph algrithms require graph-wide results and metrics.

12. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
Superstep
N1
Superstep
N1
Superstep
N1
value value value
Aggregator Aggregator Aggregator
N2 N2 N2
Figure: Solution: Aggregator

13. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
Problem
Some graph algorithms require modifying topology during iteration.

14. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
N1
N2
N3
Remove
E1
Remove
N3
E1
Figure: Solution: Sending modification messages

15. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Computing Model
▶ Pregel provides combiner for reducing network traffic
▶ Pregel provides aggregator for recording graph-wide values and metrics
▶ Vertices in Pregel can send topology modification requests as messages to target
vertices

16. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Problem
Find connected components of a directed graph.

17. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Solution
(Single machine) Union-Find3
.
3
https://en.wikipedia.org/wiki/Disjoint-set_data_structure

18. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Solution
(Pregel) Emit max(min) message received until no active vertex.

19. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
N2
N3
2
1
3
Superstep
N1
N2
N3
2
3
3
Superstep
N1
N2
N3
3
3
3
Superstep
N1
N2
N3
3
3
3
Figure: Connected Components in Pregel

20. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Problem
Find shortest path from a single source to the other vertices.

21. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Solution
(Single machine) Dijkstra4
, Bellman-Ford5
, A*6
.
4
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
5
https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
6
https://en.wikipedia.org/wiki/A*_search_algorithm

22. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Solution
(Pregel) BFS, emitting current shortest cost from source vertex to current vertex plus edge
cost.

23. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
N2
N3
0
INF
INF
10
3
6
Superstep
N1
N2
N3
0
3
10
10
3
6
0 + 3
0 + 101 1
Figure: Shortest Path: Step 1

24. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
N2
N3
0
3
10
10
3
6
Superstep
N1
N2
N3
0
3
9
10
3
6
3 + 6
10 + 1
1 1
Figure: Shortest Path: Step 2

25. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
N2
N3
0
3
9
10
3
6
Superstep
N1
N2
N3
0
3
9
10
3
6
9+ 1
1 1
Figure: Shortest Path: Step 3

26. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Problem
PageRank7
7
https://en.wikipedia.org/wiki/PageRank

27. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
|V| vertices number
|E(v)| edges number of vertex v
val(v) current message value of v
sum(v) sum of messages received of v in last superstep
▶ Initial messages: 1
|V|
▶ Emit messages: val(v)
|E(v)|
▶ Update value: sum(v) · 0.85 + 0.15
|V|

28. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
Superstep
N1
Superstep
N1
NA 0.5 0.2125
Aggregator Aggregator Aggregator
N2 N2 N2
0.5
0.5
0.2875
0.7125
0.1972
0.8028
Step-0 Step-1
Figure: PageRank

29. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Examples
Superstep
N1
Superstep
N1
Superstep
N1
0.2125 0.09 0.04
Aggregator Aggregator Aggregator
N2 N2 N2
0.1972
0.8028
0.1588
0.8412
Step-3Step-2
Figure: PageRank

30. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
▶ Graph partitioning
▶ Master-worker system model
▶ Message buffer for better performance
▶ Checkpoint and confined recovery

31. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
Partition Partition
Partition
Figure: Graph Partitioning

32. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
▶ Graph is partitioned by hash(vertexId) by default
▶ User partitioning function can be provided for locality

33. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
Worker
Partition
Partition
Worker
Partition
Partition
Master
Coordinator
Master
Coordinator
Figure: Master-Worker Model

34. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
▶ Master coodinates supersteps, it holds no partition of graph
▶ Master calculate and hold values of aggregators
▶ Master send RPC to every participated worker and wait for task to finish
▶ Workers hold partitions of graph. Given a vertexId, a worker can know which worker
is holding it without querying master

35. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
Worker
Partition
Buffer
network
Figure: Message Buffer

36. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
Confined Recovery
Superstep
N1
N2
N3
0
3
9
10
3
6
1
Checkpoint
Write Ahead Log
Figure: Checkpoint & Confined Recovery

37. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
System Design
▶ A worker buffers message locally and send them as a batch as to reduce network
overhead
▶ Before and after a superstep, a worker checkpoint and perform confined recovery
▶ Confined recovery logs every outgoing messages, so that only lost partitions need to
be recalculated

38. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
PV Login GPS
IP addr
ClientId
IP addr
ClientId
Nickname
AvatarURL
IP addr
ClientId
GeoLocation
Session
Session Session
Figure: User Tracking Problem

39. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Figure: Sessionize Events & Feature Extraction

40. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Figure: Find Connected Components & Get User Profile

41. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Problem
Calculating edges betwen sessions cost O(N2
) time if we compare each pair. It will be too
enormous even for just a million(106
) sessions.

42. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Solution
Five significant features are selected for matching, and we define two sessions are
matched if more than two features matched. So we can:
▶ Enumerate combinations of the five significant features, it will be C2
5 = 10
▶ Applying sort or hash method to distribute sessions into matching buckets
▶ Connect sessions in a same bucket

43. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Figure: Match Features

44. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Instance: User Tracking System
Claim
This optimization (using sort method) reduced time cost.
At first, the total elements to match upon each other will increasee to O(N × 10). To sort
all elements cost O(log N × 10). Connect elements in a bucket cost O(N × 10) in total.
The final cost will be
O(log N × 10) ≃ O(log N) ⪯ O(N2
)

45. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Thank you!