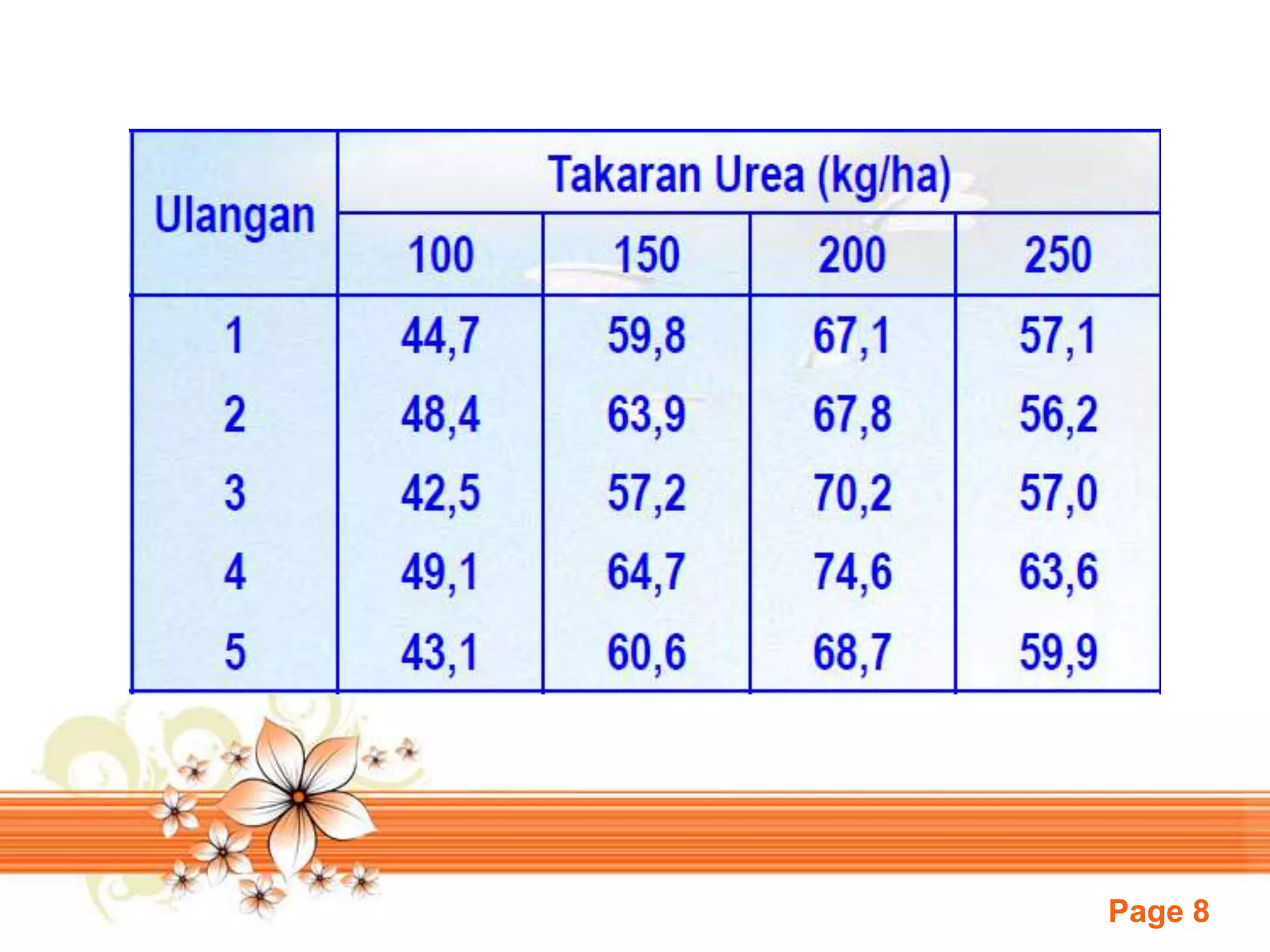
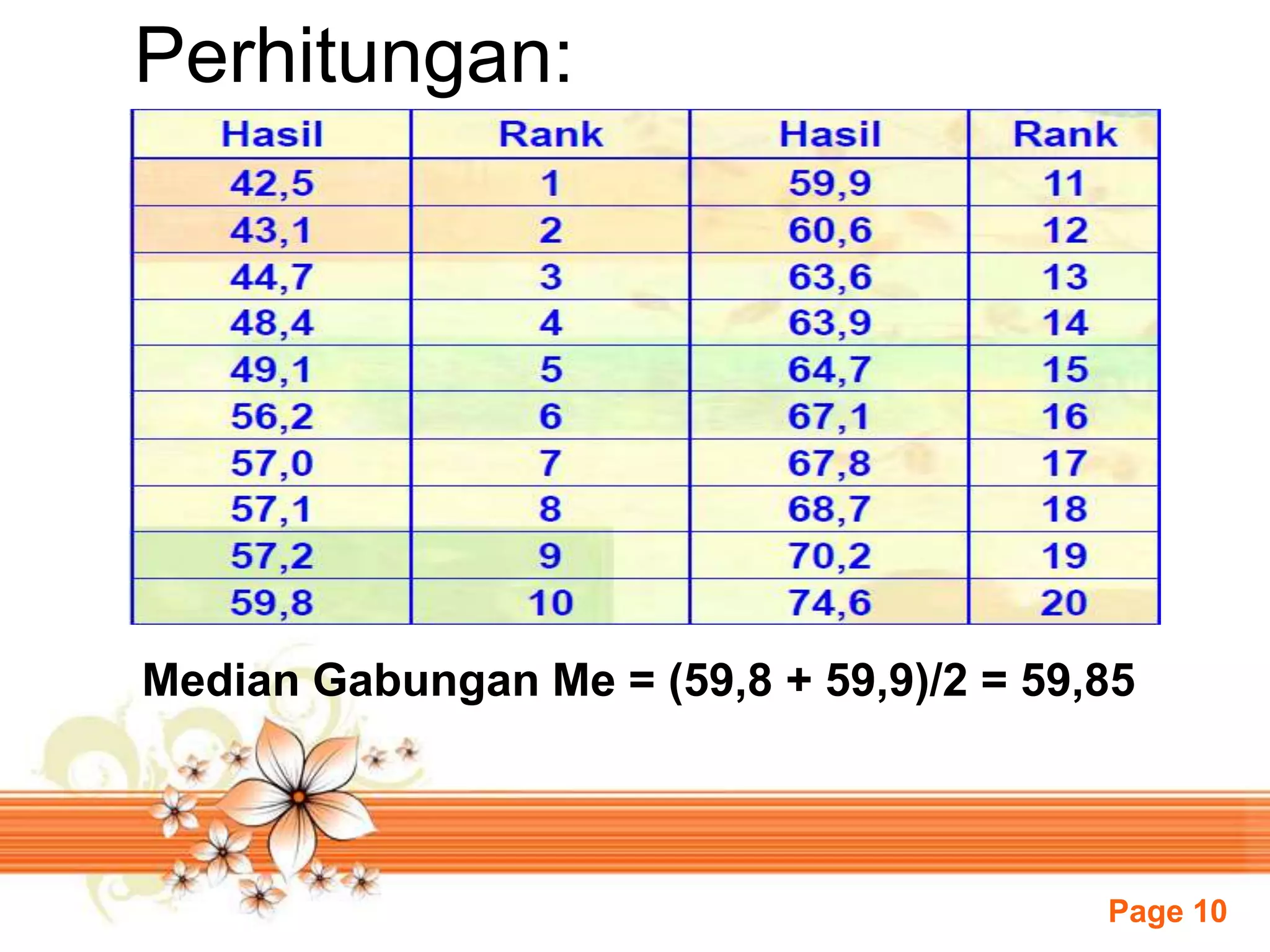
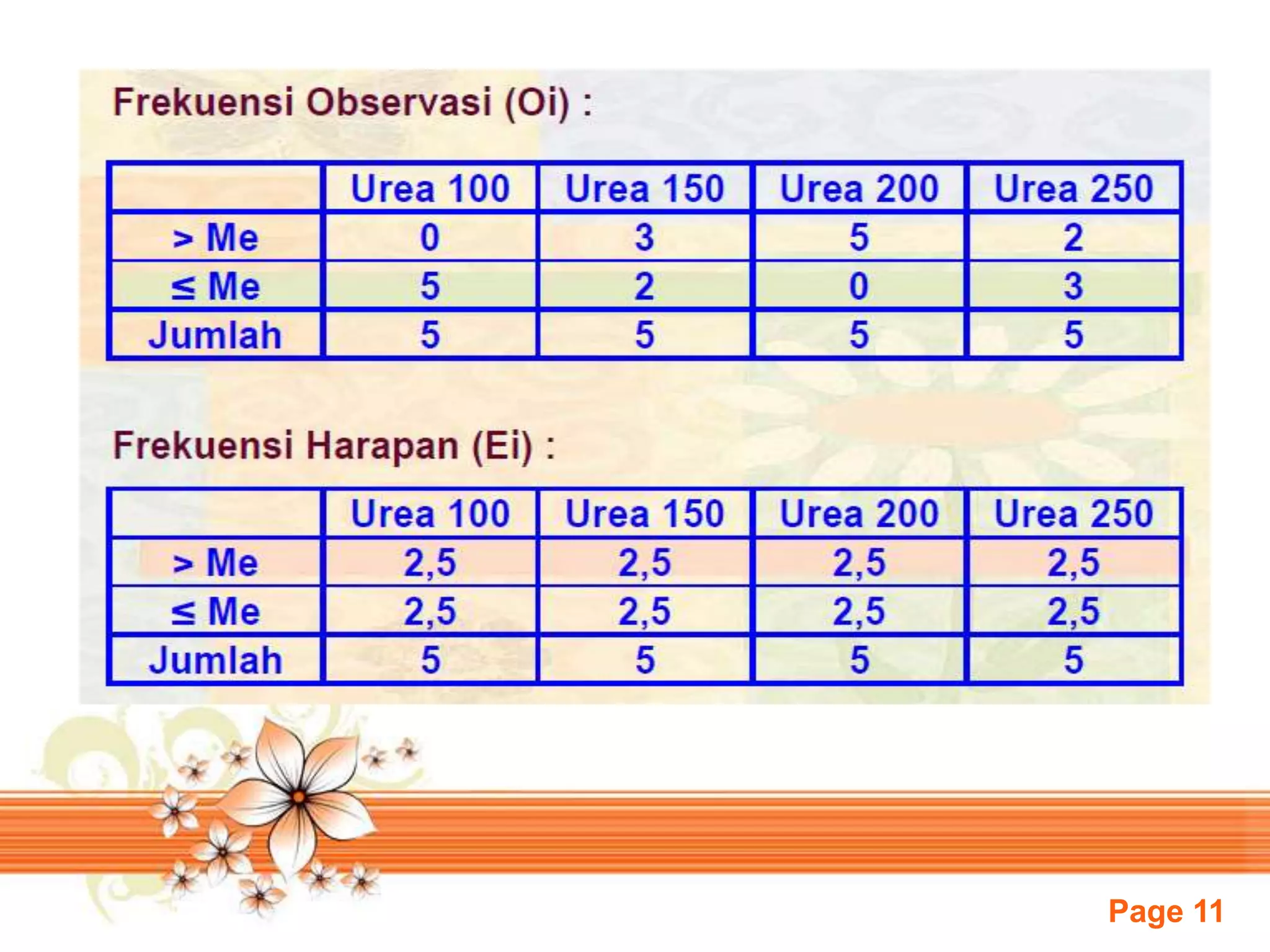
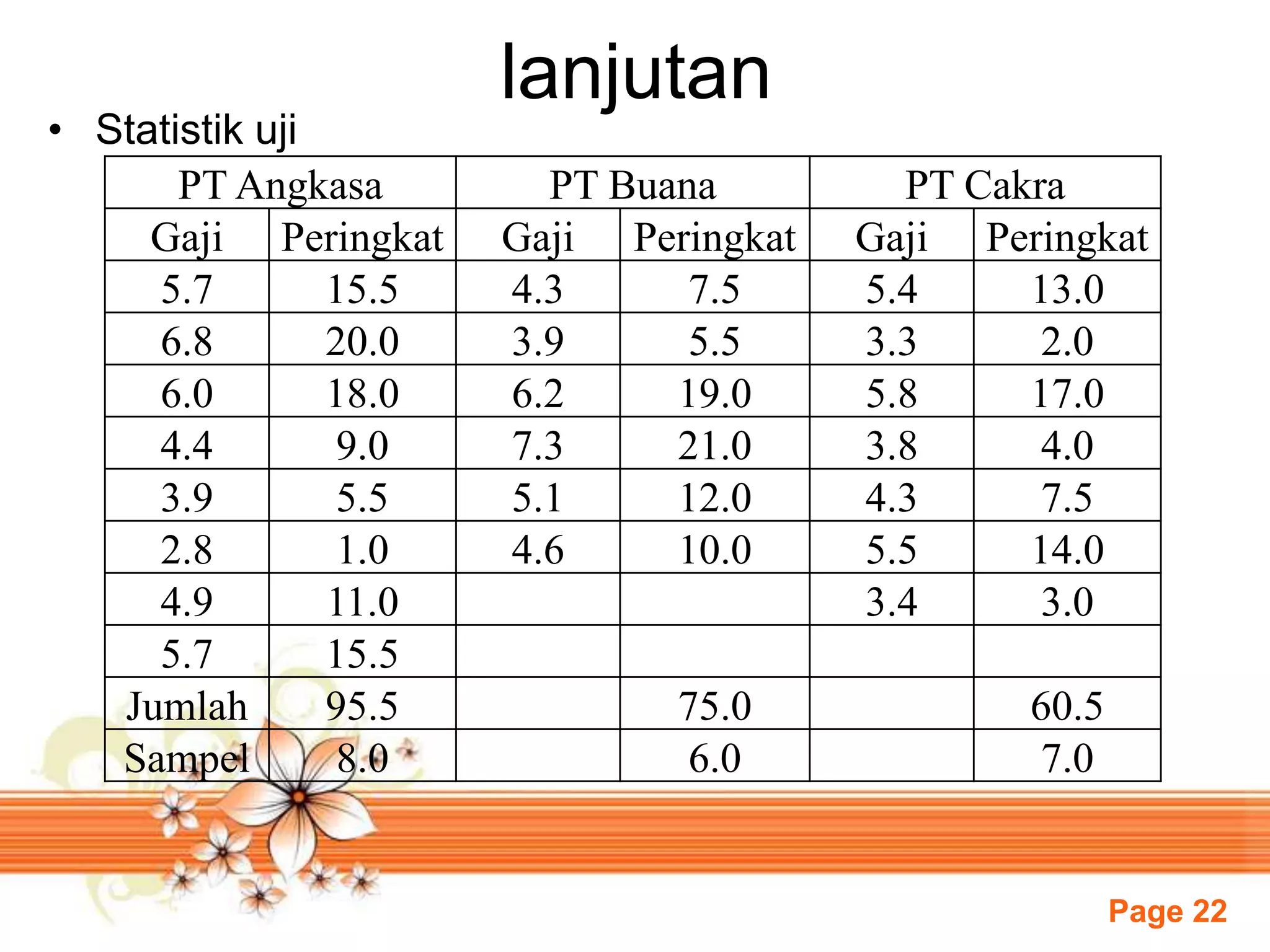
Dokumen ini membahas uji statistik untuk sampel independen, khususnya uji median dan uji Kruskal-Wallis. Uji median digunakan untuk menguji apakah beberapa populasi memiliki median yang sama, sedangkan uji Kruskal-Wallis merupakan perluasan dari uji jumlah rank untuk menguji apakah sampel berasal dari populasi yang sama. Dokumen ini juga memberikan contoh soal uji median dan uji Kruskal-Wallis beserta langkah penger