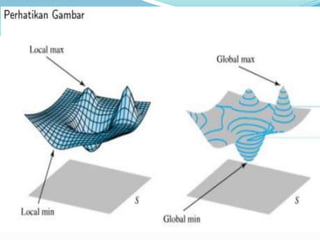
Dokumen ini membahas konsep nilai ekstrim global dan lokal dari fungsi dalam ruang dua dimensi, serta teorema yang berkaitan dengan eksistensi nilai maksimum dan minimum. Titik kritis ditentukan oleh titik batas, titik stasioner, dan titik singular, yang berpotensi menjadi lokasi ekstrim. Terdapat juga kriteria untuk menentukan sifat lokal maksimum atau minimum menggunakan turunan parsial kedua.

2. Nilai Ekstrim Global
Misalkan S ⊆ 𝑅2, 𝑓 ∶ 𝑆 → 𝑅, 𝑑𝑎𝑛 𝑝0 ∈ 𝑆
i. 𝑓(𝑝0) disebut nilai maksimum global 𝑓 pada S apabila 𝑓 𝑝 𝑜 ≥
𝑓 𝑝 untuk setiap 𝑝 ∈ 𝑆.
ii. 𝑓(𝑝0) disebut nilai minimum global 𝑓 pada 𝑆 apabila 𝑓 𝑝0 ≤
𝑓 𝑝 untuk setiap 𝑝 ∈ 𝑆.
Nilai 𝑓(𝑝0) disebut Nilai Ekstrim Global 𝑓 pada 𝑆 apabila 𝑓(𝑝0)
merupakan nilai maksimum g;obal atau nilai minimum global.
Definition (Nilai Ekstrim Global)

3. Nilai Ekstrim Lokal
Misalkan 𝑆 ⊆ 𝑅2, 𝑓 ∶ 𝑆 → 𝑅, dan 𝑝0 ∈ 𝑆
i. 𝑓(𝑝0) disebut nilai maksimum lokal 𝑓 pada 𝑆 apabila
terdapat cakram 𝑁 yang memuat 𝑝0 sehingga
𝑓 𝑝0 ≥ 𝑓(𝑝0) untuk setiap 𝑝 ∈ 𝑁 ∩ 𝑆.
ii. 𝑓(𝑝0) disebut nilai minimum lokal 𝑓 pada 𝑆 apabila
terdapat cakram 𝑁 yang memuat 𝑝0 sehingga
𝑓 𝑝0 ≤ 𝑓(𝑝0) untuk setiap 𝑝 ∈ 𝑁 ∩ 𝑆.
Nilai 𝑓(𝑝0) disebut nilai ekstrim lokal 𝑓 pada 𝑆 apabila
𝑓(𝑝0) merupakan nilai maksimum lokal atau minimum
lokal.

5. Theorem (Eksistensi Maks-Min)
Jika f kontinu pada suatu himpunan tertutup dan
terbatas S, maka f mencapai nilai maksimum dan
nilai minimum global pada S (kemungkinan di
titik yang berbeda).
Catatan:
S tertutup bertarti S memuat titik-titik
perbatasannya. S terbatas berarti S termuat
dalam suatu cakram ∁ (O,R) yang berpusat di O
(0,0) dan berjari-jari R, untuk suatu R > 0.

6. Theorem (Titik Kritis)
Fungsi f hanya mungkin mencapai nilai ekstrim pada titik-
titik kritis, yaitu:
i. Titik-titik perbatasan 𝑑𝑎𝑒𝑟𝑎ℎ 𝑎𝑠𝑎𝑙 𝑓, 𝑎𝑡𝑎𝑢
ii. Titik-titik stasioner
𝑦𝑎𝑖𝑡𝑢 𝑡𝑖𝑡𝑖𝑘 𝑑𝑖𝑚𝑎𝑛𝑎 𝑓 𝑚𝑒𝑚𝑝𝑢𝑛𝑦𝑎𝑖 𝑡𝑢𝑟𝑢𝑛𝑎𝑛 0 , 𝑎𝑡𝑎𝑢
iii. Titik-titik singular
𝑦𝑎𝑖𝑡𝑢 𝑡𝑖𝑡𝑖𝑘 𝑑𝑖𝑚𝑎𝑛𝑎 𝑓 𝑡𝑖𝑑𝑎𝑘 𝑚𝑒𝑚𝑝𝑢𝑛𝑦𝑎𝑖 𝑡𝑢𝑟𝑢𝑛𝑎𝑛 .

7. Catatan:
Titikstasionerbelumtentumerupakantitikekstrim.
Sebagaicontoh, fungsi 𝑓 (𝑥, 𝑦 ) =
𝑥𝑦 mempunyaititikstasioner (0, 0),
tetapititikinibukanmerupakantitikekstrim (global
maupunlokal). Ingatpetakonturnyasepertiapa!
Jikadaerahasalfungsi f dibatasipadacakramtertutup
C(O, 1), makanilaiekstrimnyahanyamungkintercapai di
titik-titikperbatasan, yaitupadalingkaran 𝑥 2 + 𝑦2 =
1.

8. Syarat Cukup Nilai Ekstrim
Theorem (UjiParsialKedua)
Misalkan 𝑓 𝑥, 𝑦 mempuyaiturunanparsialkedua yang
kontinupadasuatucakram yang berpusat di (a, b)
dan𝛻𝑓 𝑎, 𝑏 = 0, 0 . 𝑇𝑢𝑙𝑖𝑠
𝐷 = 𝐷 𝑎, 𝑏 = 𝑓𝑥𝑥 𝑎, 𝑏 . 𝑓𝑦𝑦 (𝑎, 𝑏) [𝑓𝑥𝑦 (𝑎, 𝑏)]
Maka
 Jika𝐷 > 0 dan𝑓𝑥𝑥 (𝑎, 𝑏) < 0maka f (a, b)
merupakannilaimaksimum local
 Jika𝐷 > 0 dan𝑓𝑥𝑥 (𝑎, 𝑏) > 0maka f (a, b) merupakannilai
minimum local
 Jika 𝐷 < 0, maka (a, b) merupakantitikpelanadan f (a, b)
bukantitikekstrim

9. " Terima Kasih, Semoga bermanfaat "