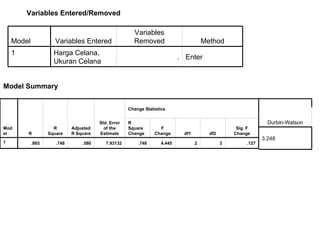
The document discusses linear regression analysis that was performed to develop a regression equation to predict clothing price based on weight and clothing size. It provides the regression outputs, including the regression equation with an intercept of 74.42 and slope of 2.44 for predicting price based on weight, and an equation with an intercept of -1.355 and slope of 0.566 for predicting price based on size. Tables show the descriptive statistics, model summary, residuals statistics and sums of squares and cross products from the regression analysis.

1. REGRESI KELOMPOK 4: ARMAN FERNANDO. S DETTI APRIANI ENI INDRIATI

2. DEFINISI REGRESI # Menurut Sir Francis Galton (1822-1911) Persamaan Regresi :Persamaan matematik yang memungkinkan peramalan nilai suatu peubah takbebas ( dependent variable ) dari nilai peubah bebas (independent variable). Jenis-jenis Persamaan Regresi : Regresi Linier : Regresi Linier Sederhana & Regresi Linier Berganda Regresi Nonlinier Regresi Eksponensial - Bentuk Umum Regresi Linier Sederhana Y = a + bX Y : peubah takbebas X : peubah bebas a : konstanta b : kemiringan

5. Data hasil pengamatan Regresi ∑ y= 306 ∑ x2= 555 ∑ x1= 183 68 125 38 T 6 60 100 33 S 5 40 90 29 R 4 55 85 28 Q 3 47 85 28 P 2 36 70 27 O 1 Berat Badan Harga Celana (puluh ribuan) Ukuran Celana NAMA NO.

6. Regression Descriptive Statistics 6 18.64135 92.5000 Harga Celana 6 4.23084 30.5000 Ukuran Celana 6 12.23111 51.0000 Berat Badan N Std. Deviation Mean

7. Variables Entered/Removed Model Summary Enter . Harga Celana, Ukuran Celana 1 Method Variables Removed Variables Entered Model 3.248 Durbin-Watson .127 3 2 4.445 .748 7.93132 .580 .748 .865 1 Sig. F Change df2 df1 F Change R Square Change Change Statistics Std. Error of the Estimate Adjusted R Square R Square R Model

9. Residuals Statistics 6 .254 .333 .690 .168 Centered Leverage Value 6 .662 .460 1.784 .001 Cook's Distance 6 1.270 1.667 3.451 .842 Mahal. Distance 6 1.289 -.163 1.694 -2.059 Stud. Deleted Residual 6 12.53070 -3.5050 12.9319 -19.8228 Deleted Residual 6 1.028 -.118 1.329 -1.428 Stud. Residual 6 .775 .000 1.084 -1.159 Std. Residual 6 6.14357 .0000 8.5978 -9.1957 Residual 6 11.64868 54.5050 75.7143 42.0681 Adjusted Predicted Value 6 1.35073 5.47106 7.34186 4.59157 Standard Error of Predicted Value 6 1.000 .000 1.755 -1.150 Std. Predicted Value 6 10.57622 51.0000 69.5652 38.8370 Predicted Value N Std. Deviation Mean Maximum Minimum

10. Charts

12. ∑ Y²= 16354 ∑ (X2)²= 53075 ∑ (x1)²= 5671 ∑ x2= 29290 ∑ x1y= 9552 ∑ y= 306 ∑ x2= 555 ∑ x1= 183 4624 15625 1444 8500 2584 68 125 38 T 6 3600 10000 1089 6000 1980 60 100 33 S 5 1600 8100 841 3600 1160 40 90 29 R 4 3025 7225 784 4675 1540 55 85 28 Q 3 2209 7225 784 3995 1316 47 85 28 P 2 1296 4900 729 2520 972 36 70 27 O 1 Y² (X2)² (x1)² x2y x1y Y x2 x1 NAMA NO.

13. b= (6 X 9552) - (183)(306) (6 X 5671) - (183)² = 1314 537 = 2,44 a= (306:6) – (2,44 X (183 : 6)) = 51 – (- 23,42) = 51+ 23,42 = 74,42 Y= 74,42 + 2,44x

14. b= (6 X 29290) - (555)(306) (6 X 53075) - (555) = 5910 10425 = 0, 566 a= (306:6) – (0,566 X (555 : 6)) = 51 – (52,355) = -1,355 Y= 0,566 – 1,355x