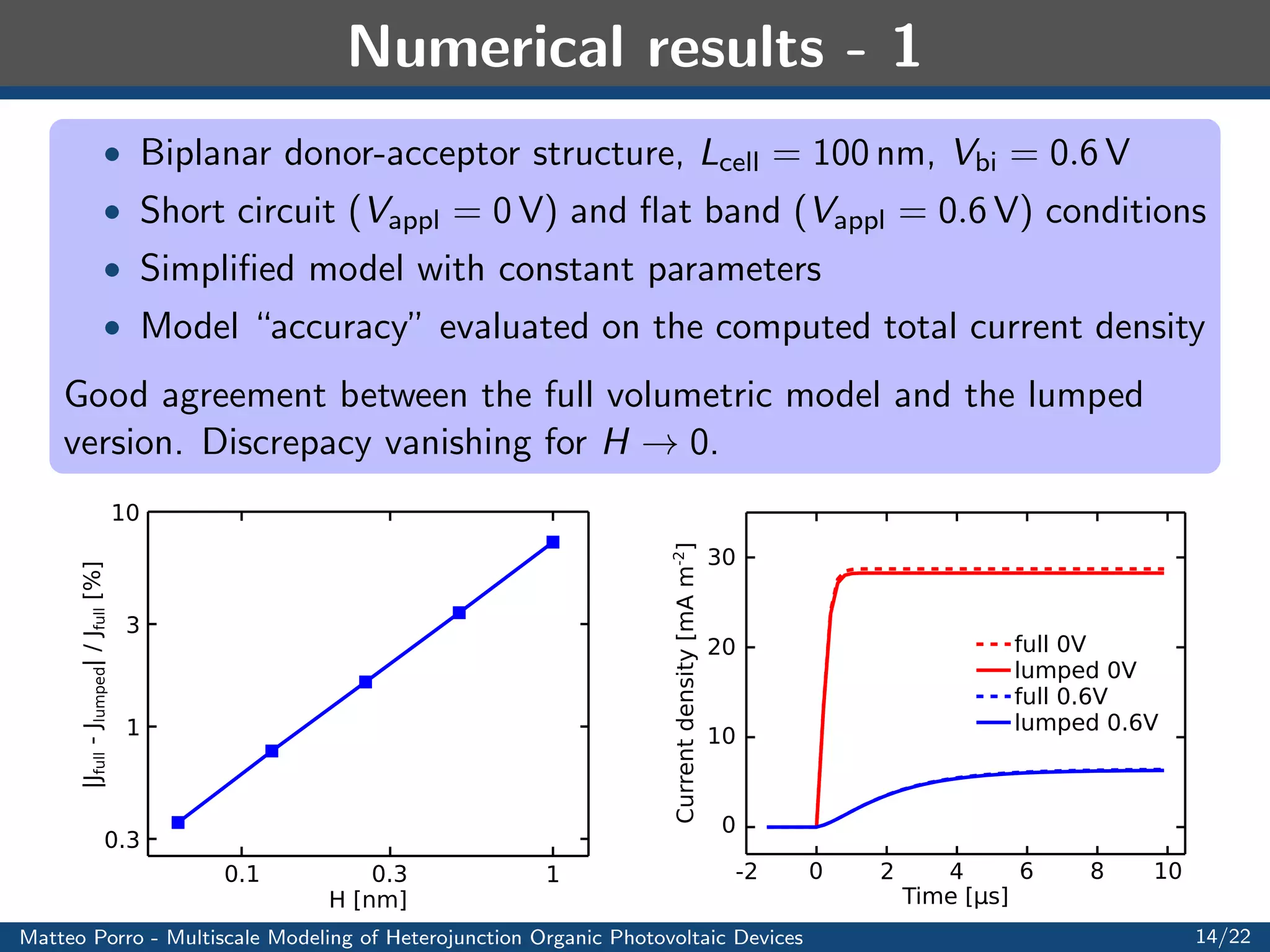
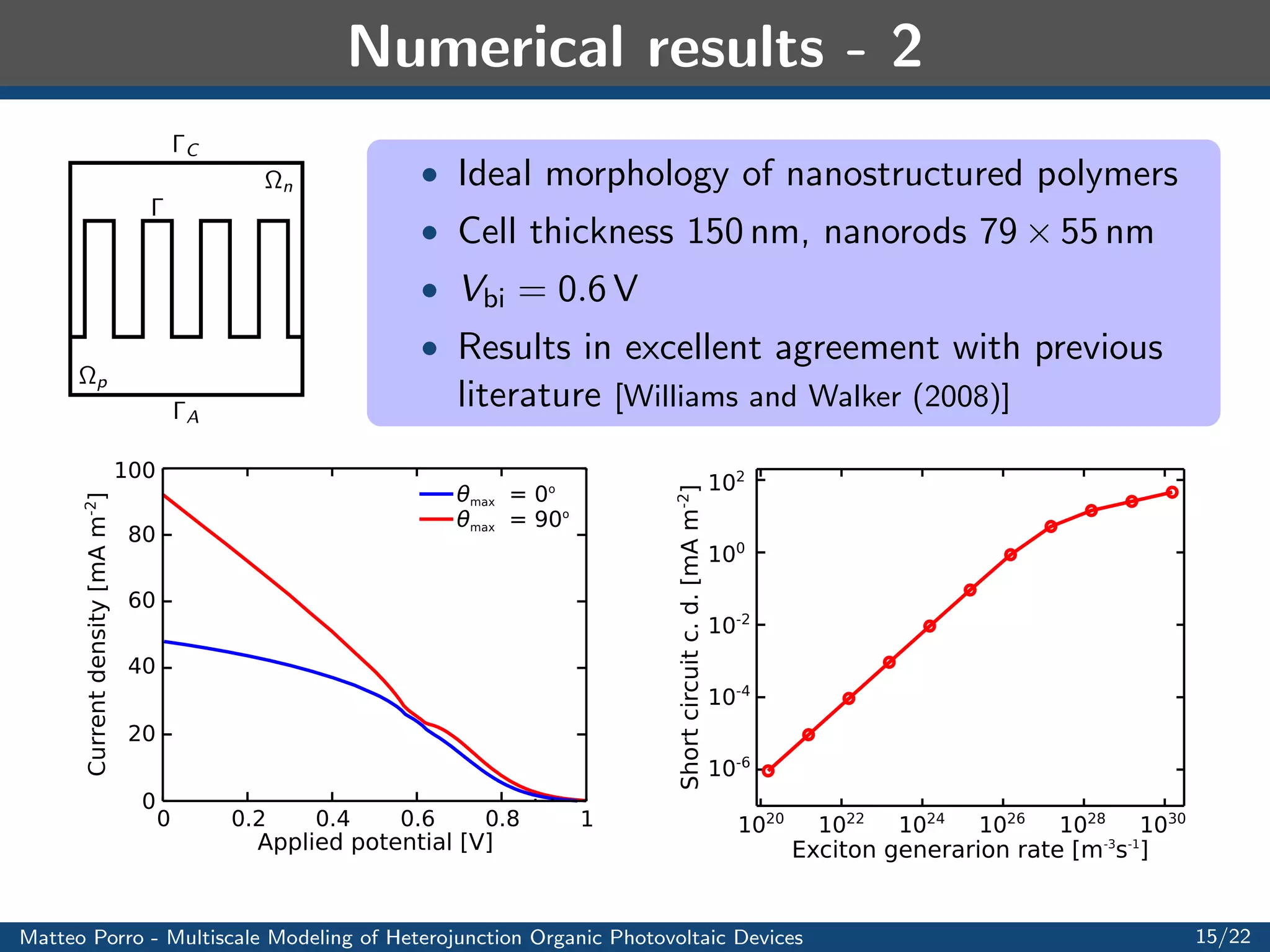
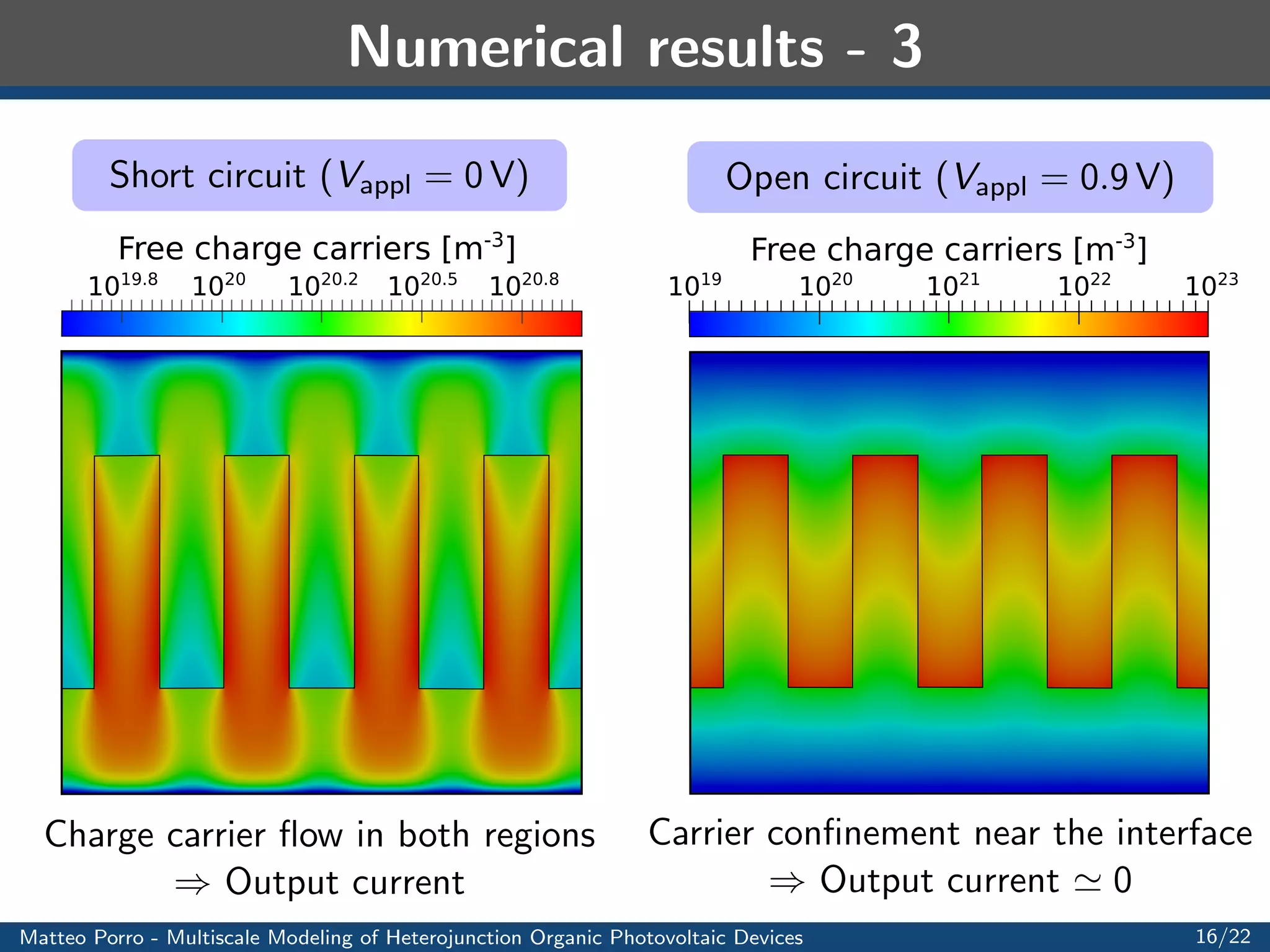
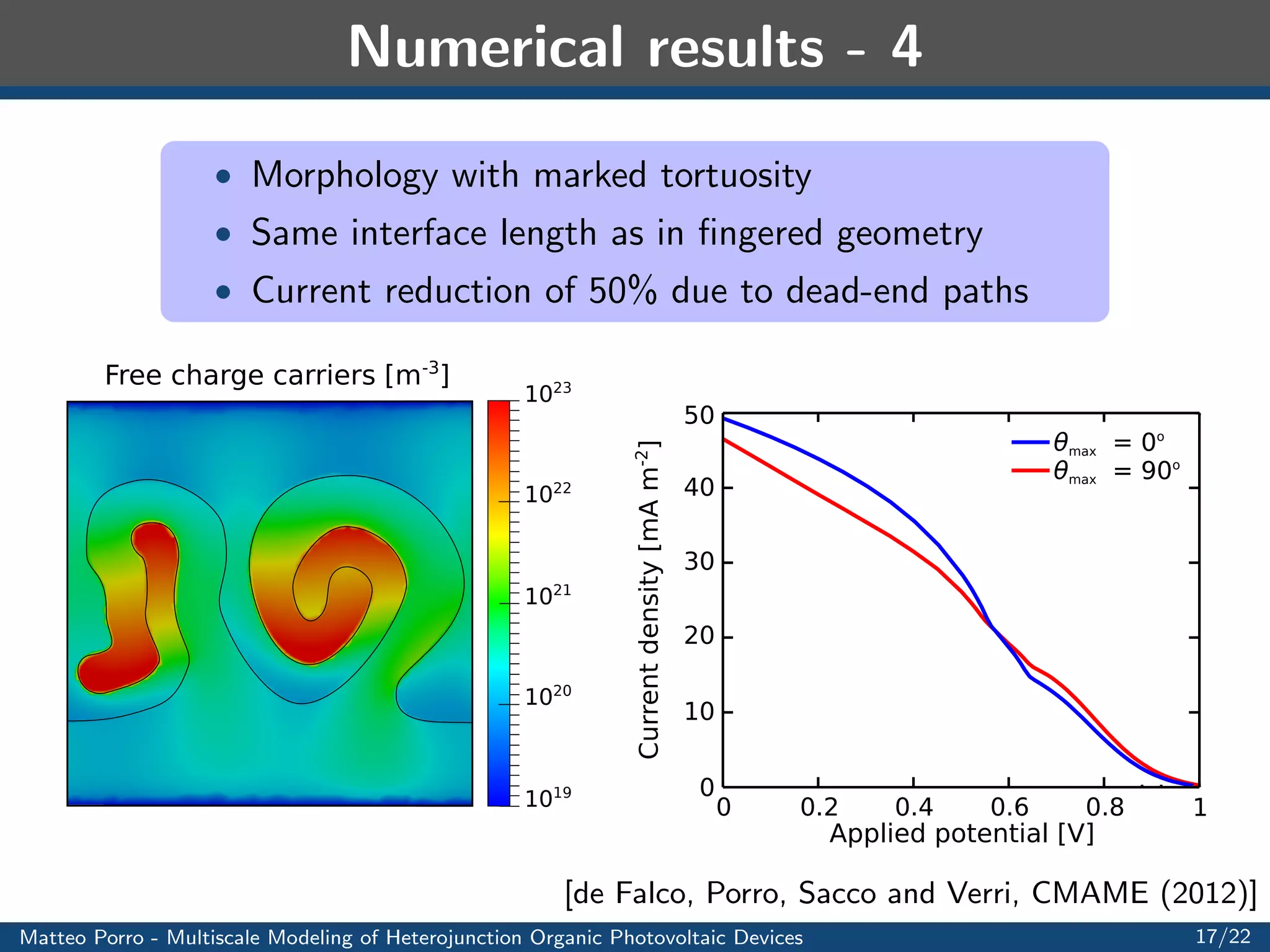
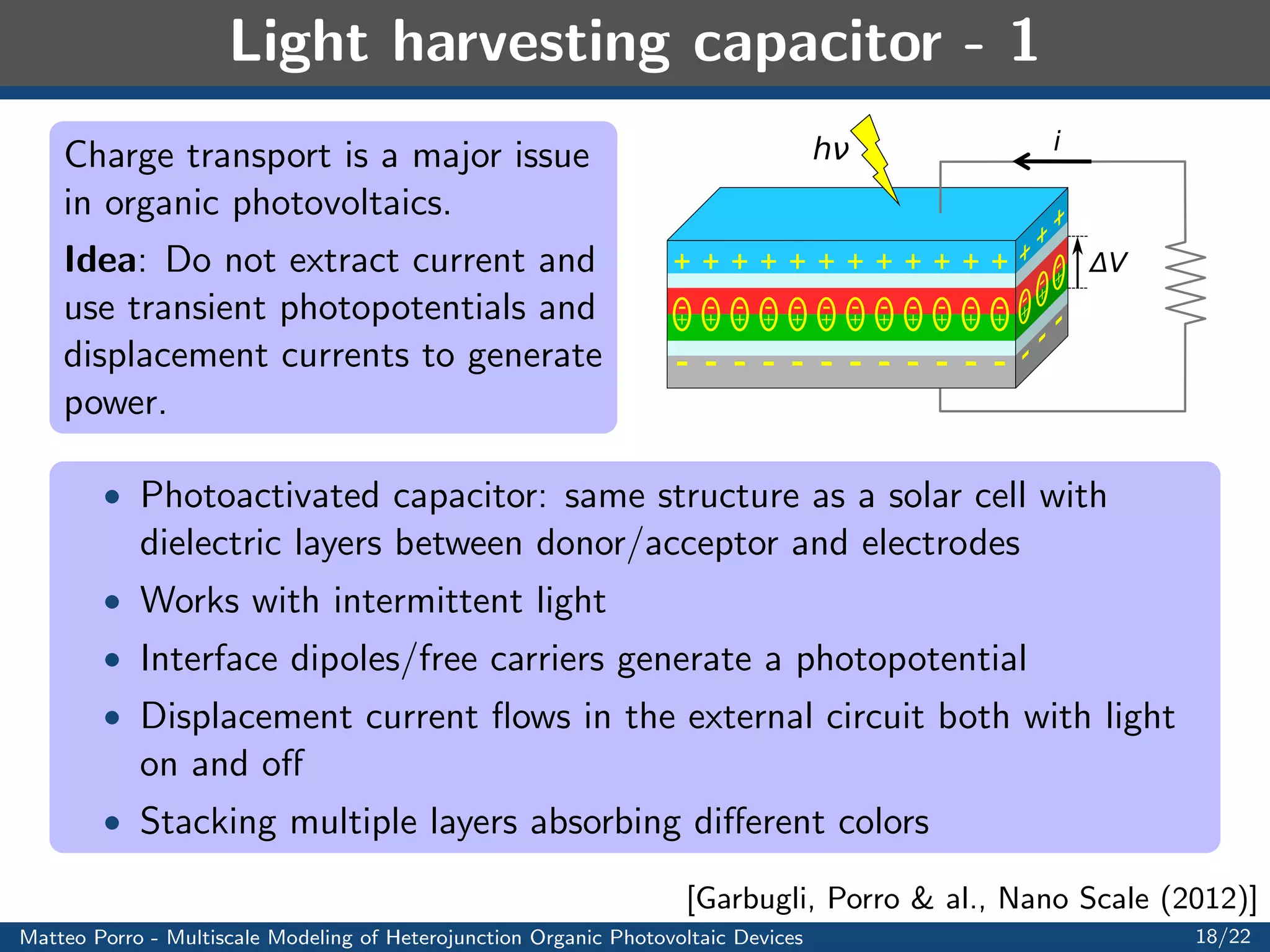
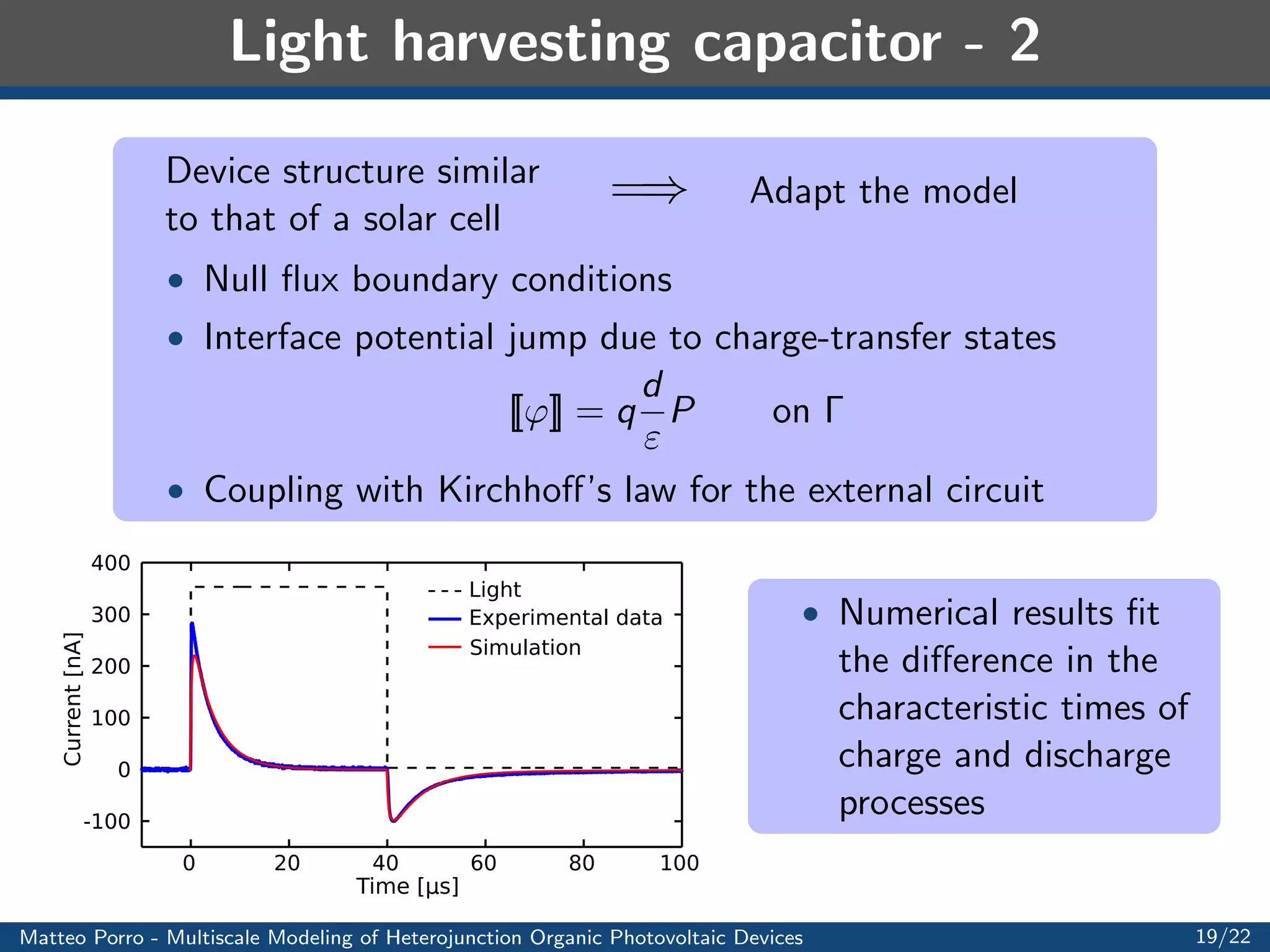
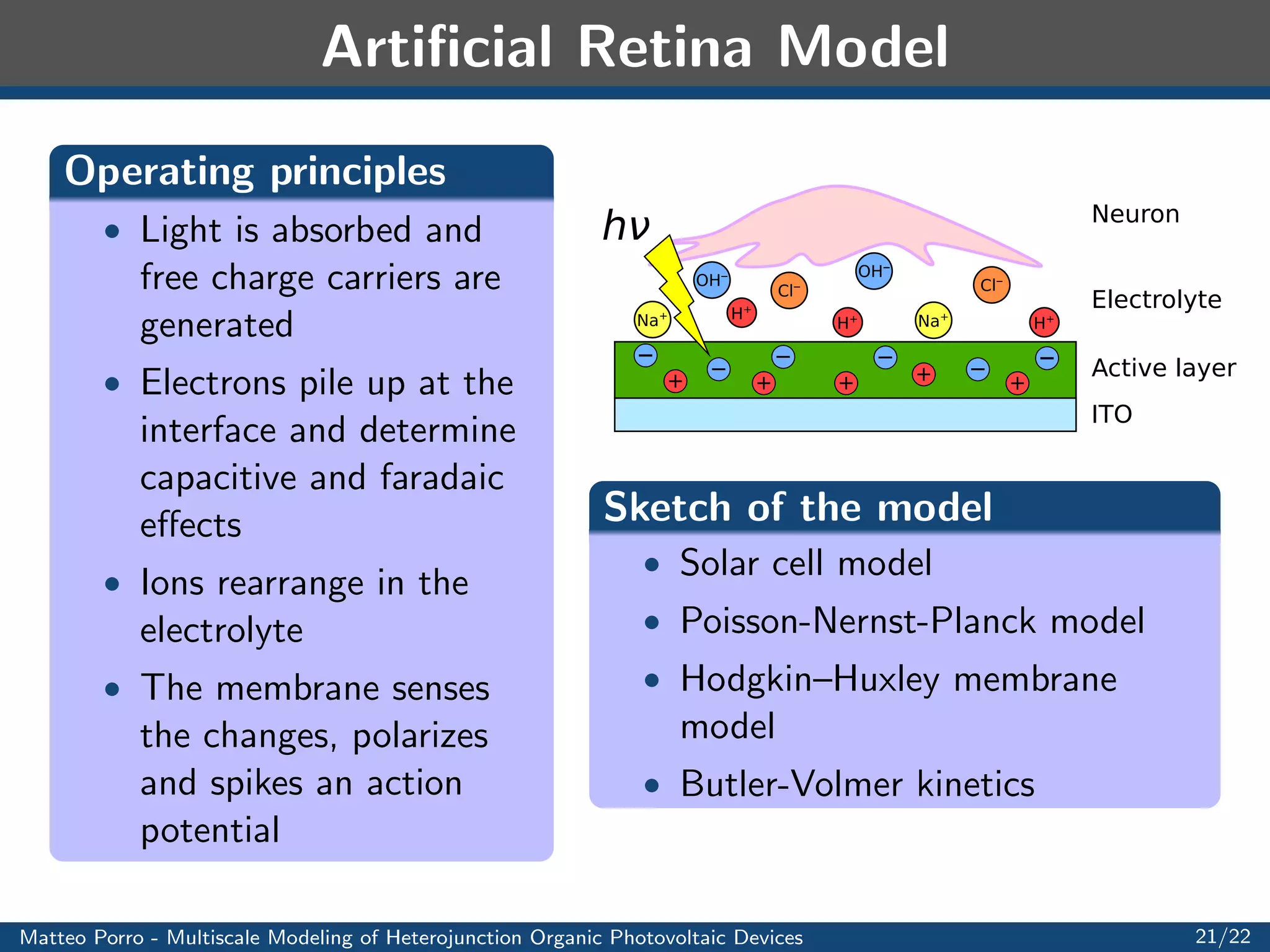
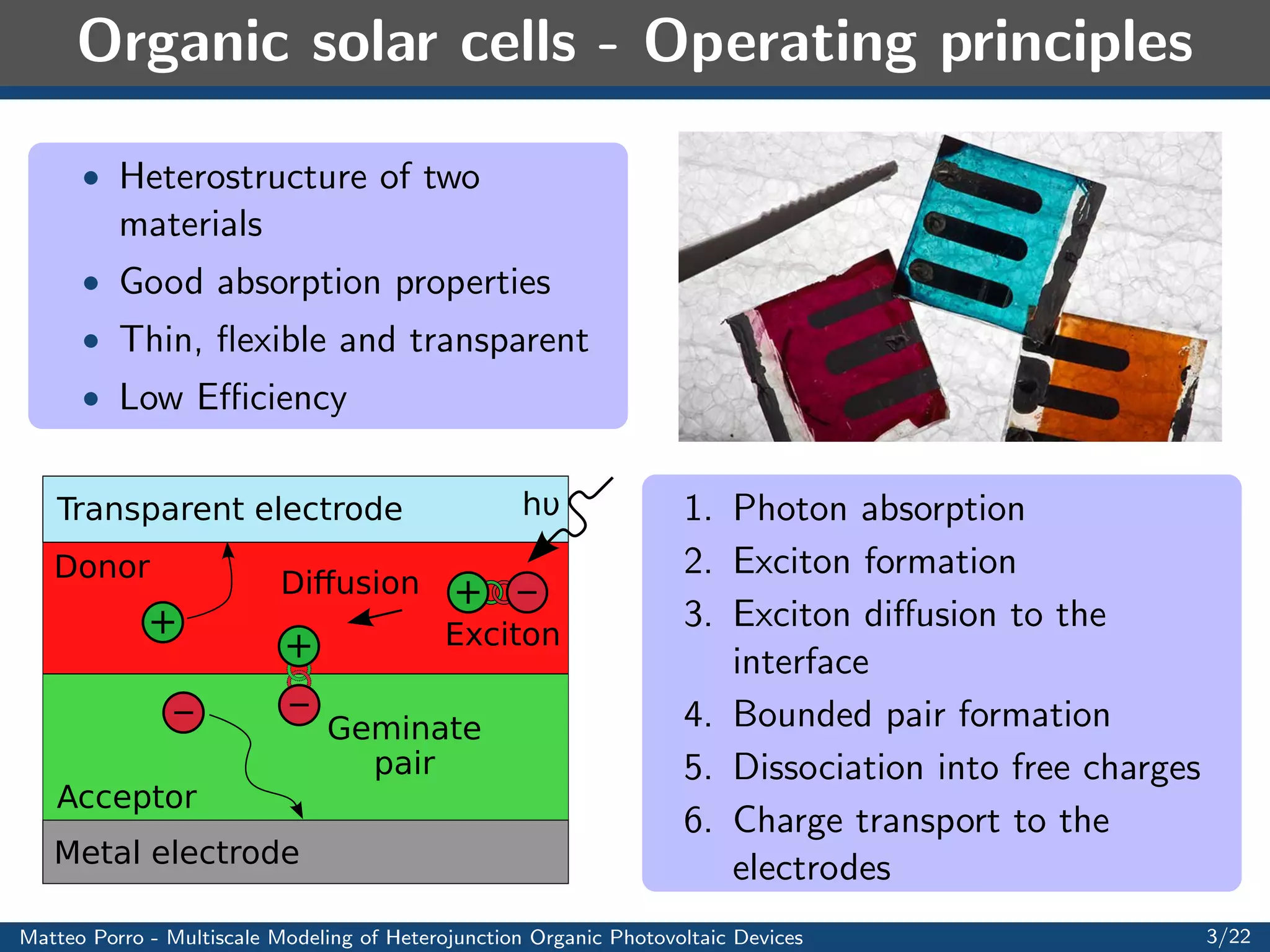
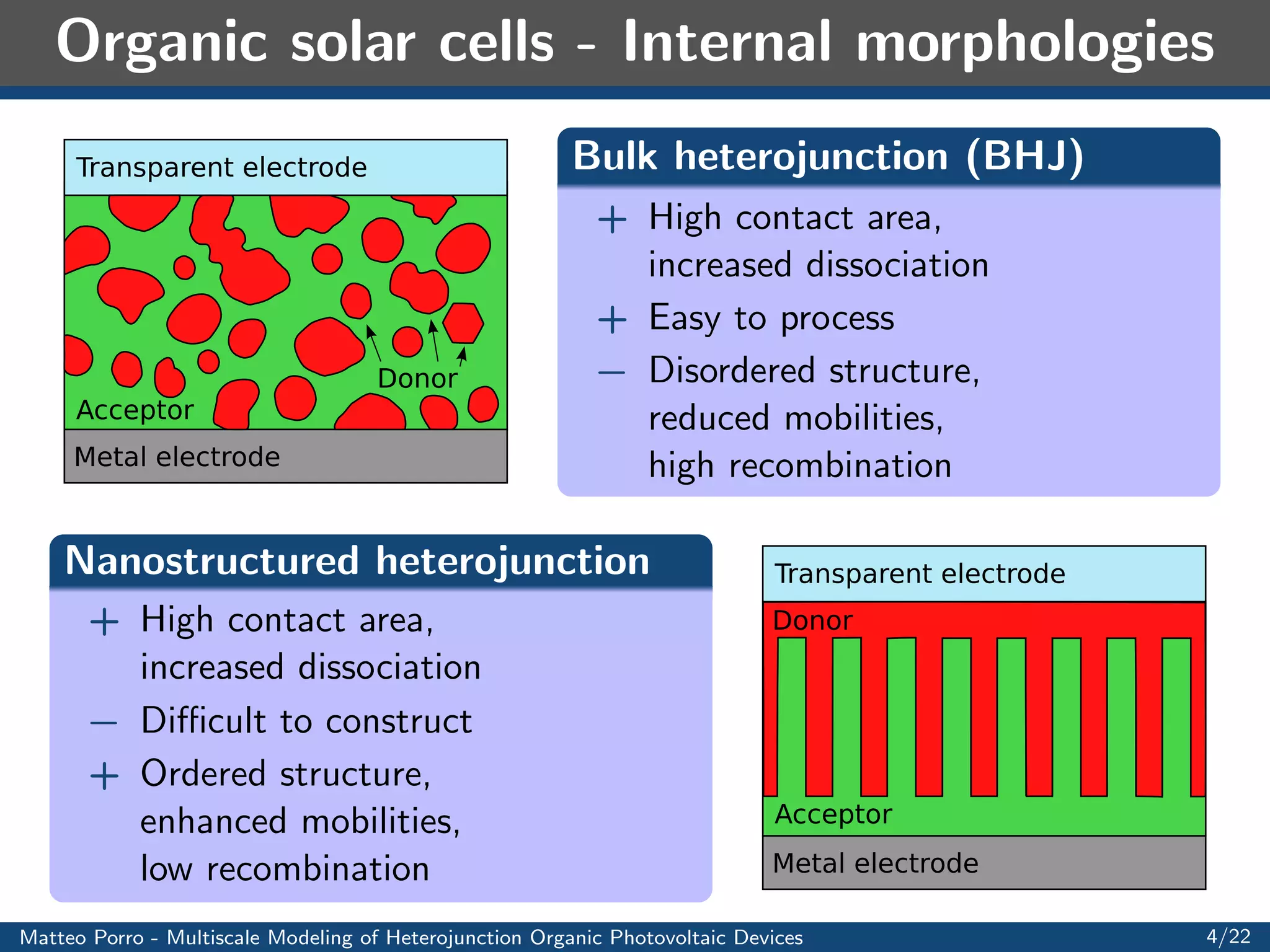
This document summarizes a presentation on multiscale modeling of organic photovoltaic devices. It discusses the operating principles of organic solar cells and their internal morphologies. It then presents the mathematical model developed, which uses a multiscale approach to model exciton transport and dissociation, charge transport, and the electric field. Numerical results are shown applying the model to different device structures, demonstrating the effects of morphology on performance. Applications to light harvesting capacitors and artificial retinas are also discussed.

1. MSH 2012 - Mathematics for Semiconductor Heterostructures
Berlin - September 27, 2012
Multiscale Modeling of Heterojunction
Organic Photovoltaic Devices
Matteo Porro
Dipartimento di Matematica Francesco Brioschi"
Politecnico di Milano, Italy
Center for Nano Science and Technology @PoliMi
Istituto Italiano di Tecnologia, Italy
email: matteo.porro@mail.polimi.it
web: www1.mate.polimi.it/porro

2. Summary
Organic solar cells - A brief introduction
Mathematical model and multiscale approach
Numerical results
Beyond OSCs - Light harvesting capacitor and
arti

3. cial retina
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 2/22

4. Organic solar cells - Operating principles
Heterostructure of two
materials
Good absorption properties
Thin,
exible and transparent
Low Eciency
Transparent electrode
Donor
Acceptor
+
Metal electrode
+
hυ 1. Photon absorption
_
_
+
_
Di usion
Geminate
pair
Exciton
2. Exciton formation
3. Exciton diusion to the
interface
4. Bounded pair formation
5. Dissociation into free charges
6. Charge transport to the
electrodes
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 3/22

5. Organic solar cells - Internal morphologies
Transparent electrode
Acceptor
Metal electrode
Donor
Bulk heterojunction (BHJ)
+ High contact area,
increased dissociation
+ Easy to process
Disordered structure,
reduced mobilities,
high recombination
Nanostructured heterojunction
+ High contact area,
increased dissociation
Dicult to construct
+ Ordered structure,
Transparent electrode
Donor
Acceptor
enhanced mobilities,
low recombination Metal electrode
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 4/22

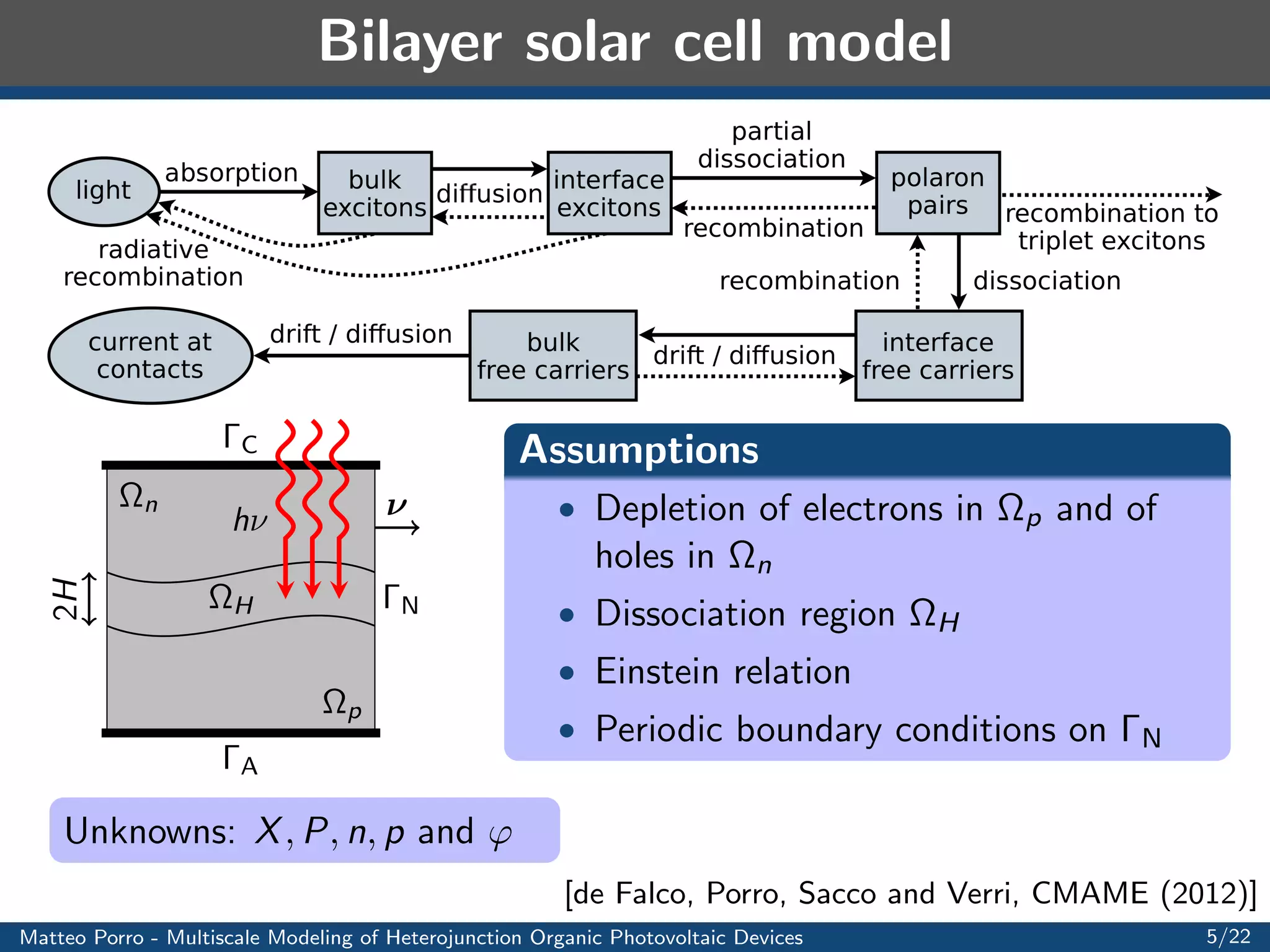
6. Bilayer solar cell model
absorption
di
C
h
n
p
H
A
N
2H
Assumptions
Depletion of electrons in
p and of
holes in
n
Dissociation region
H
Einstein relation
Periodic boundary conditions on N
Unknowns: X; P; n; p and '
[de Falco, Porro, Sacco and Verri, CMAME (2012)]
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 5/22

7. Multiscale modeling - Interface lumping
Device thickness active layer thickness
( 102/ 100 nm)
Despite this, a re

8. ned mesh size is needed
to accurately describe phenomena in
H
Idea
Neglect the thickness of the active layer
Assume the phenomena to occur just on the
mathematical interface
C
h
n
N N
p
A
New computational
domain
Many nodes
Less nodes
Good resolution
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 6/22

9. Model equations - 1
Exciton
equation
8
:
@X
@t
+ div JX = G
X
X
in
n [
p
@X
@t
+ div JX = G
X
X
X
diss
+ krecP in
H
JX = DXrX in
X = 0 on C [ A
X(x; 0) = X0(x) in
Excitons have null net charge ! Just diusion (Fick's law)
Generation term G(x; t): constant, Beer-Lambert
Exciton lifetime X , geminate pair formation time diss
Geminate pair recombination rate constant krec and triplet
exciton fraction
X and the normal component of JX are continuous in
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 7/22

10. Model equations - Lumping procedure
Extend the validity of the bulk continuity equation to
n with
interface conditions
[[X]] = 0 and [[JX ]] = H
X on
Interface source term H
X obtained with a lumping operation
H
X =
ZH
H
krecP
X
diss
d = krec
ZH
H
P d
1
diss
ZH
H
X d ' kreceP
2H
diss
Xj
Exciton
equation
8
:
@X
@t
+ div JX = G
X
X
in
n [
p =
n
eP
JX = DXrX in
[[X]] = 0 on
[[JX ]] = krec
2H
diss
X on
X = 0 on C [ A
X(x; 0) = X0(x) in
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 8/22

11. Model equations - 2
Geminate pair
equation
8
:
@eP
@t
=
2H
diss
X (kdiss + krec)eP
+ 2H
np on
eP
= 0 in
n
eP
(x; 0) = eP0(x) in
Novel model for the dissociation rate constant kdiss(E)
Langevin bimolecular recombination
np
Electron
equation
(Hole equation is
analogous)
8
:
@n
@t
1
q
div Jn = 0 in
n
eP
Jn = qDnrn qnnr' in
n
1
Jn = kdiss 2H
np on
q
n
1
q
Jn + nn =

12. n on C
n(x; 0) = n0(x) in
n
n = 0 in
p
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 9/22

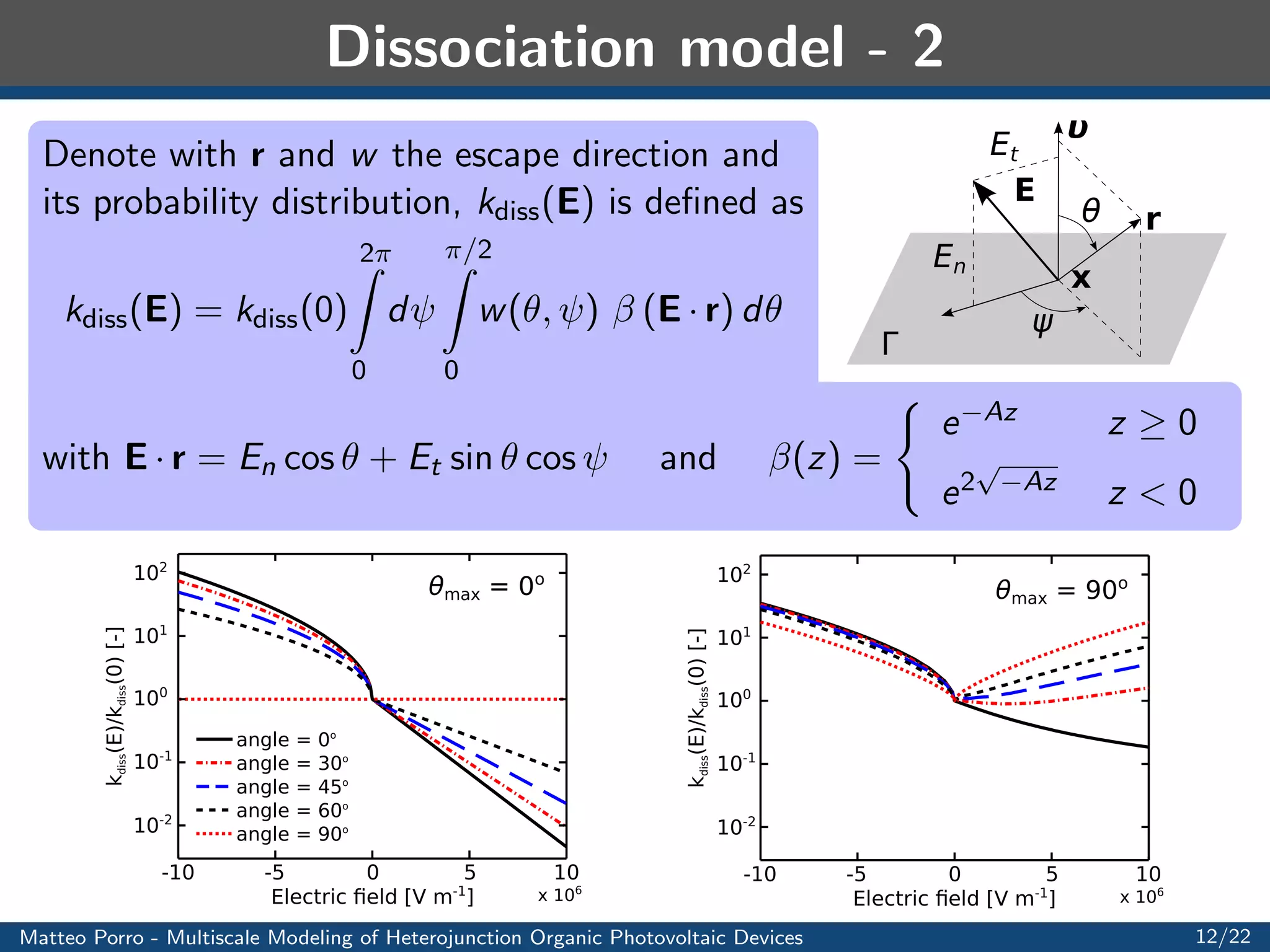
13. Model equations - 3
Poisson
equation
8
:
div
r'
= qn in
n
div
r'
= +qp in
p
[[']] = [[r' ]] = 0 on
' = Vappl Vbi on A
' = 0 on C
Fixed potential at the electrodes (applied and built-in potential)
! Dirichlet boundary conditions
The dielectric constant may vary in the materials
The electric potential ' and the normal component of the electric
displacement

14. eld D = r' are continuous
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 10/22

15. Dissociation model - 1
Several approaches in literature
Braun-Onsager model. Homogeneity assumption. Just electric

16. eld magnitude is taken into account.
Barker-Ramsdale-Greenham. Electric

17. eld orientation on planar
devices. Averaging over a range of admissible escape angles.
Williams-Walker. Apply BRG model to arbitrary geometries by
averaging along the interface the normal component of the

18. eld.
Transparent electrode
Donor
+ _
_
Acceptor
Metal electrode
+
_
+
E
E
d
d
E d
Idea
Proceed as in BRG model,
removing the hypothesis of
electric

19. eld E normal to the
interface
(d is the electric dipole)
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 11/22

20. Dissociation model - 2
Denote with r and w the escape direction and
its probability distribution, kdiss(E) is de

21. ned as
kdiss(E) = kdiss(0)
Z2
0
d
Z=2
0
w(; )

22. (E r) d
Γ
ψ
υ
θ
Et
E
En
r
x
with E r = En cos + Et sin cos and

23. (z) =
(
eAz z 0
p
e2
Az z 0
102
101
[-]
0) (diss100
kE)/angle = 0o
(diss10-1
angle = 30o
kangle = 45o
angle = 60o
10-2
angle = 90o θmax = 0o
-10 -5 0 5 10
Electric eld [V m-1] x 106
102
101
100
-10 -5 0 5 10
kdiss(E)/kdiss(0) [-]
Electric eld [V m-1] x 106
10-1
10-2
θmax = 90o
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 12/22

24. Numerical approach
The problem and its constraints
Fully coupled system Strongly nonlinear equations
Avoid negative concentrations, also to prevent instabilities and
numerical oscillation in the iterative solution algorithm
Rothe's method
Time discretization with an adaptive BDF method
Problem linearization with a quasi-Newton method
Spatial discretization with SG exponentially

25. tted FEs
Numerical implementation of 1D/2D versions of the model with the
open source tool GNU Octave.
Light-weight simulations: O(min).
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 13/22

26. Numerical results - 1
Biplanar donor-acceptor structure, Lcell = 100 nm, Vbi = 0:6 V
Short circuit (Vappl = 0 V) and
at band (Vappl = 0:6 V) conditions
Simpli

27. ed model with constant parameters
Model accuracy evaluated on the computed total current density
Good agreement between the full volumetric model and the lumped
version. Discrepacy vanishing for H ! 0.
0.1 0.3 1
H [nm]
|Jfull - Jlumped| / Jfull [%]
10
3
1
0.3
full 0V
lumped 0V
full 0.6V
lumped 0.6V
30
20
10
-2 0 2 4 6 8 10
Time [ s]
0
Current density [mA m-2]
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 14/22

28. Numerical results - 2
n
p
C
A
Ideal morphology of nanostructured polymers
Cell thickness 150 nm, nanorods 7955 nm
Vbi = 0:6 V
Results in excellent agreement with previous
literature [Williams and Walker (2008)]
θmax = 0o
θmax = 90o
100
2]
m-80
mA [density 60
40
Current 20
0
Applied potential [V] 0 0.2 0.4 0.6 0.8 1
Exciton generarion rate [m-3s-1]
Short circuit c. d. [mA m-2]
102
100
10-2
10-4
10-6
1020 1022 1024 1026 1028 1030
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 15/22

29. Numerical results - 3
Short circuit (Vappl = 0 V)
Free charge carriers [m-3]
1019.8 1020 1020.2 1020.5 1020.8
Charge carrier
ow in both regions
) Output current
Open circuit (Vappl = 0:9 V)
Free charge carriers [m-3]
1019 1020 1021 1022 1023
Carrier con

30. nement near the interface
) Output current ' 0
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 16/22

31. Numerical results - 4
Morphology with marked tortuosity
Same interface length as in

32. ngered geometry
Current reduction of 50% due to dead-end paths
1023 Free charge carriers [m-3]
1022
1021
1020
1019
θmax = 0o
θmax = 90o
Applied potential [V]
Current density [mA m-2]
50
40
30
20
10
0
0 0.2 0.4 0.6 0.8 1
[de Falco, Porro, Sacco and Verri, CMAME (2012)]
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 17/22

33. Light harvesting capacitor - 1
Charge transport is a major issue
in organic photovoltaics.
Idea: Do not extract current and
use transient photopotentials and
displacement currents to generate
power.
h
Δ
i
+ + + + + + + + + + + +
-
+
-
+
-
+
- - -
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
+ + +
- - - - - - - - - - - -
Photoactivated capacitor: same structure as a solar cell with
dielectric layers between donor/acceptor and electrodes
Works with intermittent light
Interface dipoles/free carriers generate a photopotential
Displacement current
ows in the external circuit both with light
on and o
Stacking multiple layers absorbing dierent colors
[Garbugli, Porro al., Nano Scale (2012)]
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 18/22

34. Light harvesting capacitor - 2
Device structure similar
to that of a solar cell
=) Adapt the model
Null
ux boundary conditions
Interface potential jump due to charge-transfer states
[[']] = q
d
P on
Coupling with Kirchho's law for the external circuit
Current [nA]
400
300
200
100
0
-100
0 20 40 60 80 100
Time [ s]
Light
Experimental data
Simulation
Numerical results

35. t
the dierence in the
characteristic times of
charge and discharge
processes
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 19/22

36. Conclusions and future work
Conclusions
Development of a multiscale PDE/ODE model for organic devices
Validation on numerical results from literature and real devices
Future work
Implementation of a 3D version of the model
Coupling with an optical model
Further validation on experimental data
More accurate models for physical parameters and include traps
Application to polymer-electrolyte cells and arti

37. cial retina
prototype
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 20/22

38. Arti

39. cial Retina Model
Operating principles
Light is absorbed and
free charge carriers are
generated
Electrons pile up at the
interface and determine
capacitive and faradaic
eects
Ions rearrange in the
electrolyte
The membrane senses
the changes, polarizes
and spikes an action
potential
Neuron
Electrolyte
Active layer
ITO
OH
OH
Cl Cl
Na+ H Na+ +
H+ H+
+ + + + +
hν
Sketch of the model
Solar cell model
Poisson-Nernst-Planck model
Hodgkin{Huxley membrane
model
Butler-Volmer kinetics
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 21/22

40. Acknowledgements
Politecnico di Milano
Prof. Riccardo Sacco
Prof. Maurizio Verri
Dr. Carlo de Falco
Center for Nano Science and Technology
Prof. Guglielmo Lanzani
Dr. Maria Rosa Antognazza
Matteo Porro - Multiscale Modeling of Heterojunction Organic Photovoltaic Devices 22/22