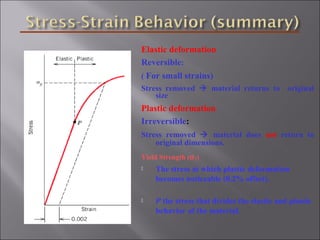
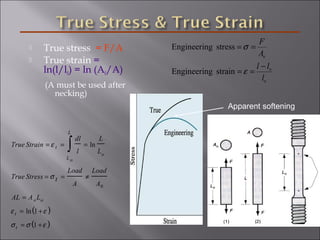
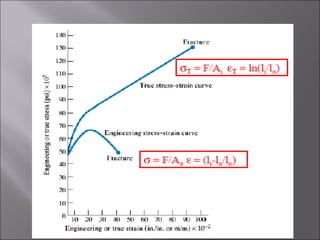
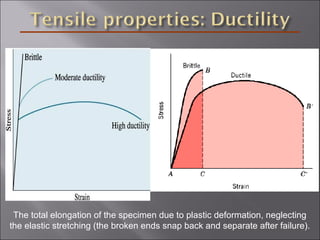
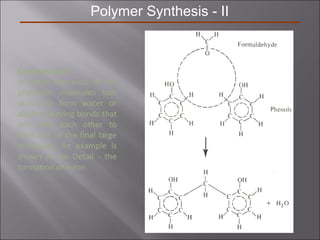
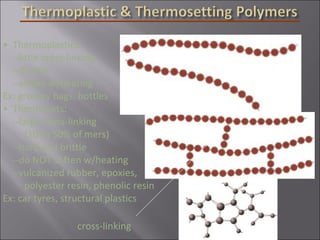
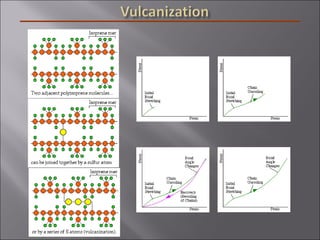
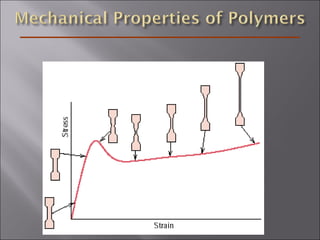
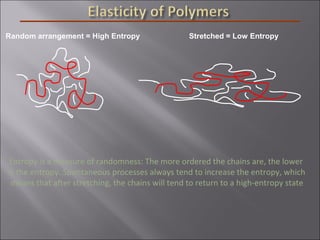
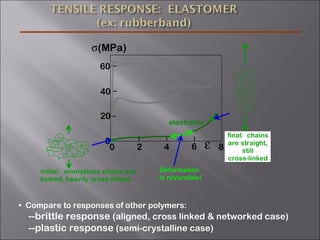
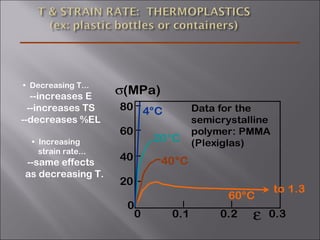
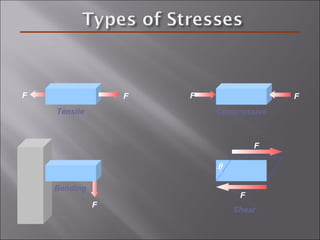
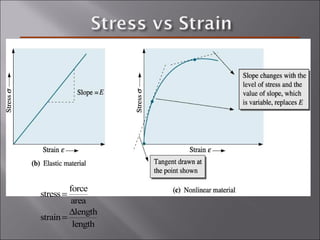
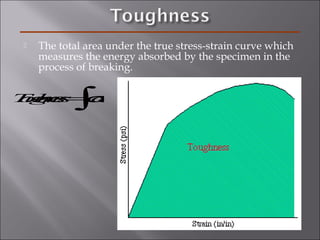
- Stress and strain are size-independent measures of load and displacement, respectively. Elastic behavior shows a linear stress-strain relation. Plastic behavior occurs when tensile stress reaches the yield strength (σy). - The elastic modulus (E or G) and yield strength characterize mechanical properties. Materials with larger E resist deformation better. Toughness is the energy to break a material. 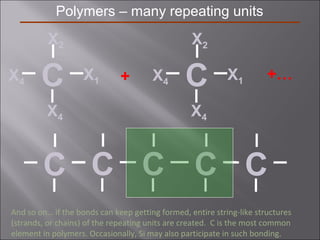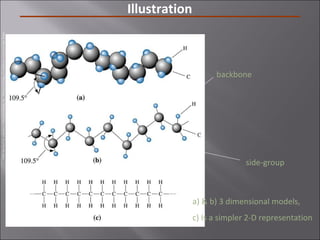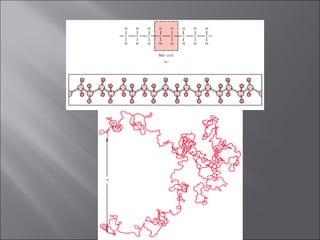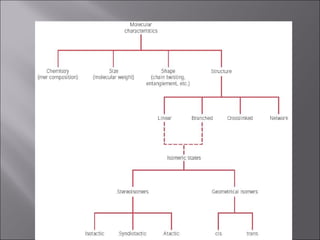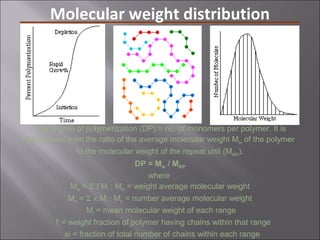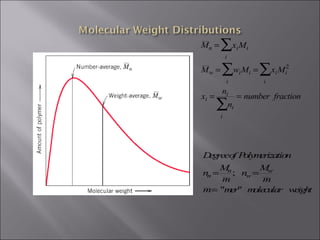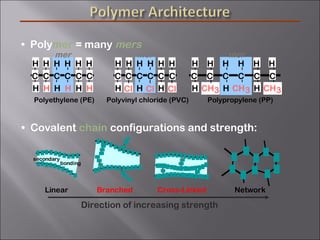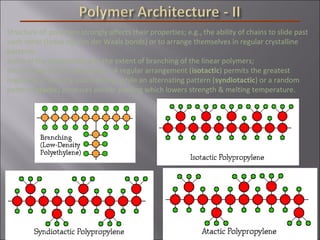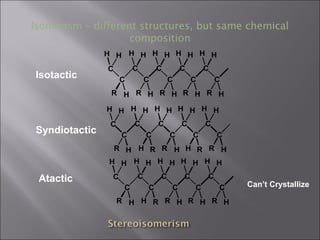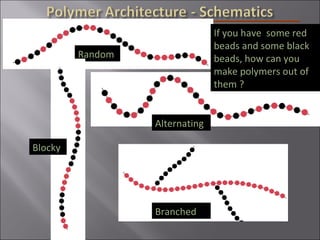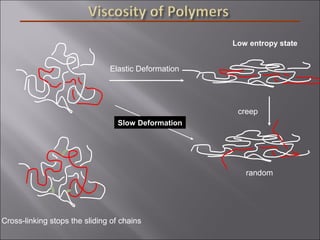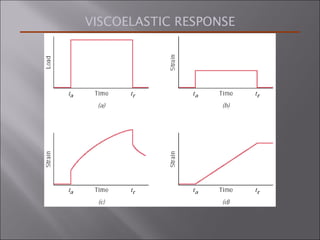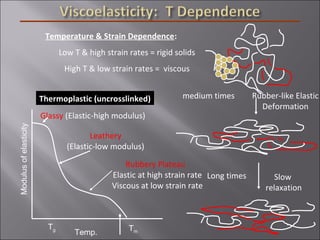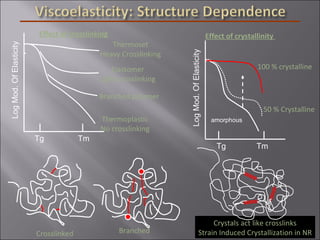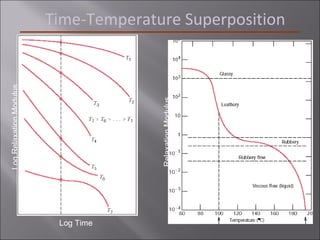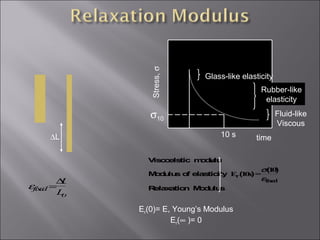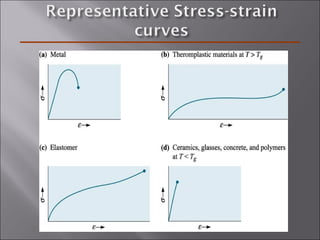- Polymers have unique time- and temperature-dependent viscoelastic behavior compared to metals and ceramics. Their properties depend on bonding, structure, and chain configurations.

2. FF
Tensile
F
Bending
FF
Compressive
F
Shear
θ
F

3. stress=
force
area
strain=
∆length
length

5.  The slope of the stress-strain
curve in the elastic region.
 Hooke’s law: E = σ/ε
 A measure of the stiffness of
the material.
 Larger the value of E, the
more resistant a material is to
deformation.
 Note: ET = Eo – bTe-To/T
where Eo and b are empirical
constants, T and To are
temperatures
Units:
E: [GPa] or [psi]
ε : dimensionless

6. Elastic deformation
Reversible:
( For small strains)
Stress removed  material returns to original
size
Plastic deformation
Irreversible:
Stress removed  material does not return to
original dimensions.
Yield Strength (σy)
 The stress at which plastic deformation
becomes noticeable (0.2% offset).
 P the stress that divides the elastic and plastic
behavior of the material.

7.  True stress = F/A
 True strain =
ln(l/l0) = ln (A0/A)
(A must be used after
necking)
0
0
0
straingEngineerin
stressgEngineerin
l
ll
A
F
−
==
==
ε
σ
Apparent softening
True Strain = ε t =
dl
l
L o
L
∫ = ln
L
Lo
True Stress = σ t =
Load
A
≠
Load
A0
AL = AoLo
εt = ln 1 +ε( )
σt = σ 1 +ε( )

9.  The total area under the true stress-strain curve which
measures the energy absorbed by the specimen in the
process of breaking.
Toughness=σdε∫

10. The total elongation of the specimen due to plastic deformation, neglecting
the elastic stretching (the broken ends snap back and separate after failure).

11. Essentials of Materials Science & Engineering
Second Edition
Authors: Donald R. Askeland & Pradeep P. Fulay
Materials Science and Engineering: An Introduction
Sixth Edition, Author: William D. Callister, Jr.
The Science and Engineering of Materials
Fourth Edition, Authors: Askeland and Phule (Fulay ?)
Introduction to Materials Science for Engineers
Sixth Edition, Author: James F. Shackelford

12. • Stress and strain: These are size-independent
measures of load and displacement, respectively.
• Elastic behavior: This reversible behavior often
shows a linear relation between stress and strain.
To minimize deformation, select a material with a
large elastic modulus (E or G).
• Plastic behavior: This permanent deformation
behavior occurs when the tensile (or compressive)
uniaxial stress reaches σy.
• Toughness: The energy needed to break a unit
volume of material.
• Ductility: The plastic strain at failure.
Note: materials selection is critically related to
mechanical behavior for design applications.

13. Polymers have unique mechanical properties vs. metals & ceramics.
Why?
Bonding, structure, configurations
Polymers and inorganic glasses exhibit viscoelastic behavior
(time and temperature dependant behavior)
Polymers may act as an elastic solid or a viscous liquid
i.e. Silly Putty (silicon rubber)
- bounces, stretches, will flatten over long times
Low Strain Rate
High extension - failure
resilient rubber ball
Elastic behavior rapid deformation
Very low Strain rate - Flatten
Flow like a viscous fluid

14. Polymers
Polymer : Materials are made up of many (poly) identical chemical units
(mers) that are joined together to construct giant molecules.
Plastics - deformable, composed of polymers plus additives. E.g. a variety
of films, coatings, fibers, adhesives, and foams. Most are distinguished by
their chemical form and composition.
The properties of polymers is related to their structures, which in turn,
depend upon the chemical composition. Many of these molecules contain
backbones of carbon atoms, they are usually called "organic" molecules
and the chemistry of their formation is taught as organic chemistry.
The most common types of polymers are lightweight, disposable, materials
for use at low temperatures. Many of these are recyclable. But polymers are
also used in textile fibers, non-stick or chemically resistant coatings,
adhesive fastenings, bulletproof windows and vests, and so on.

15. Polymers
Polymer : Materials are made up of many (poly) identical chemical
units (mers) that are joined together to construct giant molecules.
Carbon – 1s2
2s2
2p2
It has four electrons in its outermost shell, and needs four more to make a
complete stable orbital. It does this by forming covalent bonds, up to 4 of which
can be formed.
The bonds can be either single bonds, ie one electron donated by each
participating element, or double bonds (2 e-
from each), or triple bonds (3 from
each)
C X1
X2
X4
X4
Xi can be any entity ex H, O, another C, or even a similar monomer
C X1
X2
X4
X4

16. Polymers – many repeating units
C X1
X2
X4
X4 + C X1
X2
X4
X4
+…
CCCC C
And so on… if the bonds can keep getting formed, entire string-like structures
(strands, or chains) of the repeating units are created. C is the most common
element in polymers. Occasionally, Si may also participate in such bonding.

17. Classes of Polymers
Thermoplastics:
Consist of flexible linear molecular chains that are
tangled together like a plate of spaghetti or bucket
of worms. They soften when heated.
Thermosets:
Remain rigid when heated & usually consist of a
highly cross-linked, 3D network.
Elastomers:
Consist of linear polymer chains that are lightly
cross-linked. Stretching an elastomer causes chains
to partially untangle but not deform permanently
(like the thermoplastics).
Of all the materials, polymers are perhaps the most versatile, not only because the
properties can be drastically modified by simple chemistry, but the behavior is also
dependent on the architecture of the chains themselves.
From proteins to bullet-proof jackets to bottles, polymers are INDISPENSIBLE to life
as we know it

18. Illustration
©2003Brooks/Cole,adivisionofThomsonLearning,Inc.ThomsonLearning™isatrademarkusedhereinunderlicense.
a) & b) 3 dimensional models,
c) Is a simpler 2-D representation
backbone
side-group

20. Polymer Synthesis - I
Addition
in which one “mer” is added to
the structure at a time.
This process is begun by an
initiator that "opens up" a C=C
double bond, attaches itself to
one of the resulting single
bonds, & leaves the second
one dangling to repeat the
process

21. Polymer Synthesis - II
Condensation
in which the ends of the
precursor molecules lose
atoms to form water or
alcohol, leaving bonds that
join with each other to
form bits of the final large
molecules. An example is
shown in the Detail - the
formation of nylon.

23. Molecular weight distribution
The degree of polymerization (DP) = no. of monomers per polymer. It is
determined from the ratio of the average molecular weight Mw of the polymer
to the molecular weight of the repeat unit (MRP
).
DP = Mw / MRP
where
Mw = Σ fi Mi : Mw = weight average molecular weight
Mn = Σ xi Mi : Mn = number average molecular weight
Mi = mean molecular weight of each range
fi = weight fraction of polymer having chains within that range
xi = fraction of total number of chains within each range

24. Mn = xiMi
i
∑
Mw = wiMi
i
∑ = xiMi
2
i
∑
xi =
ni
ni
i
∑
= number fraction
Degreeof Polymerization
nn =
Mn
m
; nw =
Mw
m
m= "mer" molecular weight

25. Degree of polymerization (DP)- number of monomers per polymer chain, ie no. of
repeat units.
Obviously, the weight (either in AMU, or in g/mol) is the same for each repeat
unit. Then, the total weight of the polymer chain, ie its molecular weight is :-
mol. Wt. = N.Mm
where N is the number of monomers in that chain, ie the DP;
Mm is the weight of the monomer.
In a polymer sample synthesized from monomers by either condensation or
addition polymerization, one always has a distribution of DPs amongst the
resulting chains.
So let us consider that we have 100 monomers. Let the weight of each monomer
be 1g/mol (in reality, this is Hydrogen !) Let us see some ways in which we can
arrange this:
1)1 chain of N=100, ie mol. Wt. = 100
2)2 chains of N=50 each, ie mol. Wt. = 50
3)10 chains of N=10 each, ie mol. Wt. = 10
4)3 chains, 2 of N=25, and 1 of N=50

26. 3 chains, 2 of N=25, and 1 of N=50.
Now, to calculate the average molecular weight, we have two methods:
1) Take the simple numerical average, ie
(25+25+50)/3.0 = (2x25 + 1x50)/3.0 = 33.33. This value is according to the
number fraction of each type of chain (1/3 of the chains are of N=50, and 2/3
have N = 25)
2) Take the average according to the weight fraction of each chain. What is the
total weight ?
Mtotal=100
Wfraction
50
= 50/100, ie ½ , Wfraction
25
=2*25/100 = 1/2
So, taking weight fractions, we get the average molecular weight as
Mw = 50*1/2 + 25*1/2 = 25+12.5 = 37.5
So, numerical fractions, and weight fractions for mol. Wt. give different answers!
Mn = SUM(niMi)/Sum(ni) , where ni = no. of chains of length Mi
Mw = SUM(wiMi), where wi = weight fraction of chains of length Mi.
But, wi = niMi/SUM(niMi) ie the weight of that polymer (i), divided by total
weight.
50 25 25

27. Suppose we want to find out the average population of each state.*
We can go to each senator of each state and find out what the population of
their state is, and then divide that number by 100.
This number is the number-average population for each state. This is exactly
similar to the Mn that we calculated earlier, ie no. av. Mol. wt.. Problem ?
Yes, of course. What do we do about say, CA and AK ?
Now, senators are busy, so we ask congressmen from each state. Then, we take
the value that each congressman/congresswoman gives us, and then divide
by the number of congresscritters. What value do we get ? Certainly one
different from our earlier attempt ! Problem ?
Now the value is much higher than before. This is exactly similar to the Mw that
we calculated earlier, ie to weight av. mol. Wt.
Is this value MUCH more representative (eh eh !) of the average population of
each state ? Well, not really. But at least, it is an average.
We learn about these differences, because different measurement techniques
measure different averages, and the ratio of Mw to Mn, called the Poly
Dispersity Index (PDI) often determines properties.
* taken from “Polymer Physics” by M. Rubinstein & R. H. Colby, 1st
edition, OUP

28. • Polymer = many mers
• Covalent chain configurations and strength:
Direction of increasing strength
Branched Cross-Linked NetworkLinear
secondary
bonding
C C C C C C
HHHHHH
HHHHHH
Polyethylene (PE)
mer
ClCl Cl
C C C C C C
HHH
HHHHHH
Polyvinyl chloride (PVC)
mer
Polypropylene (PP)
CH3
C C C C C C
HHH
HHHHHH
CH3 CH3
mer

29. Structure of polymers strongly affects their properties; e.g., the ability of chains to slide past
each other (breaking Van der Waals bonds) or to arrange themselves in regular crystalline
patterns.
Some of the parameters are: the extent of branching of the linear polymers;
the arrangement of side groups. A regular arrangement (isotactic) permits the greatest
regularity of packing and bonding, while an alternating pattern (syndiotactic) or a random
pattern (atactic) produces poorer packing which lowers strength & melting temperature.

30. C
C
HH
R H
C
C
HH
R H
C
C
HH
R H
C
C
HH
R H
C
C
HH
R H
C
C
HH
R H
C
C
HH
H R
C
C
HH
R H
C
C
HH
H R
C
C
HH
R H
C
C
HH
R H
C
C
HH
H R
C
C
HH
R H
C
C
HH
R H
C
C
HH
R H
Isotactic
Syndiotactic
Atactic
Can’t Crystallize
Isomerism – different structures, but same chemical
composition

31. Random
Alternating
Branched
If you have some red
beads and some black
beads, how can you
make polymers out of
them ?
Blocky

32. We have discussed polymers comprised of a single kind of a monomer,
ie just one repeating entity. However, this is not unique: we can
synthesize polymers that consist of different repeating units, and such
polymers are called copolymers
The combination of different mers allows flexibility in selecting
properties, but the way in which the mers are combined is also
important. Two different mers can be alternating, random, or in blocks
along the backbone or grafted on as branches.

33. • Thermoplastics:
--little cross-linking
--ductile
--soften w/heating
Ex: grocery bags, bottles
• Thermosets:
--large cross-linking
(10 to 50% of mers)
--hard and brittle
--do NOT soften w/heating
--vulcanized rubber, epoxies,
polyester resin, phenolic resin
Ex: car tyres, structural plastics
cross-linking

34. In thermoset, the network is inter-connnected in a non-regular fashion. Elastomers
belong to the first category. Polyisoprene, the hydrocarbon that constitutes raw natural
rubber, is an example. It contains unsaturated C=C bonds, and when vulcanizing
rubber, sulfur is added to promote crosslinks. Two S atoms are required to fully saturate
a pair of –C=C— bonds and link a pair of adjacent molecules (mers) as indicated in the
reaction.
Without vulcanization, rubber is soft and sticky and flows viscously even at room
temperature. By crosslinking about 10% of the sites, the rubber attains mechanical
stability while preserving its flexibility. Hard rubber materials contain even greater sulfur
additions.

36. • Molecular weight Mw: Mass of a mole of chains.
• Tensile strength (TS):
--often increases with Mw.
--Why? Longer chains are entangled (anchored) better.
• % Crystallinity: % of material that is crystalline.
--TS and E often increase
with % crystallinity.
--Annealing causes
crystalline regions
to grow. % crystallinity
increases.
crystalline
region
amorphous
region
smaller Mw larger Mw
Molecular weight, Crystallinity
and Properties

37. ~10 nm spacing
Oriented chains with long-range order
Amorphous disordered polymer chains in
the “intercrystalline” region

39. Random arrangement = High Entropy Stretched = Low Entropy
Entropy is a measure of randomness: The more ordered the chains are, the lower
is the entropy. Spontaneous processes always tend to increase the entropy, which
means that after stretching, the chains will tend to return to a high-entropy state

40. Elastic Deformation
creep
Cross-linking stops the sliding of chains
random
Slow Deformation
Low entropy state

41. Elastic
ViscousViscoelastic
VISCOELASTIC RESPONSE

42. Temperature & Strain Dependence:
Low T & high strain rates = rigid solids
High T & low strain rates = viscous
Rubber-like Elastic
Deformation
Slow
relaxation
Glassy (Elastic-high modulus)
Leathery
(Elastic-low modulus)
Thermoplastic (uncrosslinked)
Tg Tm
Modulusofelasticity
Temp.
Rubbery Plateau
Elastic at high strain rate
Viscous at low strain rate
medium times
Long times

43. Crosslinked Branched
Effect of crosslinking
Thermoset
Heavy Crosslinking
Elastomer
Light crosslinking
Effect of crystallinity
Tg Tm
LogMod.OfElasticity
amorphous
50 % Crystalline
100 % crystalline
Tm
LogMod.OfElasticity
Thermoplastic
No crosslinking
Tg
Branched polymer
Crystals act like crosslinks
Strain Induced Crystallization in NR

44. • Compare to responses of other polymers:
--brittle response (aligned, cross linked & networked case)
--plastic response (semi-crystalline case)
initial: amorphous chains are
kinked, heavily cross-linked.
final: chains
are straight,
still
cross-linked
0
20
40
60
0 2 4 6
σ(MPa)
ε 8
x
x
x
elastomer
plastic failure
brittle failure
Deformation
is reversible!

45. • Decreasing T...
--increases E
--increases TS
--decreases %EL
• Increasing
strain rate...
--same effects
as decreasing T.
20
40
60
80
0
0 0.1 0.2 0.3
4°C
20°C
40°C
60°C
to 1.3
σ(MPa)
ε
Data for the
semicrystalline
polymer: PMMA
(Plexiglas)

46. • Stress relaxation test:
Er (t) =
σ(t)
εo
--strain to εο and hold.
--observe decrease in
stress with time.
• Relaxation modulus:
• Data: Large drop in Er
for T > Tg.
(amorphous
polystyrene)
103
101
10-1
10-3
105
60 100 140 180
rigid solid
(small relax)
viscous liquid
(large relax)
transition
region
T(°C)
Tg
Er(10s)
in MPa
time
strain
tensile test
εo
tσ( )

47. Time-Temperature Superposition
Log Time
LogRelaxationModulus
RelaxationModulus
Hi T
Lo T

48. time
Stress,σ
10 s
σ10
∆L
εfixed =
∆L
Lo
Er(0)= E, Young’s Modulus
Er(∞ )= 0
Glass-like elasticity
Rubber-like
elasticity
Fluid-like
Viscous
Viscoelstic modulus
Modulus of elasticity Er(10s)=
σ(10)
εfixed
Relaxation Modulus