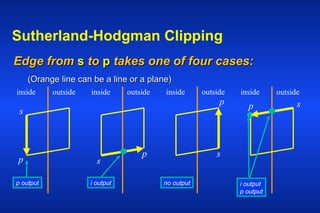
Clipping polygons is more complex than clipping lines because it involves considering the polygon as a whole rather than just its individual line segments. The Sutherland-Hodgman algorithm clips polygons by considering each edge of the clipping region individually and clipping the subject polygon against that edge, resulting in a new clipped polygon. This process is repeated for each clipping region edge until the polygon is fully clipped. The algorithm takes as input a list of polygon vertices and outputs a new list of clipped polygon vertices.