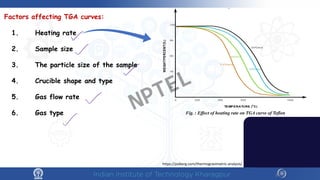
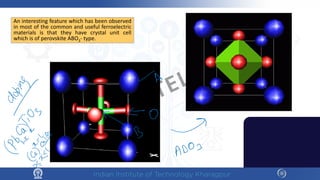
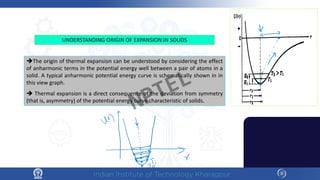
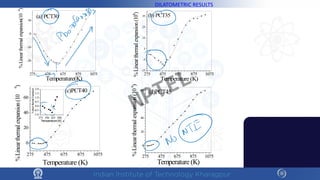
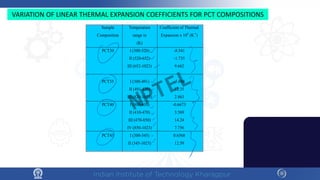
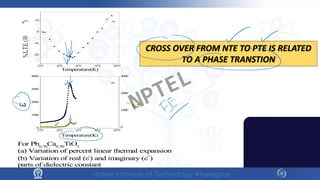
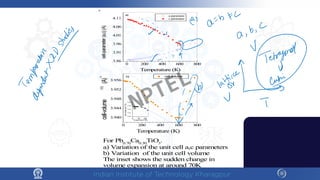
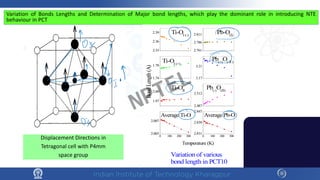
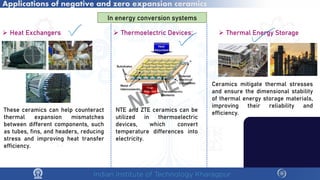
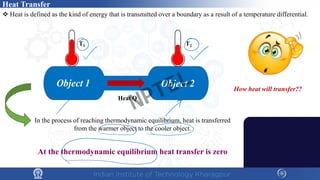
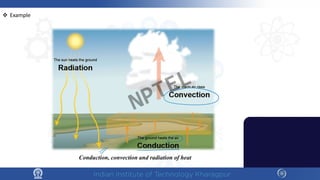
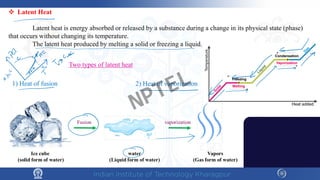
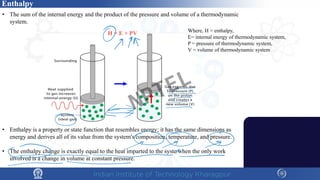
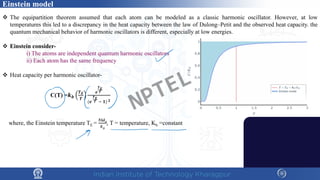
The document discusses the thermal properties of solids, focusing on heat capacity, thermal expansion, thermal stress, and thermal conductivity. It explains how materials respond to temperature changes and highlights key concepts like specific heat, coefficients of expansion, and the behavior of ceramics, including negative and zero thermal expansion. Additionally, it covers the practical implications of these properties in materials science and engineering.


























































![4
Introduction
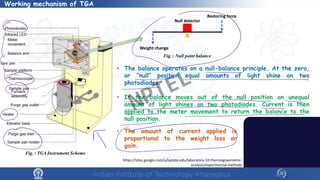
Thermal Gravimetric Analysis
Temperature
variation
Mass change Microbalance
causing detected by
• Thermogravimetry or thermogravimetric analysis is an analytical
method that records the mass change by temperature of a
sample that is facing a controlled temperature profile.
• The sample undergo heating, cooling or isothermal steps.
• The resulting measurement signal gives the absolute mass
change in [mg] and relative mass change in [%].
What is thermogravimetric analysis?
Fig. : TGA Sensor setup in a typical
thermogravimetric analyzer
NPTEL](https://image.slidesharecdn.com/lm-week6-240831073949-e89cd259/85/PHYSICS-MATERIAL-FUNCTION-PROPERTY-DEVICES-pdf-72-320.jpg)