The document summarizes an experiment that investigated how the mass of a ball affects the area of the impact crater formed when dropped from a fixed height onto sand. Six ping pong balls of varying masses were each dropped from 79.3cm above sand and the diameter of the resulting craters were measured. The results showed a quadratic relationship between ball mass and crater area, with area approaching the ball diameter as mass decreased. The mass and crater area were found to be related by the equation: Area = 0.0105m2 + 0.105m, where m is the mass in kilograms. Some improvements to the experiment are identified, such as ensuring the added mass inside the balls can move freely.

1. Emmanuel Castaño
Physics HL1
Period 1; Mr. Eales
Introduction:
When a depression is made from a high velocity impact on a surface, it is called in impact
crater. When an object is in an inelastic collision, such as when a steel ball hits clay, the kinetic
energy from the source is not conserved after the collision. However if an inelastic collision
takes place somewhere other than a vacuum, there are other factors, such as friction, that can
cause some of that kinetic energy to be lost by being converted into other types of energy such as
sound or thermal energy before the collision happens. In this experiment, six differently massed
ping pong balls were dropped from a fixed height onto a flattened surface of sand and the area of
the mouth of the craters made was measured. The formula for kinetic energy is:
[EQ 1]
Where , is mass, and is velocity. If a ball is dropped from a fixed height, the only
factor that changes the kinetic energy transferred on impact is the mass of the ball that is
dropped.
The radius of the mouth of each circular crater was measured, and the equation:
[EQ 2]
Was used to find the area the impact crater formed after each trial. In this experiment, the
question being researched is, how does the mass of a ball affect the area of the mouth of the
impact crater made in the sand when dropped from a fixed height.
It is predicted that since the height of the drop remains constant, the area of the craters
formed by the balls will exhibit quadratic growth to the increase of the mass of the balls, if, for
the purpose of the experiment, the smallest the diameter of the crater can be is the diameter of
the ball. A proportional relationship is predicted between the mass of the balls and the diameter
of the crater since as an object’s mass decreases, so does its kinetic energy if it’s velocity is kept
constant. As the kinetic energy approaches zero, the object should throw as little sand as possible
on impact, and therefore the crater’s diameter should approach the diameter of the ball. Since

2. area is found by using the formula, , if there is a proportional relationship between the
mass of the balls and the diameter of the crater, and since the radius is half of the diameter, the
relationship between the mass of the balls and the area of the crater should be exponential, with
the y-axis being near 0.00108m2 (or half of the diameter of the ball, squared, multiplied by Pi).
Design:
Research Question:
How does the mass of a ball affect the area of the mouth of the impact crater made in the
sand when dropped from a fixed height?
Variables:
In this experiment, the independent variable is the mass of the balls being dropped, and
the dependent variable is the area of the mouth of the crater that is made after the ball has hit the
sand. Identical ping pong balls filled with lead shot and glue were used to make six different ping
pong balls different masses. A scale was used to measure the mass of the balls to an accuracy of
0.00001kg. The diameter of the crater made by the balls on each trail was measured using a
vernier caliper to accurately measure it to an accuracy of 0.001m. Only trials that had the same
diameter ± 0.5mm in at least three different directions were used to ensure that if the ball had any
spin while falling, it did not affect the diameter of the crater in any one direction.
There were also other variables that were kept constant to obtain results with higher
levels of reliability. The same scale was used to mass each of the six ping pong balls to avoid any
possible uncertainty of using different scales. Also, the six ping pong balls were of the same
kind, with a 3.7cm ± 0.1cm diameter; this ensures that the size of the ping pong balls is not a
factor changing the size of the crater made. Another controlled variable was the height the ball
was dropped from. To keep the velocity of the balls the same when hitting the sand, they were
dropped from a height of 79.3cm ± 0.1cm above the point of impact. Lastly, before each trial, the
sand was loosened and then flattened by using the same method during all of the trials to ensure
that the sand as equally compact during each trial as possible, therefore having a minimal effect
in each of the trial’s crater size.

3. Massed ping pong ball
79.3cm
Plastic Basin
Sand Roll of tape
Figure 1: shows a diagram and picture of the experimental set up for this lab.
Procedure:
To set up this experiment, a large plastic basin was filled with sand and placed on the
floor beside a table. An object, in this case, a roll of 4.8cm thick tape, was placed at the bottom
of the basin and before each trial, after the sand was loosened, a ruler was placed on top of the
roll of tape and turned around the basin to flatten a portion of the sand. Once the sand was ready,
one of six differently massed ping pong balls was dropped, not rolled, from the fixed height (in
this case it was the table) onto the sand. The balls were carefully removed from the sand and a
vernier caliper was used to measure the crater made by the ball in three different directions to
ensure that the spin off the ball did not increase the crater on the ball in any direction. If this was
the case, two more trials were taken with that ping pong ball and then the procedure was repeated
with the other five differently massed balls.

4. Data Collection and Processing:
Mass Diameter of Crater Average
(kg) (m) (m)
Ball
(± 0.0005)
(± 0.00001) (± 0.002)
Trial 1 Trial 2 Trial 3
1 0.00687 0.042 0.043 0.044 0.043
2 0.02738 0.050 0.052 0.051 0.051
3 0.04679 0.061 0.059 0.063 0.061
4 0.08942 0.082 0.082 0.082 0.082
5 0.09975 0.086 0.087 0.085 0.086
6 0.12799 0.097 0.098 0.096 0.097
Table 1: shows diameters of a crater differently massed
balls have made after being dropped on sand from a fixed
height.
Average Diameter of Crater Radius Area (πr2)
Ball (m) (m) (m2)
(± 0.002) (± 0.001) (± 0.00003)
1 0.043 0.0213 0.00143
2 0.051 0.0255 0.00204
3 0.061 0.0340 0.00295
4 0.082 0.0410 0.00528
5 0.086 0.0430 0.00581
6 0.097 0.0485 0.00739
Table 2: shows how the diameters of the craters are used to
find the top area of the crater made by the different balls.

5. Figure 2: shows the relationship between the ball’s mass and the area of the
mouth of the impact crater it formed when dropped from a fixed height.
Figure 3: shows the maximum and minimum relationship between the ball’s mass and
the area of the mouth of the impact crater it formed when dropped from a fixed height.

6. Sample Calculations:
Average Diameter of Crater Uncertainty (See Table 1):
0.063m - 0.059m = 0.004m  0.004m / 2 = 0.002m
Average Radius of Crater Uncertainty (See Table 2):
0.063m / 2 = 0.0315m
0.059m / 2 = 0.0295m
0.0315m – 0.0295m = 0.002m  0.002m / 2 = 0.001m
Area Uncertainty (See Table 2):
π0.4862 = 0.00742
π0.4842 = 0.00736
0.00742m2 – 0.00736 m2 = 0.00006 m2  0.00006m2 / 2 = 0.00003m2
Uncertainty for variable A:
0.105m2/kg – 0.080m2/kg = 0.025m2/kg  0.025m2/kg / 2 = 0.0125m2/kg
Uncertainty for variable C:
0.00130m2- 0.00107m2 = 0.00027m2  0.00027m2 / 2 = 0.000135m2
Conclusion:
The results in Figure 2 show that there is a quadratic relationship between the mass of the
balls dropped on the sand, and the area of the mouth of the crater formed. Since the mass of the
ball increase, so did the kinetic energy of the ball, and as that increased, so the area of the mouth
of the crater. Figure 2 shows that the graph goes through the y-axis at 0.001076m2. This rounds
up to 0.00108m2 which is actually the area of the center of the balls that were used in this
experiment. This, quite accurately, shows that as the mass of a ball decreases, the area of the
crater approaches the center area of the ball.

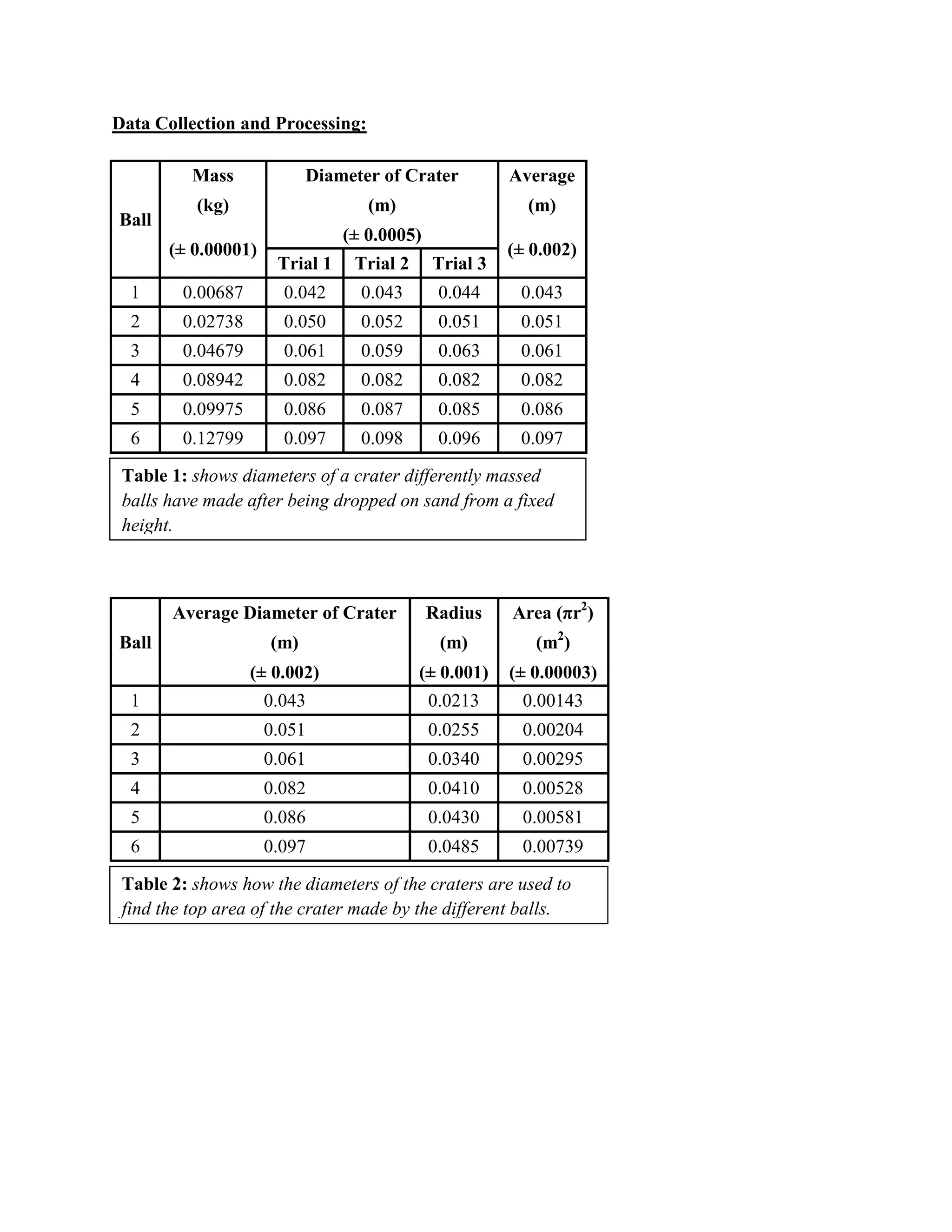
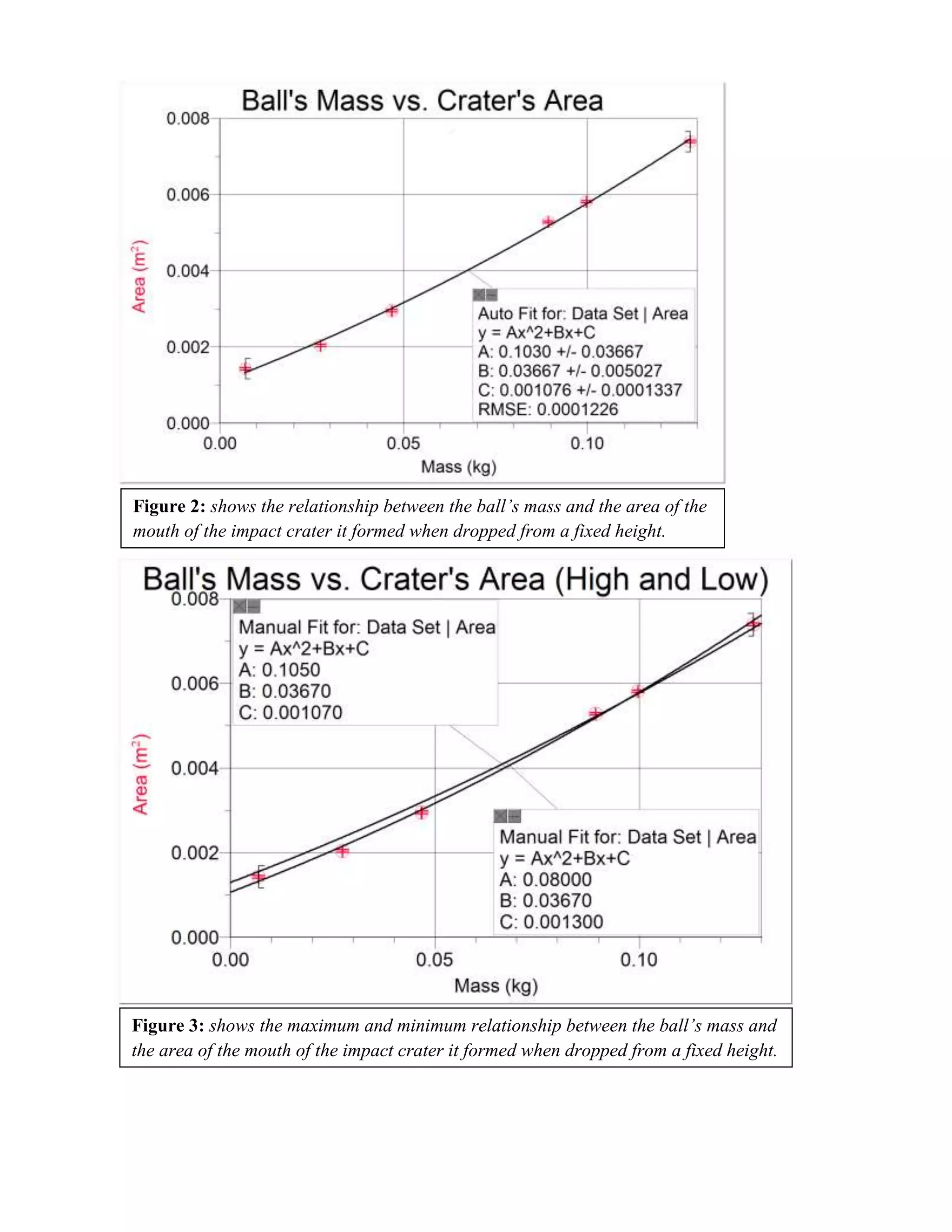
7. The equation to Figure 3 shows that from the data collected:
[EQ 3]
Where is the area of the mouth of the crater in meters squared, and is the mass of the
ball in kilograms. Even though Equation 3 is only applicable to a situation where the balls used
have a diameter of 3.7cm ± 0.1cm, are dropped from a height of 79.3cm ± 0.1cm above the point
of impact, and are dropped onto sand of the compactness used in this experiment, the
relationship between the mass of the balls dropped and the area of the crater should be
consistent. Since the change in mass directly affects the kinetic energy of the ball before impact,
this correlation is justifiable, and since to find the area half of the diameter squared is used,
multiplied by the constant Pi, the quadratic relationship between mass and area can be applied to
many other situations, such as the area affected by the splash after different massed basketballs
are dropped into water.
Evaluation:
Overall, even though there were many controlled variables in this experiment, a few were
not foreseen, such as, the lead shot and glue used to increase the mass of the ping pong balls not
moving freely inside the ball, and the potential altering of the result when removing the ball from
the sand before measuring the diameter of the crater. Some of the ping pongs used in this
experiment had lead shot and glue inside of them that moved freely so that on impact, it was at
the bottom of the ball. However, on some of the balls, the mass inside did not move, perhaps due
to it melting onto the side of the ball, and therefore, on impact, unless that side of the ball hit the
sand, it could have affected the results. To avoid this issue, before beginning this experiment,
each of the balls should have been filled with lead shot so that it does not melt onto the side of
the ball like glue, and the mobility of the mass inside the ball should be tested. To avoid any
altering of the results when removing the ball from the sand after impact, a larger vernier caliper
could be used to measure around the ball in order to not have its removal move any of the sand
around it.