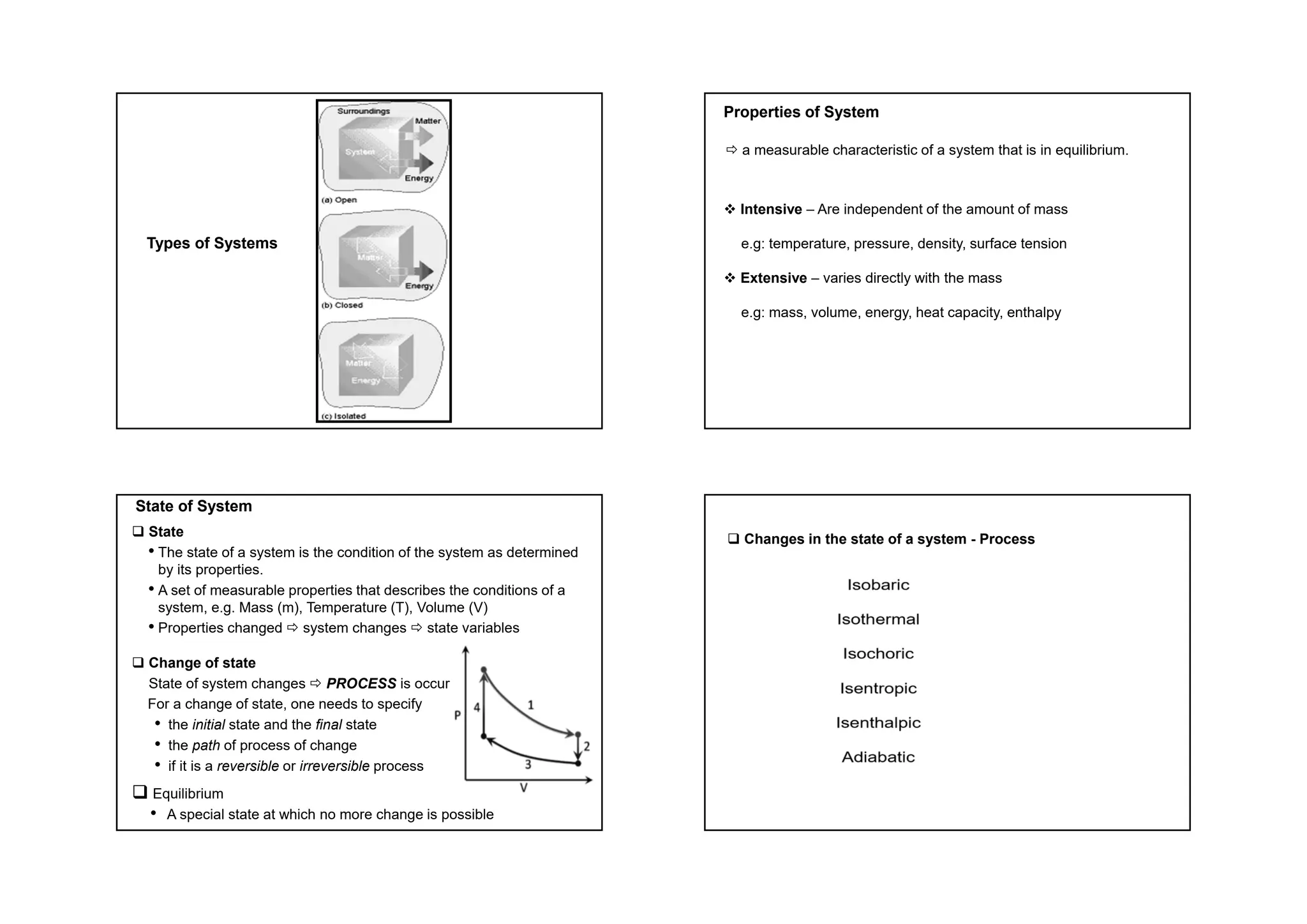
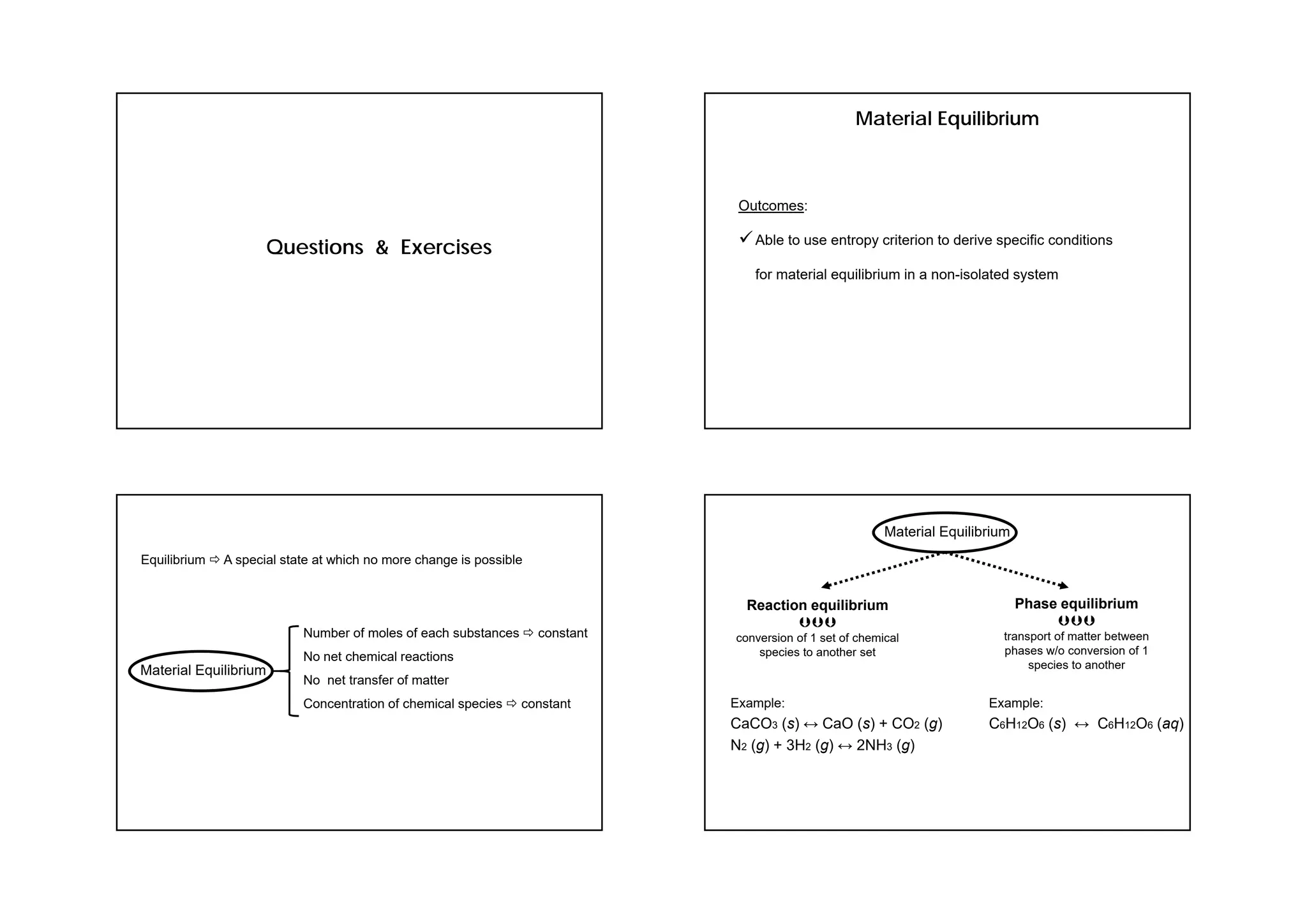
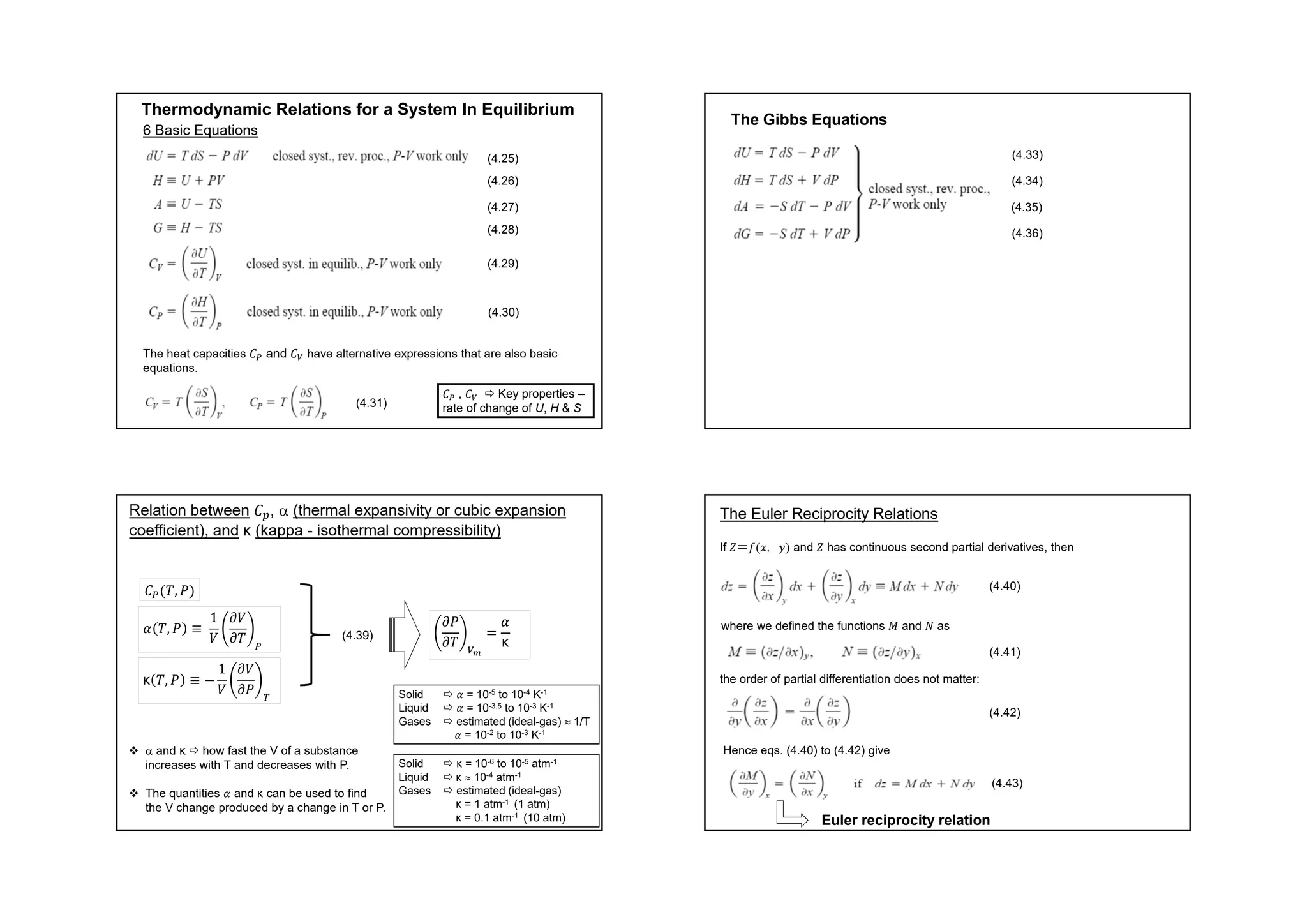
This document provides information about a physical chemistry course for the 2018/2019 semester. It includes: - Details about the course instructors and their contact information. - An outline of the course content including topics to be covered, references, objectives, outcomes and assessment details. - The course is worth 3 credit units and students will be evaluated based on exams (60%), coursework (40%) including tests, assignments and quizzes. - Class times and locations are provided, with notes that attendance is mandatory or students may be prevented from sitting exams.

1. School of Chemical Engineering
EKC 113/3
Physical Chemistry
( Kimia Fizikal )
Sem. I - 2018/2019
DR. IRVAN DAHLAN
(chirvan@usm.my)
PROF. DR. MOHD ROSLEE OTHMAN
(chroslee@usm.my)
E - learning
https://elearning.usm.my/sidang1819/
 Note
 Questions of exercise, assignment, etc.
 Other info
 Feedback/Reflection
COURSE OUTLINE
 Course – Physical Chemistry (EKC 113)
 Credit Unit – 3 Unit
 Evaluation:
Exam – 60%
Course Work – 40 %
CW Assessment/Evaluation
- Test (15%)
- Assignment (20%)
- Quiz (5%)
Class/Tutorial:
Monday (08.00-09.00) – DK5
(16.00-17.00) – DK5
Friday (15.00-17.00) - DK5
IMPORTANT NOTES:
The presence of students to
the lecture/tutorial class is
mandatory. If absent without
reason, the student may be
prevented from sitting for the
TEST / FINAL EXAMINATION.
COURSE OBJECTIVE
This course introduces the basic concept of
thermodynamics. This includes perception of concept
on heat, work, internal energy, enthalpy, entropy,
Gibb’s free energy and Helmholtz energy. The
students are also introduced to the concept of
chemical potential and equilibrium, thermo chemistry,
chemical kinetics and electrochemical system.

2. COURSE OUTCOME (CO)
1. Apply the concept of solutions, electrolytes, standard
electrode potential in an electrochemical system.
2. Analyze various problems of ideal and non-ideal fluids
in a thermodynamic system.
3. Recognize the importance of material, reaction
equilibrium and kinetics through literature review.
COURSE TOPICS
REFERENCES
Main
1. Levine IN, “Physical Chemistry”, McGraw Hill, 6th
Edition, 2009.
Additional
2. Atkins P.W., “Physical Chemistry”, 9th Edition, Oxford
Publisher, 2010.
3. Alberty R. A, Silbey R.J., “Physical Chemistry”, 4th
Edition., John Wiley, 2005
4. Othman MR, Idris I. Panduan Asas Kimia Fizik untuk
Jurutera Kimia. USM. 1st Edition, 2017.
5. Lionel M. Raff “Principle of Physical Chemistry” Prentice
Hall 1st Edition, 2001.

3.  Physical chemistry & thermodynamics
 Physical quantities
 mass, length, time, velocity, density, specific volume,
temperature, and pressure
 Unit & converting between different sets of units
Introduction & Review
Introduction & Review
 What is Physical Chemistry ?
Laws of physics Mathematical models Chemical insight/system
• It applies the principles, practices and concepts of physics
such as motion, energy, force, time, thermodynamics, quantum
chemistry, statistical chemistry and dynamic.
macroscopic
microscopic
 Pre-requisites
Thermodynamics - Review
 study of heat, work, energy, and the changes
 relationships between the macroscopic properties of a system
Universe = System + Surrounding

4. Types of Systems
Properties of System
 a measurable characteristic of a system that is in equilibrium.
 Intensive – Are independent of the amount of mass
e.g: temperature, pressure, density, surface tension
 Extensive – varies directly with the mass
e.g: mass, volume, energy, heat capacity, enthalpy
State of System
 State
• The state of a system is the condition of the system as determined
by its properties.
• A set of measurable properties that describes the conditions of a
system, e.g. Mass (m), Temperature (T), Volume (V)
• Properties changed  system changes  state variables
 Change of state
State of system changes  PROCESS is occur
For a change of state, one needs to specify
• the initial state and the final state
• the path of process of change
• if it is a reversible or irreversible process
 Equilibrium
• A special state at which no more change is possible
 Changes in the state of a system - Process

5.  Types of Thermodynamics Processes
• Cyclic process – when a system in a given initial state goes through
various processes and finally return to its initial state.
• Reversible process – it is defined as a process that, once having take
place it can be reversed.
• Irreversible process – a process that cannot return both the system and
surrounding to their original conditions
• Spontaneous process – take place by itself or initiation (e.g.
evaporation of water in open vessel, dissolution of salt in water, flow of
water down a hill, combination of oxygen and hydrogen to form water,
lighting of candle is initiated by ignition)
• Non Spontaneous Process – cannot take place by itself or initiation (e.g.
flow of heat from cold body to hot body, flow of water up the hill,
dissolution of sand in water).
Work, Heat and Energy
Work = Force x Distance
 The principal form of work involves changes
in volume of the system under a pressure
(P-V Work)
Reversible P-V Work
dw = PA dx
dw = –P dV
𝑤 𝑃 𝑑𝑉
Energy = capacity of a system to do work
• Kinetic energy energy due to motion
• Potential energy  energy due to position, or the
configuration of a system
• Internal energy  energy stored in the molecules (both
potential & kinetic) associated with T
• Chemical energy  energy due to chemical composition
• Nuclear energy  subatomic energy (i.e, energy stored in
the nucleus of an atom)

6. Heat = Transfer of thermal energy
System
q ≡ Heat
Heat into system: q > 0
Heat out of system: q < 0
q > 0 q < 0
Endothermic
Endothermic
Exothermic
Exothermic
Some Thermodynamics Quantities
Internal Energy  Every system is associated with a definite
amount of energy  internal energy (E or U)
 T, P, and chemical nature of the substance
Change in Internal Energy
 The change in internal energy in a chemical
reaction is the difference in the internal
energies of the products and the reactants
ΔE = E(products) - E(reactants)
Enthalpy (H)  (heat content of a system)  sum of the
internal energy and the product of its pressure
and volume
H = E + PV
∆𝐻 𝑞 𝐶 𝑇 𝑑𝑇 (constant P)
 It is the difference in the enthalpies of
the products and the reactants
ΔH = H(products) - H(reactants)
Change In Enthalpy
Entropy (S)  Measure of the randomness or disorder of the
system - depends on T and increases with T
 The greater the randomness, the greater S
 Entropy of a crystalline substance is minimum in
the solid state and maximum in the gaseous state
Change in entropy
 Equal to heat absorbed isothermally and
reversibly during a process divided by absolute
T at which heat is adsorbed
Δ S = qrev / T

7. Laws of Thermodynamics
Zeroth Law of Thermodynamics
If two systems are in thermal equilibrium with a third system,
there are also in thermal equilibrium with one another
1 3 2
(T1) (T3) (T2)
If T1 = T3 and T2 = T3, then T1 = T2
1st Law of Thermodynamics
 Conservation of internal E
 E can neither be created nor destroyed ( converted from one
form to other) - Quantity same
 The total E of the universe remains constant
 The change in internal E of a closed system is equal to the E
added to it (as a result of heat) PLUS the work that is done on the
system
ΔE = q + W (closed system)
ΔE = 0 (isolated system)
2nd Law of Thermodynamics
 E is transferred/transformed, more & more E is wasted - Quality 
 Use entropy (S) to identify the spontaneous changes.
 In an isolated system - S never 
 In an non isolated system the total energy of both the system and
surrounding must increase or must be positive
 The total ΔS of the universe must tend to increase in a spontaneous process
ΔS (total) = ΔS system + ΔS surrounding > 0
 All spontaneous or naturally occurring processes are irreversible
3rd Law of Thermodynamics
 Provides an absolute reference point for measuring entropy
 Comes from the way that various gases were supercooled into a
liquid form  absolute zero
 It is impossible to reach absolute zero (0 K) in any number of
finite processes - it would take infinitely many steps
𝒄𝒂𝒓𝒏𝒐𝒕 𝒄𝒚𝒄𝒍𝒆 𝟏
𝑻𝑳
𝑻𝑯
 The entropy of all perfectly crystalline solids may be taken as
zero at the absolute T

8. Questions & Exercises
Material Equilibrium
Outcomes:
Able to use entropy criterion to derive specific conditions
for material equilibrium in a non-isolated system
Equilibrium  A special state at which no more change is possible
Material Equilibrium
Number of moles of each substances  constant
No net chemical reactions
No net transfer of matter
Concentration of chemical species  constant
Material Equilibrium
Example:
C6H12O6 (s) ↔ C6H12O6 (aq)
Example:
CaCO3 (s) ↔ CaO (s) + CO2 (g)
N2 (g) + 3H2 (g) ↔ 2NH3 (g)
Reaction equilibrium

conversion of 1 set of chemical
species to another set
Phase equilibrium

transport of matter between
phases w/o conversion of 1
species to another

9. Entropy & Equilibrium
 Consider an isolated system that is not at material equilibrium
 spontaneous chemical reaction or transport of matter between phases are
irreversible processes that increase the S.
 processes continue until the S is maximized  once the S is maximized,
further processes can only decrease S, thus violate 2nd Law.
Thus, criteria for equilibrium in an isolated system is the maximization of the
system’s entropy S.
 Consider a closed system at material equilibrium
 condition for material equilibrium in the system is maximization of the total
entropy of the system plus its surroundings
(4.1)
Reaction equilibrium (studied):
1) Reaction that involve gases
e.g.: chemicals put in container of fixed
volume, and the system is allowed to
reach equilibrium at constant T and V.
2) Reaction in liquid solutions
e.g.: the system is usually held at
atmospheric P and allowed to reach
equilibrium at constant T and P.
To find equilibrium criteria
for these conditions
Fig.: A closed system that is in
mechanical and thermal equilibrium
but not in material equilibrium.
Since system and surroundings are isolated, we have
Since, the chemical reaction or matter transport within
the non equilibrium system is irreversible, dSuniv must
be positive
The surroundings are in thermodynamic
equilibrium throughout the process. Therefore,
the heat transfer is reversible, and
Fig.: A closed system that is in mechanical and
thermal equilibrium but not in material equilibrium.
The systems is not in thermodynamic equilibrium, and the process involves an
irreversible change in the system, therefore
Equation (4.2) to (4.4) gives
(4.2)
(4.3)
(4.4)
When the system has reached material equilibrium, any infinitesimal process is a
change from a system at equilibrium to one infinitesimally close to equilibrium and
hence is a reversible process.
Thus, at material equilibrium we have,
Combining Eq. (4.5) and (4.7) gives
For a reversible process 𝑑𝑆 𝑑𝑞/𝑇
For an irreversible chemical reaction or phase change
(4.5)
(4.6)
(4.7)
𝑑𝑆 𝑑𝑞/𝑇

10. From the first law for a closed system
Multiply Eq. (4.7) with T gives
Hence for a closed system in mechanical and thermal equilibrium (combining
Eq. (a) & (b), we have
(a)
(b)
(4.8)
Helmholtz and Gibbs Energies
maximum amount of work that
can be obtained from a system
(spontaneous process)
at constant V and T at constant P and T
dA = 0 at equilibrium, const. T, V dG = 0at equilibrium, const. T, P
Helmholtz Free Energy
A  U - TS
Consider material equilibrium at constant T and V
previous (4.8)
(4.9)
(4.10)
(4.11)
If the system can do only P-V work (𝑑𝑤 𝑃𝑑𝑉) then,
(4.12)
At constant T and V, we have 𝑑𝑇 𝑑𝑉 0 then (4.12) becomes
(4.13)
𝑑 𝑈 𝑇𝑆 0
(U –TS has reached a
minimum  equilibrium )
(4.14)
Gibbs Free Energy
G  H – TS  U + PV – TS
Consider material equilibrium for constant T and P
Gibbs Free Energy Combined H and S function that determines spontaneity of a process
OR the amount of E that is left after a reaction take place
previous (4.8)
(4.15)
At constant T and P, we have 𝑑𝑇 𝑑𝑃 0 then (4.15) becomes
(4.16)
(4.17)

11. Summary:
In a closed system capable of doing only P-V work, the constant-T-and-V
material equilibrium condition is the minimization of the Helmholtz energy 𝐴,
and the constant-T-and-P material-equilibrium condition is the minimization
of the Gibbs energy 𝐺
(4.18)
(4.19)
Example
Calculate G and A for the vaporization of 1 mol of H2O at
1 atm and 100°C (at this condition, the density of H2O is
0.958 g/cm3).
Questions & Exercises
Exercise
Consider the metabolism of 1 mol glucose to water and CO2 at 25 C
𝐶 𝐻 𝑂 𝑠 6𝑂 𝑔 → 6𝐶𝑂 𝑔 6𝐻 𝑂 𝑙
Calorimetric measurements give ∆ 𝑈=  2808 kJ mol-1 and ∆ 𝑆= 259.1
J K-1mol-1 at 25 C.
(a) How much of this energy change can be extracted as heat
(b) How much work can be extracted from glucose metabolism
performed reversibly.

12. Thermodynamic Relations for a System In Equilibrium
6 Basic Equations
(4.25)
(4.26)
(4.27)
(4.28)
(4.29)
(4.30)
The heat capacities 𝐶 and 𝐶 have alternative expressions that are also basic
equations.
(4.31)
𝐶 , 𝐶  Key properties –
rate of change of U, H & S
The Gibbs Equations
(4.33)
(4.34)
(4.35)
(4.36)
Relation between 𝐶 ,  (thermal expansivity or cubic expansion
coefficient), and κ (kappa - isothermal compressibility)
𝐶 𝑇, 𝑃
𝛼 𝑇, 𝑃 ≡
1
𝑉
𝜕𝑉
𝜕𝑇
κ 𝑇, 𝑃 ≡
1
𝑉
𝜕𝑉
𝜕𝑃
𝜕𝑃
𝜕𝑇
𝛼
κ
Solid  𝛼 = 10-5 to 10-4 K-1
Liquid  𝛼 = 10-3.5 to 10-3 K-1
Gases  estimated (ideal-gas)  1/T
𝛼 = 10-2 to 10-3 K-1
Solid  κ = 10-6 to 10-5 atm-1
Liquid  κ  10-4 atm-1
Gases  estimated (ideal-gas)
κ = 1 atm-1 (1 atm)
κ = 0.1 atm-1 (10 atm)
  and κ  how fast the V of a substance
increases with T and decreases with P.
 The quantities 𝛼 and κ can be used to find
the V change produced by a change in T or P.
(4.39)
The Euler Reciprocity Relations
If 𝑍＝𝑓 𝑥，𝑦 and 𝑍 has continuous second partial derivatives, then
(4.40)
where we defined the functions 𝑀 and 𝑁 as
(4.41)
the order of partial differentiation does not matter:
(4.42)
Hence eqs. (4.40) to (4.42) give
(4.43)
Euler reciprocity relation

13. The Maxwell Relations
(Application of Euler relation to Gibss equations)
(4.44)
(4.45)
• We now find the dependence of U, H, S and G on the variables of the
system.
• The most common independent variables are T and P.
• We can relate the T and P variations of H, S, and G to the measurable 𝐶 ,
, and κ
Dependence of State Functions on T, P, and V
Volume dependence of U
(4.47)
the desired expression for in terms of easily measured properties
Temperature Dependence of U
Temperature Dependence of H
Pressure Dependence of H
(4.48)
Temperature Dependence of S
Pressure Dependence of S
(4.49)
(4.50)
Temperature and Pressure Dependences of G
(4.51)
Joule–Thomson Coefficient
Heat-Capacity Difference
Measurement of the temperature change ∆𝑇 𝑇 𝑇 in the Joule–
Thomson experiment gives ∆𝑇/∆𝑃 at constant H.
(2.64)
𝜇  ratio of infinitesimal changes
in two intensive properties
Substitution this coefficient to Eq (4.48) gives
(4.52)
From heat capacity relation (2.61)
Substitution this relation to Eq. (4.47) and by using  definition (Eq. 4.39) gives
(4.53)

14. Example
Questions & Exercises