Tài liệu trình bày về các phép toán với phân số, bao gồm cả việc xác định hai số có tầm bằng 0 và phương pháp cộng, trừ phân số. Nội dung bao gồm ví dụ minh họa và các quy tắc liên quan đến việc tính toán phân số. Ngoài ra, tài liệu cũng đề cập đến việc phải kiểm tra các đặc điểm của các số nguyên và tính chất của phân số.



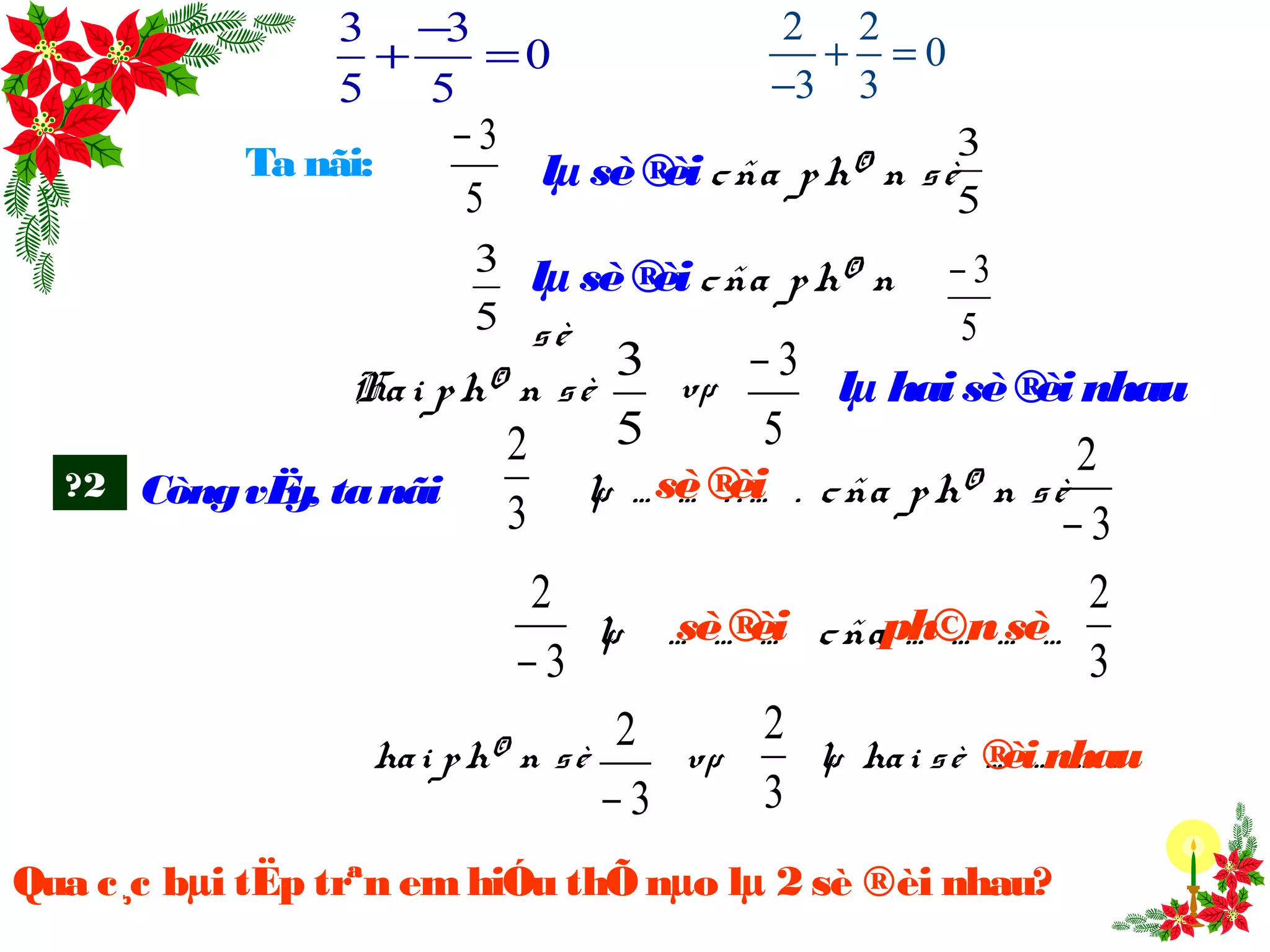







![TÝnh:?4
;
2
1
5
3 −
− ;
3
1
7
5
−
−
;
4
3
5
2 −
−
−
.
6
1
5−−
10
11
10
5
10
6
2
1
5
3
2
1
5
3
=+=+=
−
−
21
22
21
)7(15
21
7
21
15
3
1
7
5
3
1
7
5 −
=
−+−
=
−
+
−
=
−
+
−
=−
−
20
7
20
158
20
15
20
8
4
3
5
2
4
3
5
2
=
+−
=+
−
=+
−
=
−
−
−
( )30 11 5 1 30 1 31
5
6 1 6 6 6 6 6
− + −− − − −
− − = + − = + = = ÷
Lêi gi¶i:Lêi gi¶i: Hai häc sinh thùcHai häc sinh thùc
hiÖn [ ?4]hiÖn [ ?4]](https://image.slidesharecdn.com/pheptruphanso-150504193021-conversion-gate02/75/Phep-tru-phan-so-13-2048.jpg)