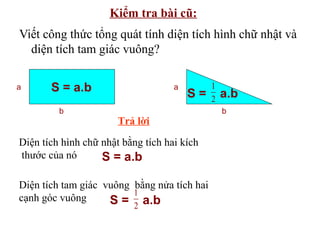
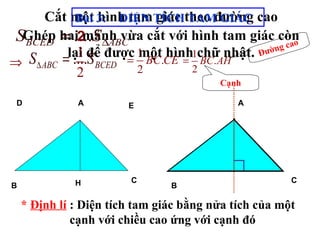
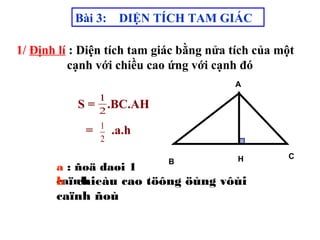
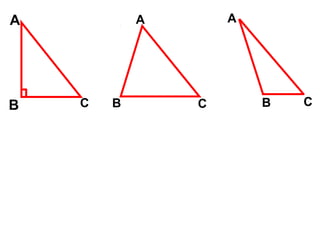
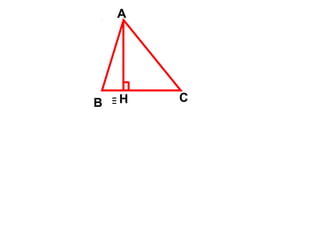
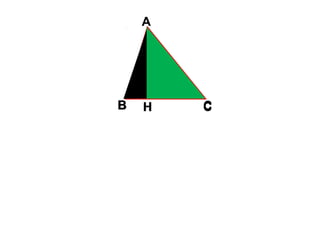
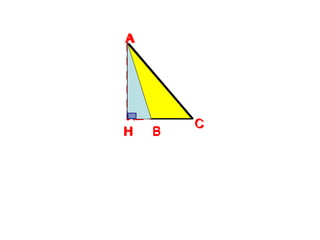
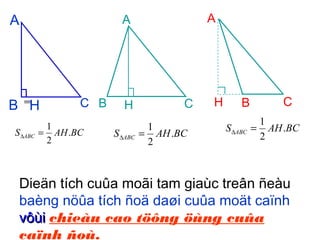
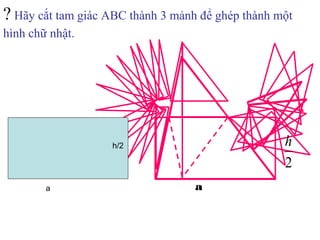
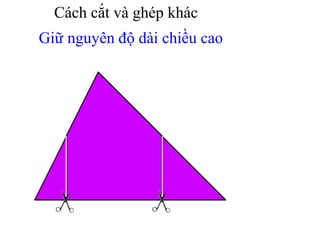
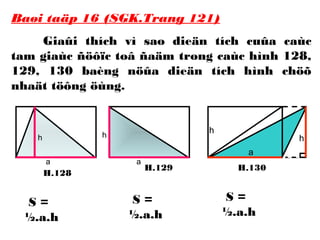
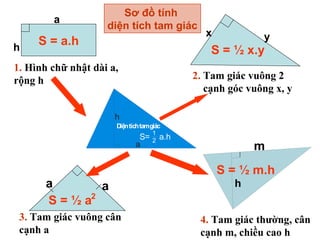
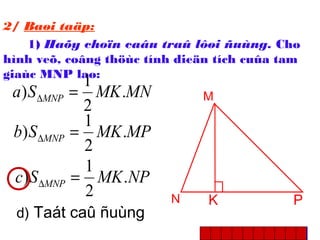
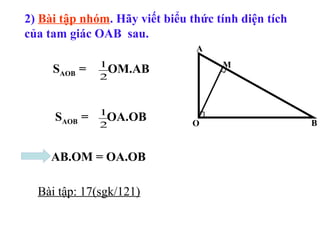
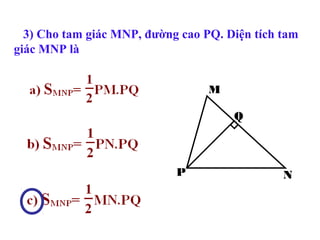
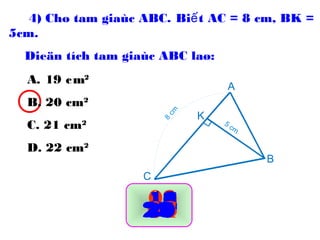
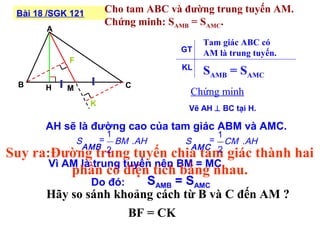
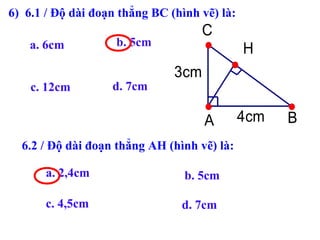
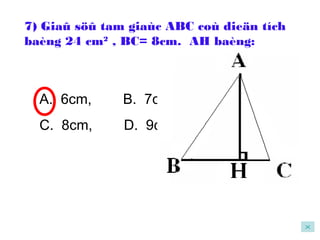
Tài liệu hướng dẫn giáo viên và học sinh về cách tính diện tích hình chữ nhật và tam giác vuông, với các công thức cụ thể như s = a.b và s = 1/2.a.h. Nó cũng trình bày các bài tập minh họa và yêu cầu học sinh vận dụng các kiến thức để giải quyết bài tập về diện tích tam giác. Cuối cùng, tài liệu nhấn mạnh tầm quan trọng của việc hiểu và chứng minh các công thức này.

1. CHÀO MỪNG CÁC THẦY CÔ GIÁO
VỀ DỰ GIỜ TIẾT HỌC HÔM NAY

2. Kiểm tra bài cũ:
Viết công thức tổng quát tính diện tích hình chữ nhật và
diện tích tam giác vuông?
Trả lời
Diện tích hình chữ nhật bằng tích hai kích
thước của nó S = a.b
a
b b
a
Diện tích tam giác vuông bằng nửa tích hai
cạnh góc vuông S = a.b
1
2
S = a.b S = a.b
1
2

3. Cắt một hình tam giác theo đường cao
Ghép hai mảnh vừa cắt với hình tam giác còn
lại để được một hình chữ nhật.
A
B
C
A
B
C
E
H
D
....BCED ABCS S∆= 2
⇒ ....ABC BCEDS S∆ = 1
2
1
.
2
BC CE=
1
.
2
BC AH=
Cạnh
Đường cao
* Định lí : Diện tích tam giác bằng nửa tích của một
cạnh với chiều cao ứng với cạnh đó
Bài 3: DIỆN TÍCH TAM GIÁC

4. Bài 3: DIỆN TÍCH TAM GIÁC
A
B
CH
1/ Định lí : Diện tích tam giác bằng nửa tích của một
cạnh với chiều cao ứng với cạnh đó
S = .BC.AH
1
2
= .a.h1
2
a : ñoä daøi 1
caïnhh : chieàu cao töông öùng vôùi
caïnh ñoù

5. A
CB
A
B C CB
A

6. H
A
B C≡

7. A
B CHB HH
AA
C

8. H
A
C
B
A
C
H
A
BH

9. A
≡ CB H
BCAHS ABC .
2
1
=∆
A
B CH CB
A
H
BCAHS ABC .
2
1
=∆
Dieän tích cuûa moãi tam giaùc treân ñeàu
baèng nöûa tích ñoä daøi cuûa moät caïnh
vôùivôùi chieàu cao töông öùng cuûa
caïnh ñoù.
BCAHS ABC .
2
1
=∆

10. a
2
h
? Hãy cắt tam giác ABC thành 3 mảnh để ghép thành một
hình chữ nhật.
a
h/2

11. Cách cắt và ghép khác
Giữ nguyên độ dài chiều cao

12. H·y c¾t mét tamgi¸c thµnh ba m¶nh ®Ó
ghÐp l¹i thµnh mét h×nh ch÷ nhËt.

13. h
a
H.128
H.129 H.130
h
a
h
a
h
Baøi taäp 16 (SGK.Trang 121)
Giaûi thích vì sao dieän tích cuûa caùc
tam giaùc ñöôïc toâ ñaäm trong caùc hình 128,
129, 130 baèng nöûa dieän tích hình chöõ
nhaät töông öùng.
S =
½.a.h
S =
½.a.h
S =
½.a.h

14. Diệntíchtamgiác
S= a.h
1
2
a
h
3. Tam giác vuông cân
cạnh a
S = a.h
1. Hình chữ nhật dài a,
rộng h
4. Tam giác thường, cân
cạnh m, chiều cao h
2. Tam giác vuông 2
cạnh góc vuông x, y
x y
a
h
m
h
S = ½ x.y
S = ½ a2
S = ½ m.h
a a
Sơ đồ tính
diện tích tam giác

15. M
N PK
2/ Baøi taäp:
1) Haõy choïn caâu traû lôøi ñuùng. Cho
hình veõ, coâng thöùc tính dieän tích cuûa tam
giaùc MNP laø:
MNMKSa MNP .
2
1
) =∆
MPMKSb MNP .
2
1
) =∆
NPMKSc MNP .
2
1
) =∆
d) Taát caû ñuùng

16. O B
A
M
2) Bài tập nhóm. Hãy viết biểu thức tính diện tích
của tam giác OAB sau.
SAOB = OA.OB
AB.OM = OA.OB
1
2
1
2
SAOB = OM.AB
Bài tập: 17(sgk/121)

17. N
M
P
Q
3) Cho tam giác MNP, đường cao PQ. Diện tích tam
giác MNP là

18. A. 19 cm2
B. 20 cm2
C. 21 cm2
D. 22 cm2
00091011121615141317181920080706050403020129302827262524232221
A
B
C
K
5 cm
8
cm
4) Cho tam giaùc ABC. Bi t AC = 8 cm, BK =ế
5cm.
Dieän tích tam giaùc ABC laø:

19. B M C
A
Bài 18 /SGK 121
Tam giác ABC có
AM là trung tuyến.
SAMB = SAMC
GT
KL
Chứng minhH
Vẽ AH ⊥ BC tại H.
AH sẽ là đường cao của tam giác ABM và AMC.
Vì AM là trung tuyến nên BM = MC.
Do đó: SAMB = SAMC
Suy ra:Đường trung tuyến chia tam giác thành hai
phần có diện tích bằng nhau.
Cho tam ABC và đường trung tuyến AM.
Chứng minh: SAMB = SAMC.
F
K
Hãy so sánh khoảng cách từ B và C đến AM ?
AHBMS
AMB
.
2
1
= AHCMS
AMC
.
2
1
=
BF = CK

20. a. 6cm
4cm
3cm
H
A B
C
c. 12cm d. 7cm
6.2 / Độ dài đoạn thẳng AH (hình vẽ) là:
a. 2,4cm b. 5cm
c. 4,5cm d. 7cm
b. 5cm
6) 6.1 / Độ dài đoạn thẳng BC (hình vẽ) là:

21. 7) Giaû söû tam giaùc ABC coù dieän tích
baèng 24 cm2
, BC= 8cm. AH baèng:
A. 6cm, B. 7cm
C. 8cm, D. 9cm


22. KiÕn thøc cÇn n¾m v÷ng :
 Coâng thöùc tính dieän tích tam giaùc
Trong
ñoù:
a: ñoä daøi 1
caïnhh: chieàu cao töông öùng
vôùi caïnh ñoù
 Bieát chöùng
minh coâng thöùc
tính dieän tích tam
giaùc
Tröôøng hôïp tam giaùc
nhoïn
Tröôøng hôïp tam giaùc
vuoâng
Tröôøng hôïp tam giaùc
tuø
 Bieát vaän duïng ñeå laøm baøi
haS .
2
1
=
h
a

23. Hướng dẫn học ở nhà
 Nắm vững công thức tính diện tích
tam giác và cách chứng minh định lý
 Bài tập về nhà: 20, 21, 22, 23
SGK trang 122, 123