Downloaded 31 times
Uploaded byUmi Jauhar
Pecahan nota oll-wat cerita
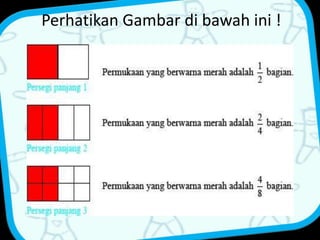
Dokumen ini membahas tentang pecahan, termasuk definisi, jenis-jenis pecahan, serta operasi matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian yang melibatkan pecahan dan desimal. Ada juga contoh soal untuk memperjelas penerapan konsep dan cara menghitung pecahan dalam kehidupan sehari-hari. Di samping itu, terdapat penjelasan tentang perbandingan dan konversi satuan suhu serta jarak.
More Related Content
![Tekpend.pptx.updated [recovered]](https://cdn.slidesharecdn.com/ss_thumbnails/tekpend-150521232958-lva1-app6892-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Pecahan nota oll-wat cerita
Pecahan nota oll-wat cerita
- 1.
- 2. PENGENALAN PECAHAN Pecahanadalah beberapa bagian dari keseluruhan contoh:
- 3. Pecahan terjadi karenasuatu benda dibagi menjadi beberapa bagian sama besar. Bagian-bagian itu mempunyai nilai pecahan
- 4. Pecahan dapat dibentukdari operasi pembagian 1/2 = 1 : 2 3/6 = 3 : 6
- 5. Pecahan campuran merupakanbentuk penyederhanaan dari pecahan biasa yang memiliki pembilang yang nilainya lebih besar daripada penyebutnya
- 6. Mengubah Pecahan menjadi Pecahan Yang Senilai
- 7. Perhatikan Gambar dibawah ini !
- 9. Menentukan Pecahan –Pecahan yang Senilai Perhatikan garis bilangan berikut ini dengan baik ! 0 2 1 2 2 2 3 2 4 2 0 3 0 4 0 5 0 6 1 3 1 4 1 5 1 6 2 6 2 5 2 3 2 4 3 4 3 6 4 6 3 5 3 3 4 4 5 5 5 6 6 6 6 5 7 6 4 3 5 4 6 4 9 6 8 5 5 3 10 6 7 4 9 5 6 3 8 4 11 6 10 5 12 6
- 10. Menentukan Pecahan SenilaiTanpa Garis Bilangan Contoh : Cara mengerjakannyaadalah: PembilangandanPenyebut di bagidenganbilangan yang samayaitu 3, makahasilnyaadalah 1 2 3 = 3:3 = 1 6 6:3 2
- 11.
- 13. 0 ¼ ½¾ 1
- 14. Pecahan Desimal a.Satukoma dua empat b.Satu dua puluh empat perseratus c.Satu koma dua puluh empat 1,24 Dibaca apa??
- 15. Contoh: 1 10 3 100 0,1 0,03
- 16. , Nilai tempatsatuan Nilai tempat persepuluh Nilai tempat perseratusan
- 18. Nilai Pecahan atauPersentase dari Besaran Tertentu Contoh : Wulan membawa air minum 250 ml ke sekolah. Jika wulan meminum 2/5 bagian diminum sebelum masuk sekolah dan sisanya diminum setelah masuk sekolah. Berapa ml air yang di minum setelah masuk sekolah? Jawab: Air yang diminum setelah masuk sekolah : 5/5 -2/5=3/5 Air yang diminum setelah masuk : 3/5 × 250ml = 150 ml Atau 1/5 ×250ml = 100ml Jadi, air yang diminum Wulan setelah masuk : 250ml -100ml = 150ml
- 19. OPERASI PENJUMLAHAN PADA PECAHAN • Penjumlahan Dua Pecahan Biasa Berpenyebut Sama • Penjumlahan Dua Pecahan Biasa Berpenyebut Beda • Penjumlahan Pecahan Biasa dan Pecahan Campuran • Penjumlahan Pecahan Campuran dan Pecahan Campuran • Penjumlahan pada Pecahan Desimal
- 21. Penjumlahan Dua PecahanBiasa Berpenyebut Beda Untuk menjumlahkan dua pecahan berpenyebut beda, kalikan penyebutnya lalu dikalikan silang pembilangnya. + =
- 22. • Ubah pecahancampuran menjadi pecahan biasa. • Samakan penyebut-penyebutnya dengan menggunakan KPK • Sederhanakan sampai bentuk yang paling sederhana
- 23. • Ubah pecahancampuran menjadi pecahan biasa. • Samakan penyebut-penyebutnya dengan menggunakan KPK. • Sederhanakan sampai bentuk yang paling sederhana.
- 24. • Penjumlahan PecahanDesimal Persepuluh • Letakkan satuan lurus dengan satuan , persepuluh lurus dengan persepuluh. • Jumlahkan seperti bilangan asli secara bersusun. • Letakkan koma hasil penjumlahan harus lurus.
- 26. PENGURANGAN 1. Penguranganpada bilangan asli dengan pecahan biasa 2. Pengurangan pada bilangan asli dengan pecahan campuran 3. Pengurangan pada pecahan biasa dengan pecahan biasa 4. Pengurangan pada pecahan biasa dengan pecahan campuran 5. Pengurangan pada pecahan campuran dengan pecahan campuran 6. Pengurangan dengan pecahan desimal
- 27. Perkalian pada pecahan 1. Perkalian pada bilangan asli dengan pecahan biasa 2. Perkalian pada bilangan asli dengan pecahan campuran 3. Perkalian pada pecahan biasa dengan pecahan biasa 4. Perkalian pada pecahan biasa dengan pecahan campuran 5. Perkalian pada pecahan campuran dengan pecahan campuran 6. Perkalian dengan pecahan desimal
- 28. • Perkalian diubah menjadi penjumlahan berulang • Bilangan asli dikalikan dengan pembilang, penyebut tetap
- 29. Perkalian pada bilanganasli dengan pecahan campuran Cara I : 1. Pecahan campuran di ubah menjadi pecahan biasa 2. Lakukan perkalian bilangan asli dengan pecahan biasa yang diperoleh Cara II: 1. Pecahan dipisahkan menjadi bagian pecahan dan bagian bulat 2. Bilangan asli dikalikan dengan bagian bulat ditambah bilangan asli dikalikan bagian pecahan
- 30. Perkalian pada pecahanbiasa dengan pecahan biasa Pembilang pembilang Penyebut penyebut
- 31. Perkalian pada pecahanbiasa dengan pecahan campuran 1. Pecahan campuran diubah menjadi pecahan biasa 2. Kalikan dua pecahan biasa yang diperoleh
- 32. Perkalian pada pecahan campuran dengan pecahan campuran • Kedua pecahan campuran diubah menjadi pecahan biasa. • Kalikan pecahan biasa dengan pecahan biasa yang diperoleh
- 33. Perkalian pada pecahandesimal Contoh : 8,4 3,7 5 8 8 2 5 2 + 3 1,0 8 1 tempat desimal 1 tempat desimal (1+1) = 2 tempat desimal Jadi, 8,4 3,7 = 31,08
- 34. Pembagian Pecahan •Kegiatan Belajar 1: Pembagian Pecahan Biasa. • Kegiatan Belajar 2: Pembagian Pecahan Campuran. • Kegiatan Belajar 3: Pembagian Pecahan Desimal.
- 35. Bilangan asli dibagipecahan biasa Contoh : Kakak mempunyai 2 m pita dan akan dibuat bunga. Masing-masing bunga memerlukan pita ¼ m. Berapa banyak bunga yang dapat dibuat oleh kakak?
- 36. Pecahan biasa dibagidengan bilangan asli Adik mempunyai ½ batang coklat yang akan diberikan kepada 3 temannya dan masing-masing teman harus mendapat coklat yang sama banyak. Maka coklat yang diterima setiap teman adik adalah … bagian. Permasalahan di atas dalam kalimat matematika adalah ½ : 3 = ….
- 37. Pecahan biasa dibagidengan pecahan biasa Kakak mempunyai ¾ m pita yang akan dibuat hiasan. Setiap satu hiasan memerlukan pita ¼ m. Berapa banyak hiasan yang dapat dibuat? Dalam kalimat matematika adalah ¾ : ¼ = …
- 38. Pembagian pecahan campuran • Ibu membeli beras 30 kg. Setiap hari ibu menanak nasi untuk keluarganya sebanyak 1 ½ kg. Berapa hari beras tersebut dapat memenuhi kebutuhan ibu?
- 39.
- 40. Misalnya m =boneka kiri p = boneka kanan Perbandingan banyak jumlah boneka kiri dan banyak boneka kanan adalah m : p = 1: 4
- 41. Dari pernyataantersebut, kitadapatmenentukanperbandingan-perbandinganberikut. • Perbandinganbanyakbonekakiriterhadapjumlahboneka 풃풂풏풚풂풌풏풚풂 풃풐풏풆풌풂 풌풊풓풊 adalah 풋풖풎풍풂풉 풃풐풏풆풌풂 = 풎 풎+풑 = ퟏ ퟒ+ퟓ = ퟏ ퟗ • Perbandinganbanyakbonekakananterhadapjumlah bola 풃풂풏풚풂풌풏풚풂 풃풐풍풂 풌풂풏풂풏 adalah 풋풖풎풍풂풉 풃풐풏풆풌풂 = 풑 풎+풑 = ퟒ ퟒ+ퟓ = ퟒ ퟗ • Perbandinganbanyakbonekakiriterhadapselisihbonekakirida 풃풂풏풚풂풌 풃풐풏풆풌풂 풌풊풓풊 nkananadalah 풔풆풍풊풔풊풉 풃풐풏풆풌풂 = 풎 풑−풎 = ퟏ ퟓ−ퟏ = ퟏ ퟒ • Perbandinganbanyakbonekakananterhadapselisihbonekakan andanbonekakiriadalah 풃풂풏풚풂풌 풃풐풏풆풌풂 풌풂풏풂풏 풔풆풍풊풔풊풉 풃풐풏풆풌풂 = 풑 풑−풎 = ퟒ ퟓ−ퟏ = ퟒ ퟒ
- 42. Membandingkan pecahan berpenyebutsama 1. ퟓ ퟖ ퟑ ퟖ ….. pembilang kedua pecahanadalah 5 dan 3 ퟓ ퟖ ퟑ ퟖ > ퟓ > ퟑ ퟓ ퟖ Jadi ퟑ ퟖ > Perhatikan pembilang kedua pecahan berpenyebut sama
- 43. Membandingkan pecahan berpenyebuttidak sama 1 3 2 4 ….. • Cara 1: menggunakangarisbilangan 0 1 3 2 3 1 0 1 4 2 4 3 4 1
- 44. ퟏ ퟑ Darigarisbilangan di atas,terlihatbahwa ퟐ ퟒ terletak di sebelahkiri jadi ퟏ ퟑ ퟐ ퟒ < • Cara 2: menyamakanpenyebut Carikpkdaripenyebut kedua pecahan.samakanpenyebut kedua pecahandengankpk.kpkdari 3 dan 4 adalah 12.penyebut kedua pecahan di ubahmenjadi 12. ퟏ ퟏ×ퟒ ퟒ = = 3 dikalikan 4 agar menjadi 12 ퟑ ퟑ×ퟒ ퟏퟐ ퟐ ퟒ = ퟐ×ퟑ ퟒ×ퟑ = ퟔ ퟏퟐ 4 dikalikan 3 agar menjadi 12 ퟒ ퟏퟐ ퟔ ퟏퟐ < 4 < 6 Jadi ퟏ ퟑ ퟐ ퟒ < Gunakan kpk untuk menyamakan penyebut kedua pecahan
- 45. PerbandinganSenilai • Untukmemahamiperbandingansenilai, pelajarilahcontohberikut. Misalkandalam 4 hari, Budi bekerjaselama 28 jam. Berapa jam Budi bekerjaselama 5 hari? Cara penyelesaiannyaadalahsebagaiberikut. 4 hari : 5 hari = 28 jam : t, t = lamanya Budi bekerjaselama 5 hari ퟒ ퟓ = ퟐퟖ 풕 ingatperkaliansilang!!!! ퟐퟖ×ퟓ ퟒ t = t = 35 Jadi, lamanya Budi bekerjaselama 5 hariadalah 35 jam.
- 46. Suhu • Reamur(R): Celsius (C ): Fahreinheit (F) = 4: 5: 9 (+ 32) • Contoh • TermometerReamurmenunjukansuhu 80, berapaderajatsuhupadatermometercelciusdanfahreinheit? • Celsius = ퟓ ퟒ × 80 = 100 • Fahreinheit = ퟗ ퟒ × 80 = 212 • Fahreinheit = 194 • Celsius =…….. • Reamur =………
- 47. • Celsius = ퟓ ퟗ × (194-32) = ퟓ ퟗ × 162 =90 • Reamur = ퟒ ퟗ × (194 - 32) ퟒ ퟗ = × 162 =72
- 48. Skala Skala= jarak sebenarnya pada peta: jarak sebenarnya Jarak kota A ke kota B di sebuah peta 8 cm pada peta tertulis skala 1: 500.000 , Berapa jarak sebenarnya? Dik : jarak di peta 8 cm Skala pada peta : 1: 500.000 Dit : jarak sesungguhnya kota A ke kota B ? Penyelesaian 1 cm pada peta = 500.000 cm pada jarak sebenarnya jadi jarak sebenarnya kota A dengan kota B adalah 8 × 500.000 = 4.000.000 cm =40 km