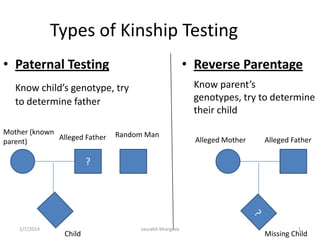
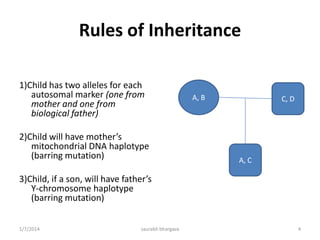
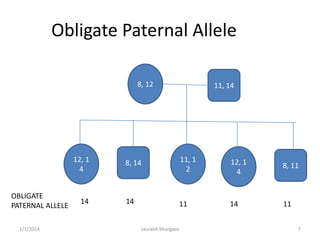
1. Paternity testing involves analyzing genetic markers from the mother, child, and alleged father to determine paternity. Key genetic concepts include obligate paternal alleles, paternity index, and combined paternity index. 2. Mathematical calculations are used to either exclude a man from paternity or provide an estimated probability of paternity. This probability takes into account the genetic evidence from testing as well as a prior probability of paternity. 3. Multiple genetic systems are tested, and the paternity index for each system is multiplied to obtain the combined paternity index, which provides a stronger measure of genetic evidence for or against paternity.

1. Overview
• Loci/Allele
• Obligate Alleles
• Paternity Index (PI)
• Combined Paternity Index (CPI)
• Prior probability (pp)
• Probability of Paternity (POP)
9/27/2016 1saurabh bhargava

2. Types of Kinship Testing
• Paternal Testing
Know child’s genotype, try
to determine father
• Reverse Parentage
Know parent’s genotypes,
try to determine their child
?
Random Man
Alleged Mother
Missing ChildChild
Mother (known
parent)
Alleged Father Alleged Father
9/27/2016 2saurabh bhargava

3. Genetic Markers
• Half of a child's genetic material (alleles) come from
the mother, while the other half is contributed by the
father.
• A series of genetic systems (loci) are analyzed in an
attempt to ascertain the biological father of a child.
• Each genetic system in a person has two allele, these
alleles are numerically labeled.
• In paternity testing, the alleles from the child are
compared to those of the "parents" to determine if it is
possible for either or both parents to have contributed
the particular alleles present in the child.
9/27/2016 3saurabh bhargava

4. How
• DNA (alleles) from the mother, child, and
alleged father are extracted, amplified, and
identified.
• A series of mathematical calculations are then
used to either completely exonerate an
accused man or provide an estimate of
probability of his paternity (POP).
9/27/2016 4saurabh bhargava

5. Mendelian Segregation
Rules of Inheritance:
1. Child has two alleles for each
autosomal marker (one from
mother and one from
biological father)
2. Child will have mother’s
mitochondrial DNA
haplotype (barring mutation)
3. Child, if a son, will have
father’s Y-chromosome
haplotype (barring mutation)
C, D
A, C
A, B
9/27/2016 5saurabh bhargava

6. Conti..
• For instance, assume that a child has a 10 and 11 allele for a
particular genetic system and the child's mother is known to
possess a 10 and a 12 allele for this system.
• The mother must have contributed the 10 allele and the 11 allele
must be paternal. In this example, any man who does not possess
an 11 allele could not be the child's father (barring the possibility of
mutation that converts one allele to another - something that is
unlikely but can be taken into consideration if needed).
• In the event that a man is not excluded, the likelihood that a
randomly chosen man might also be able to provide the allele in
question to the child can be determined by examining the allelic
frequencies from a relevant population database.
9/27/2016 6saurabh bhargava

7. Obligate Paternal Allele
• The alleles the actual father MUST have
• Compare the child to the mom
• Whatever allele the mom does not have is the
obligate paternal allele
• If mom and dad share alleles there will be less
information
• More markers you type –eventually you will
find unique alleles
9/27/2016 7saurabh bhargava

8. Obligate Paternal Allele
12,
14
12,
14
11,
12
8, 12
8, 14 8, 11
11, 14
OBLIGATE
PATERNAL ALLELE
14 1114 1114
9/27/2016 8saurabh bhargava

9. Obligate Paternal Allele
8, 12
12,
12
12,
12
11,
12
?
8, 118, 12
Obligate Paternal
Allele 12 EITHER
8 OR12
111211
WHAT GENOTYPE MUST THE TRUE FATHER HAVE???
IF THERE IS ONE FATHER FOR ALL THE CHILDREN THEN IT HAS TO BE 11, 12
9/27/2016 9saurabh bhargava

10. Paternity Index
• The paternity index (PI) compares the likelihood that a
genetic marker (allele) that the alleged father (AF) passed
to the child to the probability that a randomly selected
unrelated man of similar ethnic background could pass the
allele to the child.
• This is presented in the formula X/Y, where X is the chance
that the AF could transmit the obligate allele and Y is the
chance that some other man of the same race could have
transmitted the allele.
• X is assigned the value of 1 if the AF is homozygous for the
allele of interest and 0.5 if the AF is heterozygous.
9/27/2016 10saurabh bhargava

11. Conti..
• PI = paternity index
• Ratio of the two probabilities:
____p(AF is the father)___
p(A random man is the father)
• Ratio then represents how much better the data (genotypes) fits
with the hypothesis that the AF is the real father
• Larger ratio  more evidence that this man is the real father
9/27/2016 11saurabh bhargava

12. Two possible results
1.Inclusion:
• Tested man, Alleged Father, could be this
child’s father
2. Exclusion:
• There is no way that the AF could be this
child’s father
9/27/2016 12saurabh bhargava

13. Combined Paternity Index
• When multiple genetic systems are tested, a PI is
calculated for each system.
• The genetic systems are inherited independently, the
Combined Paternity Index (CPI) is the product of
system PIs.
or
• The combined paternity index (CPI) is determined by
multiplying the individual PIs for each locus tested.
• This value is referred to as system PI.
9/27/2016 13saurabh bhargava

14. Combined Paternity Index
• The CPI is an odds ratio that indicates how many times more likely it
is that the alleged father is the biological father than a randomly
selected unrelated man of similar ethnic background.
• The CPI is a measure of the strength of the genetic evidence.
• The CPI is based solely on genetic evidence.
• Theoretically the range of CPI is 0- ∞ (zero to infinity)
– CPI=1; no information
– CPI<1; the genetic evidence is more consistent with non-paternity
than paternity
– CPI>1; the genetic evidence supports the assertion that the tested
man is the father
9/27/2016 14saurabh bhargava

15. Probability of Paternity
• The probability of paternity is the measure of
strength of one’s belief in the hypothesis that the
tested man is the father.
• The correct probability must be based on all the
evidences of the case.
• The non-genetic evidence comes from the
testimony of mother, tested man & other
witnesses.
• The genetic evidence comes from DNA paternity
tests.
9/27/2016 15saurabh bhargava

16. Probability of Paternity
• The probability of paternity (W) is based upon Baye’s
Theorem, which provides a method for determining a
posterior probability based upon the genetic results of testing
the mother, child and alleged father.
• In order to determine the probability of paternity, an
assumption must be made (before testing) as to the prior
probability that the tested man is the true biological father.
• The prior probability of paternity is the strength of one’s
belief that the tested man is the father based only on the
non-genetic evidences.
9/27/2016 16saurabh bhargava

17. Probability of Paternity
• To convert the genetic evidence to a probability of paternity (POP) it is necessary
to use the Baysian theorem.
• This is a formula that tests the hypothesis that the accused is the biological father
of the child.
– For example, a POP of 99% reflects a 99% probability that the hypothesis is correct and a 1%
probability that it is not.
• The CPI is used in the Bayes formula along with another variable called a prior
probability (PP).
– Testing labs typically use a value of 0.5 for the PP assuming this is a neutral, unbiased value.
• The Baysian formula is
• CPI×PP
{CPI×PP+(1-PP)}
9/27/2016 17saurabh bhargava

18. Probability of Paternity
• With a prior probability of 0.5, the
– Probability of paternity(w) =
CPI X 0.5____
{CPI X 0.5+(1-0.5)}
_CPI_
(CPI+1)
9/27/2016 18saurabh bhargava

19. PRIOR PROBABILITY
• If we wishes to assume a prior probability of 50%, then
the (posterior) probability will be “x” [whatever figure
is given].
• On the other hand, if we feel that some other prior
probability is appropriate, then the posterior
probability will be somewhat different.
• NOTE: if the report gives a W value with no mention at
all of a prior probability (which is the practice in most
countries), then it is flat misleading.
9/27/2016 19saurabh bhargava

20. PRIOR PROBABILITY
• But the effect of allowing “pp” to vary is often
not material because using DNA tests (CPI) is
usually very large.
• For example, suppose that CPI=100000. Then
the paternity report will probably calculate
W=100000/100001 and report W=99.999%, at
50% prior probability.
9/27/2016 20saurabh bhargava

21. PRIOR PROBABILITY
• Suppose that the defendant presents powerful testimony: the woman is
unreliable and has made many false accusations in the past; he is a
prominent person, a likely target; she admits that full penetration did not
occur and that he failed to ejaculate.
• Suppose that from all of this the judge is persuaded to estimate that if
testimony like this were presented in 500 cases, only about once would
the man be the father and 499 he would have been falsely accused. So
pp=1/500.
• Applying the above formula, we get
– W=99.5%, at 0.02% prior probability.
• The verdict is probably the same whether
W=99.5% or 99.92%.
9/27/2016 21saurabh bhargava

22. PRIOR PROBABILITY
• So while the man is entitled by our system of
jurisprudence to have his say in court, it is
likely that nothing he can say will be
significant compared to the force of the DNA
evidence.
9/27/2016 22saurabh bhargava

23. POSTERIOR ODDS IN FAVOUR OF
PATERNITY
• Posterior odds = CPI X Prior odds
• Prior odds = P/(1-P)
• Posterior odds = CPI X {P/(1-P)}
• If the prior probability of paternity is 0.7, then the prior
odds favoring paternity are 7 to 3 & If a paternity test is
done & CPI is 10,000 then- Posterior Odds in favor of
paternity= 10000x0.7/0.3= 23,333 to 1
9/27/2016 23saurabh bhargava