The document discusses performance improvements in computational tasks using superscalar architectures and SIMD, specifically focusing on the Mandelbrot set calculations on an i5 6600k processor. It details the computational efficiency and optimization techniques for executing mathematical operations, including instruction scheduling and minimizing CPU stalls. The document also presents code snippets demonstrating the implementation of the Mandelbrot algorithm in a high-performance context.

1. Better performance
through Superscalarity
Mårten Rånge

2. How many GigaFlops?
i5 6600K 3.5 GHz
(4x cores)

3. ~224 GigaFlops

4. 64 Flops/cycle

6. Zn+1 = Zn
2 + C (1)
Z0 = C (2)

7. (x,y)

8. (x,y) + (c,d)

9. (x+c,y+d)

10. (x,y)2

11. (x2 - y2,2xy)

12. r
aZk
Z0
2
2a
r2
Z1 = Z0
2 + C
C
|R| = 2
Zl
Zm
Z0
Zn+1 = Zn
2 + C

14. constexpr auto max_iter = 50U;
auto mandelbrot (double cx, double cy) {
auto x = cx ;
auto y = cy ;
auto iter = max_iter;
for (; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
if (x2 + y2 > 4) return iter;
y = 2*x*y + cy ;
x = x2 - y2 + cx ;
}
return iter;
}
r2 = x2 + y2
y
x
r
(x,y)2 = (x2 - y2,2xy)
Zn+1 = Zn
2 + C

15. SIMD

16. a = b+c

17. (a0,a1)=(b0,b1)+(c0,c1)

18. 0 1 2 3
4 5 6 7
4 6 8 10
+

19. AVX
8 flops/instruction

20. constexpr auto max_iter = 50U;
auto mandelbrot (double cx, double cy) {
auto x = cx ;
auto y = cy ;
auto iter = max_iter;
for (; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
if (x2 + y2 > 4) return iter;
y = 2*x*y + cy ;
x = x2 - y2 + cx ;
}
return iter;
}

21. auto mandelbrot (__m256 cx, __m256 cy) {
auto x = cx;
auto y = cy;
int cmp_mask = 0 ;
for (auto iter = max_iter; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
auto r2 = x2 + y2;
auto _4 = float8 (4.0F);
cmp_mask = r2 <= _4;
if (!cmp_mask) return 0;
auto xy = x*y;
y = xy + xy + cy;
x = x2 - y2 + cx;
}
return cmp_mask;
}

22. Minimize CPU stalls

23. opcode Latency Throughput
vmulps 5 1
vaddps 3 1
vsubps 3 1
vcmpps 3 1
vmovmskps 1 1

24. Task<float>

25. auto mandelbrot (__m256 cx, __m256 cy) {
auto x = cx;
auto y = cy;
int cmp_mask = 0 ;
for (auto iter = max_iter; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
auto r2 = x2 + y2;
auto _4 = float8 (4.0F);
cmp_mask = r2 <= _4;
if (!cmp_mask) return 0;
auto xy = x*y;
y = xy + xy + cy;
x = x2 - y2 + cx;
}
return cmp_mask;
}

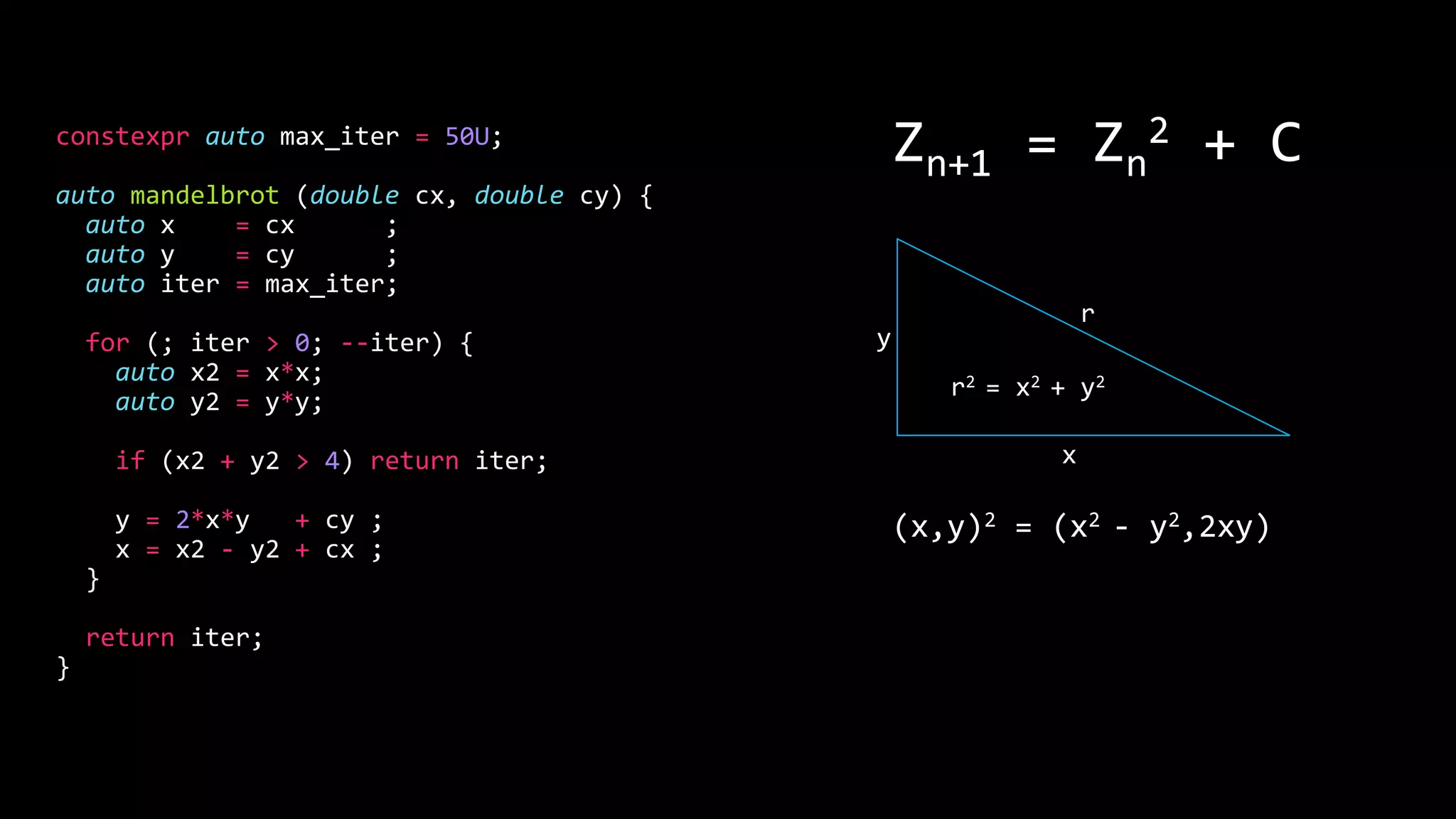
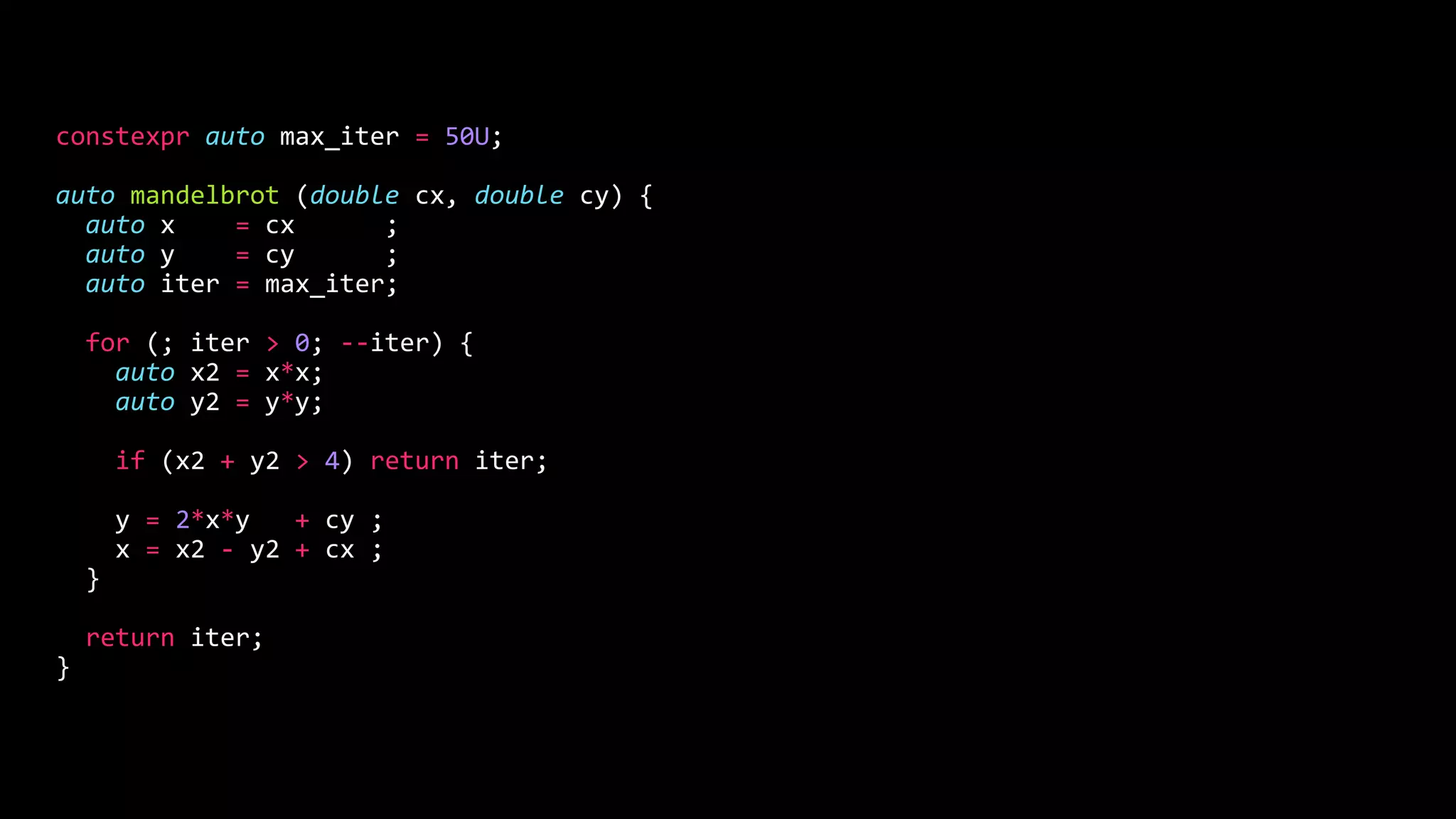
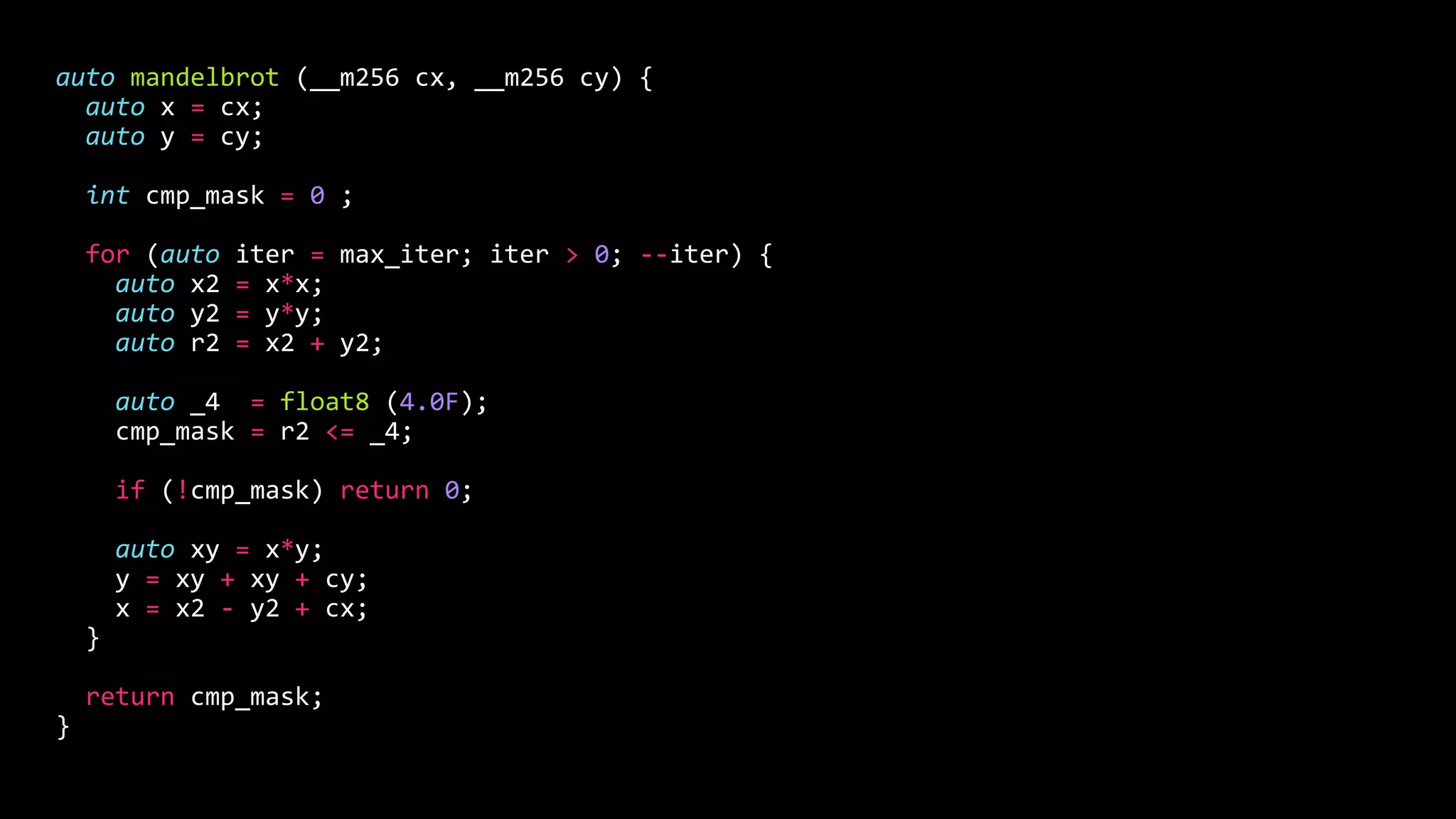
26. x2[0] = x[0]*x[0];
y2[0] = y[0]*y[0];
r2[0] = x2[0] + y2[0];
x2[1] = x[1]*x[1];
y2[1] = y[1]*y[1];
r2[1] = x2[1] + y2[1];
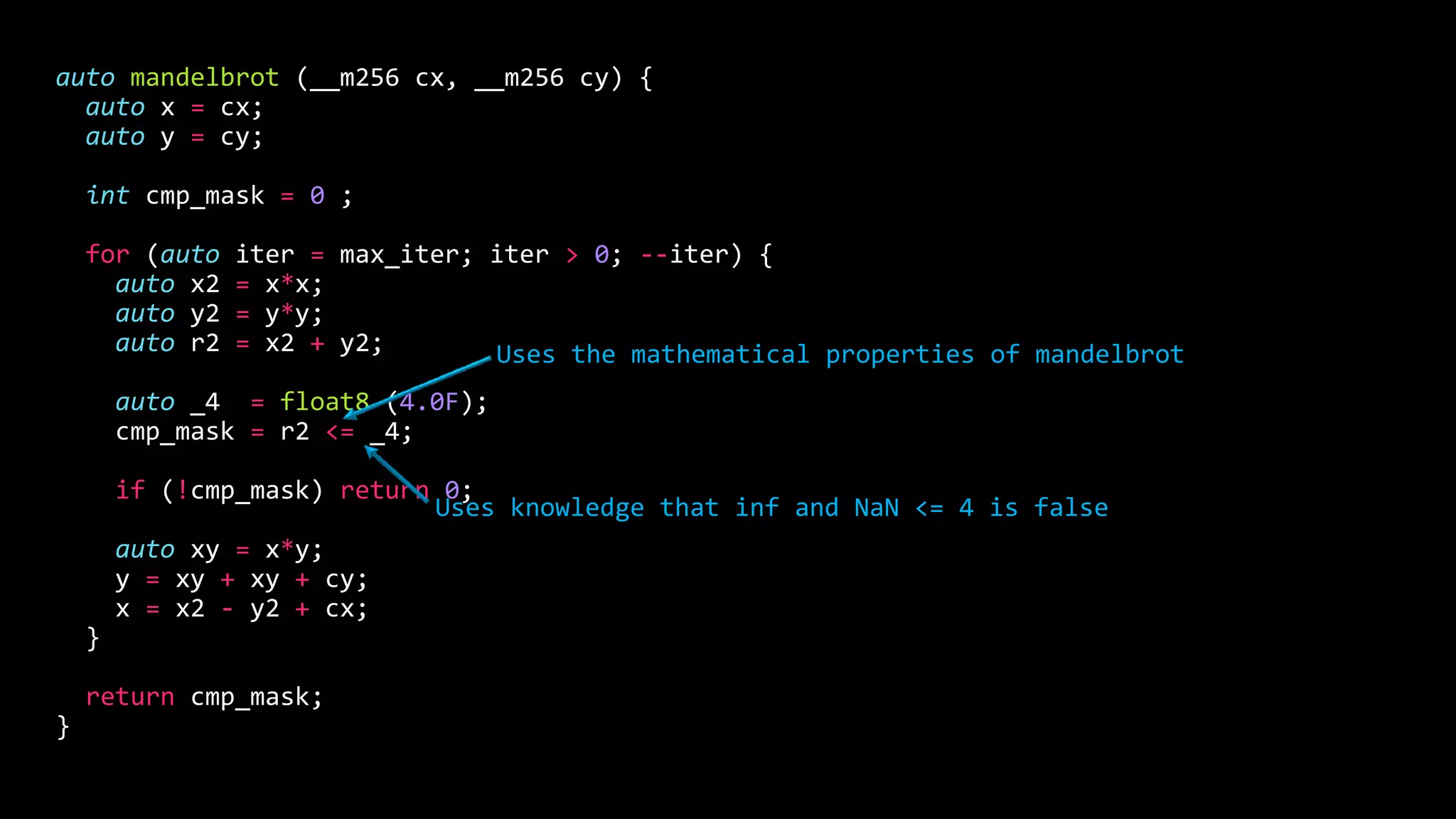
auto _4 = float8 (4.0);
cmp_mask = r2[0] <= _4 | ((r2[1] <= _4) << 8);

27. x2[0] = x[0]*x[0];
y2[0] = y[0]*y[0];
r2[0] = x2[0] + y2[0];
x2[1] = x[1]*x[1];
y2[1] = y[1]*y[1];
r2[1] = x2[1] + y2[1];
r2[0] = x2[0] + y2[0];
auto _4 = float8 (4.0);
cmp_mask = r2[0] <= _4 | ((r2[1] <= _4) << 8);

28. x2[0] = x[0]*x[0]
y2[0] = y[0]*y[0]
r2[0] = x2[0]+y2[0]
x2[1] = x[1]*x[1]
y2[1] = y[1]*y[1]
r2[1] = x2[1]+y2[1]
Instructionqueue
FU
x2[0]
y2[0]
r2[0]
x2[1]
y2[1]
r2[1]
Resultqueue

29. Shouldn’t compilers
do this for us?

30. constexpr auto max_iter = 50U;
auto mandelbrot (double cx, double cy) {
auto x = cx ;
auto y = cy ;
auto iter = max_iter;
for (; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
if (x2 + y2 > 4) return iter;
y = 2*x*y + cy ;
x = x2 - y2 + cx ;
}
return iter;
}

31. auto mandelbrot (__m256 cx, __m256 cy) {
auto x = cx;
auto y = cy;
int cmp_mask = 0 ;
for (auto iter = max_iter; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
auto r2 = x2 + y2;
auto _4 = float8 (4.0F);
cmp_mask = r2 <= _4;
if (!cmp_mask) return 0;
auto xy = x*y;
y = xy + xy + cy;
x = x2 - y2 + cx;
}
return cmp_mask;
}
Uses the mathematical properties of mandelbrot
Uses knowledge that inf and NaN <= 4 is false

32. AVX512
&
Hyper-threading

33. constexpr auto max_iter = 50U;
auto mandelbrot (double cx, double cy) {
auto x = cx ;
auto y = cy ;
auto iter = max_iter;
for (; iter > 0; --iter) {
auto x2 = x*x;
auto y2 = y*y;
if (x2 + y2 > 4) return iter;
y = 2*x*y + cy ;
x = x2 - y2 + cx ;
}
return iter;
}

34. Questions?