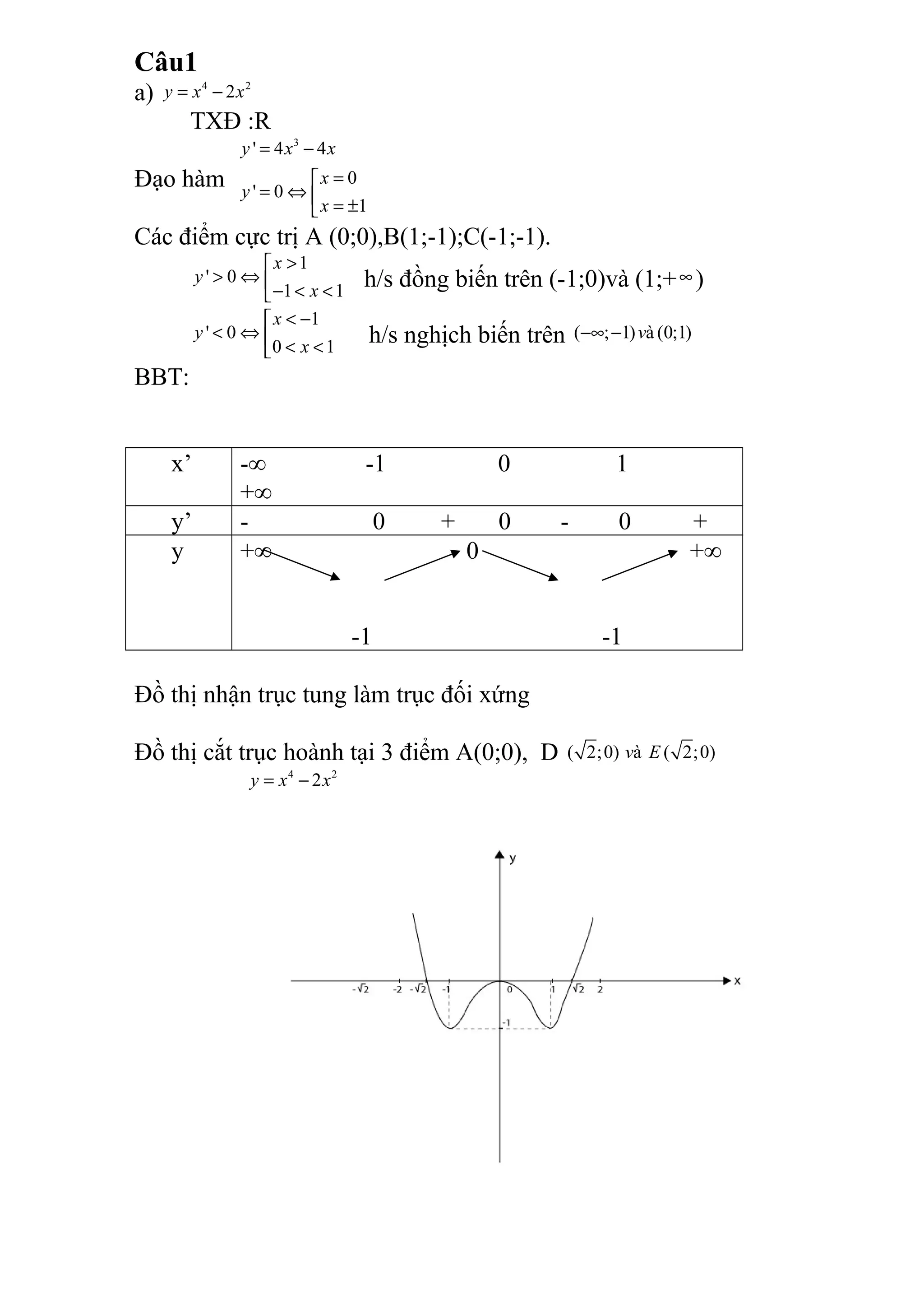
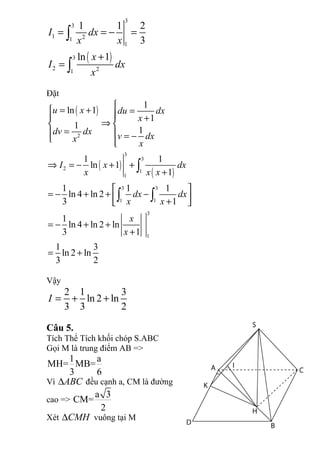
Tài liệu chứa các phép toán và hình học phức tạp, bao gồm việc tìm các cực trị, xác định tính đồng biến và nghịch biến, cũng như giải các phương trình lượng giác. Ngoài ra, tài liệu cũng đề cập đến việc tính thể tích khối chóp và áp dụng các định lý hình học như Pitago. Tổng thể, nội dung chủ yếu tập trung vào việc phân tích và giải quyết các bài toán toán học nâng cao.

1. Câu1
a) 4 2
2y x x= −
TXĐ :R
Đạo hàm
3
' 4 4
0
' 0
1
y x x
x
y
x
= −
=
= ⇔  = ±
Các điểm cực trị A (0;0),B(1;-1);C(-1;-1).
1
' 0
1 1
x
y
x
>
> ⇔ − < <
h/s đồng biến trên (-1;0)và (1;+∞ )
1
' 0
0 1
x
y
x
< −
< ⇔  < <
h/s nghịch biến trên ( ; 1) à (0;1)v−∞ −
BBT:
x’ -∞ -1 0 1
+∞
y’ - 0 + 0 - 0 +
y +∞ 0 +∞
-1 -1
Đồ thị nhận trục tung làm trục đối xứng
Đồ thị cắt trục hoành tại 3 điểm A(0;0), D ( 2;0) à ( 2;0)v E
4 2
2y x x= −

2. b)
( )2 3
3
2
2
4 4 1
' 0 4 4( 1) 0
4 ( 1) 0
0
( 1) 0 (*)
y x m x
y x m x
x x m
x
x m
= − +
= ⇔ − + =
 ⇔ − + = 
=
⇔ 
− + =
Để (1) có 3 cực trị thì pt (*) có 2 nghiệm phân biệt khác 0. ⇔ m+1>0 ⇔ m
>-1
Với m>-1 pt (*) có 2 nghiệm phân biệt
1 1x m= + và 2 1x m= − +
Gọi
2
(0; ); ( 1; 2 1)
( 1; 2 1)
M m N m m
P m m
+ − −
− + − −
Vì đồ thị hàm số đối xứng qua trục 0y nên MNP∆ phải cân tại M
Vậy tam giác MPN vuông tại M suy ra 2 2 2
MN MP NP+ =
3
( 1) ( 1) 1 0m m ⇔ + + − = 
<=>m=0 (vì m>-1)
Vậy m=0
Câu 2.
ĐK: x R∈ ¡

3. ( )
( )
3sin2 cos2 2cos 1
22 3sin cos 2cos 1 2cos 1
cos 3sin cos 1 0
cos 0
3 1 1
sin cos
2 2 2
2
1
sin
6 2
2
2
6 6
5
2
6 6
2
2 , ,
2
2
3
x x x
x x x x
x x x
x
x x
x k
x
x k
x m
x n
x k
x m k n m
x n
π
π
π
π
π
π π
π
π π
π
π
π
π
π
π
+ = −
⇔ + − = −
⇔ + − =
=
⇔
 + =


= +
⇔
  + = ÷  

= +

⇔ + = +


+ = +


= +

⇔ = ∈

= +

¢
Câu 3.
Đặt y = -z
( ) ( )
( )
3 3 2 2
2 2
3 9 22 0
1
2
x z x z x z
x z x z
 + − + − + + =


+ − + =

Đặt

4. ( )
( )
( )
3 2
2
3 2
2
3 3 2 9 22 0
1
2
2
3 3 6 9 22 0 1
1
2 2
2
S SP S P S
S x z
P xz S P S
S SP S P S
S P S
 − − − − + =
= + 
⇒ 
= − − =

 − − + − + =

⇔ 
− − =

Từ (2)
2
2 2 1
4
S S
P
− −
⇒ =
Thay vào (1) ta được :
( ) ( )
( )
3 2 2 2
3 2
2
3 6
2 2 1 3 2 2 1 9 22 0
4 4
2 6 45 82 0
2
2 41 0 3
S S S S S S S S
S S S
S
S S
− − − − + − − − + =
⇔ − + − + =
=
⇔ 
− + =
Phương trình (3) vô nghiệm vì ' 40 0∆ = − <
Vậy
( )
2
3 3 1 1 3
2 ; ; , ;3
4 2 2 2 2
4
x z
S P x z
xz
+ =
    
= ⇒ = ⇒ ⇔ =  ÷  ÷
=    
Vậy ( )
3 1 1 3
; ; , ;
2 2 2 2
x y
   
= − − ÷  ÷
   
Câu 4.
( ) ( )
( )
3 3
2 2 21 1
3 3
1 22 21 1
1 ln 1 ln 11
ln 11
x x
I dx dx
x x x
x
dx dx I I
x x
+ + + 
= = + 
 
+
= + = +
∫ ∫
∫ ∫
Với

5. ( )
3
3
1 21
1
3
2 21
1 1 2
3
ln 1
I dx
x x
x
I dx
x
= = − =
+
=
∫
∫
Đặt
( )
( )
( )
2
3
3
2 1
1
3 3
1 1
3
1
1
ln 1
1
1
1
1 1
ln 1
1
1 1 1
ln 4 ln 2
3 1
1
ln 4 ln 2 ln
3 1
1 3
ln 2 ln
3 2
u x du dx
x
dv dx
v dxx
x
I x dx
x x x
dx dx
x x
x
x

= + =  +
⇒ 
=  = − 
⇒ = − + +
+
 
= − + + − + 
= − + +
+
= +
∫
∫ ∫
Vậy
2 1 3
ln 2 ln
3 3 2
I = + +
Câu 5.
Tích Thể Tích khối chóp S.ABC
Gọi M là trung điểm AB =>
1 a
MH= MB=
3 6
Vì ABC∆ đều cạnh a, CM là đường
cao =>
a 3
CM=
2
Xét CMH∆ vuông tại M

6. Theo Pitago ta có: 2 2 2CH =CM +MH =
2 2a 3 a
+
2 6
   
 ÷  ÷ ÷   
=
7 2a
9
=>
a 7
CH=
3
Ta có ( )( ) · oSC, ABC =SCH=60
· SH a 21
tanSCH= = 3 SH=HC. 3=
HC 3
⇒
=>
2 31 1 a 21 a 3 a 7
V = SH.S = . . =
SABCΔABC3 3 3 4 12
Xét trong mặt phẳng (ABC) kẻ d qua A và song song với BC
Nên BC//(SA;d)
=> [ ] ( )
d =d
BC;SA B SA,d→  
Dựng hình thoi ABCD
Dựng HK
( )
( )
HK AD k AD
HI SK I SK
⊥ ∈
⊥ ∈
Ta có ( )SH ABC SH AD⊥ ⇒ ⊥
Mà HK AD⊥ nên ( )AD SHK⊥
( ) ( )SAD SHK⇒ ⊥
Mà ( )êHI SK n n HI SAD⊥ ⊥
⇒ HI là khoảng cách từ H đến (SAD)
· 2 3
AHsin .
3 2 3
a a
KH KAH= = =
Vì
·
22
2 2 2 2
1 1 1 3 3 24
90 ê
721
7
2 6
o
SHK n n
HI HS HK a aa
a
HI
  
= = + = + = ÷ ÷  ÷   
⇒ =

7. Vì BC//(SAD) và
2
3
HA AB= nên khoảng cách cần tìm là
3 3 7 42
.
2 2 2 6 8
a a
HI = =
Câu 6.
Cách 1:
Không mất tổng quát, giả sử .x y z≥ ≥
Từ giả thiết suy ra ( )z x y= − + do đó,
( )( )
( )( )
22 2
22 2 2 2
3 3 3 12
3 3 3 12
x y y z x z
x y y x x y
P x y x y
x y x y
− − −
− + +
= + + − + + +
= + + − + + +
Đặt
2
2
a x y
b y x
= +

= +
thì
2
3
2
3
a b
x
b a
y
−
=

− =

và 0a b≥ ≥
Thay vào P ta được :
2 2
2 2
3 3 3 2
3 3 3 2 3
2 2
a b a b
a b a b
P a ab b
a b a b
−
−
= + + − − +
+ −   
= + + − + ÷  ÷
   
Đặt ,
2 2
a b a b
u v
+ −
= = thì 0u v≥ ≥ và ta có :
2 2
9 3 3 2 3v u v u v
P u v+ −
= + + − +
Xét hàm:

8. 2 2
2 2
( ) 9 3 3 2 3 , 0
2
'( ) 3 ln3 3 ln3
3
2ln3 2 0
v u v u v
u v u v
P f u u v u v
u
f u
u v
+ −
+ −
= = + + − + ≥ ≥
= + −
+
≥ − >
( )f u⇒ đồng biến trên [ ; )v +∞ kéo theo
2 2
( ) ( ) 9 3 1 2 4
2.9 4 1 (1)
v v
v
f u f v v
v
≥ = + + −
= − +
Xét ( ) 2.9 4 1, 0v
g v v v= − + ≥
'( ) 2.9 ln9 4 4.9 ln3 4 4ln3 4 0 0v v
g v dov= − = − ≥ − > ≥
Suy ra g(v) đồng biến trên [0; ),+∞ kéo theo ( ) (0) 3 (2)g v g≥ =
Từ (1) và (2),suy ra f(u)≥ 3 hay P≥ 3
Đẳng thức xảy ra khi u=v=0 hay x = y = z =0
Vậy min P=3
Cách2
Đặt , ,a x y b y Z c z x= − = − = −
Từ giả thiết suy ra ( )2 2 2
2x y z xy yz zx+ + = − + +
Do đó ( ) ( )2 2 22 2 2
6 2x y z x y y z z x+ + = − + − + −
Vì vậy nếu đặt , ,a x y b y z c z x= − = − = − thì , , 0a b c ≥
và , ,a b c b c a c a b+ ≥ + ≥ + ≥
Ta có
( )2 2 2
3 3 3 2a b c
P a b c= + + − + +
Vì a b c+ ≥ nên ( ) 2
a b c c+ ≥
Tương tự
( )
( )
2
2
b c a a
c a b b
+ ≥
+ ≥
Công ba bất đẳng thức trên ta được
( ) ( ) ( )22 2 2 2 2 2
2 2ab bc ca a b c a b c a b c+ + ≥ + + ⇒ + + ≥ + +
Do vậy

9. ( )
( ) ( ) ( )
3 3 3
3 3 3
a b c
a b c
P a b c
a b c
≥ + + − + +
= − + − + −
Xét hàm
( )
( )
( ) ( )
'
3 , 0
3 ln3 1 0
0 1
x
x
f x x x
f x
f x f
= − ≥
= − >
⇒ ≥ =
Vì Vậy 3P ≥ , dấu “=” xảy ra khi x = y = z = 0
Câu 7.
a).
( )
( )
22
1
11 3
15 3 52
,
22 52 1
h d M AN
− −
= = = =
+ −
Đặt
6 , 0AB x x= >
Có
2
2
2
2 2 2 2 2
1 1
. 6 .2 6
2 2
1 1
. 6 .3 9
2 2
1 1
. 3 .4 6
2 2
36 6 9 6 15
ADN
ABM
CMN
AMN ABCD ADN ABM CMN
S AD DN x x x
S AB BM x x x
S CM CN x x x
S S S S S
x x x x x
= = =
= = =
= = =
⇒ = − − −
= − − − =

10. Theo định lý pitago 2 2
AN AD DN= +
2 2
2
36 4 2 10
2 30 15 3 5 1
22 10 10 2
AMN
x x x
S x x
h x
AN x
= + =
⇒ = = = ⇒ ⇒ =
Định lý pitago
2 2 2 2 45
36 9 145
2
AM AB BM x x x= + = + = =
:2 3 0 2 3AN x y y x− − = ⇔ = −
Đặt: ( ;2 3)A a a −
2 2
2 2
2 2
11 1 45
2 3
2 2 2
11 7 45
2
2 2 2
5 25 20 0 5 4 0
1
4
a a
a a
a a a a
a
a
   
⇒ − + − − = ÷  ÷
   
   
⇔ − + − = ÷  ÷
   
⇔ − + = ⇔ − + =
=
⇔  =
Vậy 1 2(1; 1), (4;5)A A−
Câu 8.
a).
Gọi
( )
( )
( 1;2 ; 2)
1;2 ; 2
0;0;3
A a a a
B b b b
I
− +
− + Với a ≠ b

11. ( )
( )
( )
( )
22 2 2
22 2 2
1;2; 1
1;2 ; 1
2 1 4 6 4 2
2 1 4 6 4 2
IA a a
IB b b b
IA a a a a
IB b b b b
→
→
⇒ = − −
= − −
⇒ = − + = − +
= − + = − +
Vì IAB∆ Vuông cân tại I nên
( ) ( )
( )
( ) ( )
2 22 2
2 1 1 4 0. 0
6 4 2 6 4 2
3 1 0 (1)
6 4 0 (2)
a b abIA IB
a a b bIA IB
ab a b
a b a b
→ →
  − − + = =
⇔ 
− + = − += 
− + + =
⇔ 
− + − =   
Từ (2) vì a ≠ b
2
3
a b⇔ + = thế vào (1)
Ta được
1
9
ab = −
2
1 2
3
1 2
3
8
3
a
b
IA
 +
=

⇒ 
− =
⇒ =
Vậy
( ) ( )
22 2 8
: 3
3
S x y Z+ + − =
Câu 9.
a).

12. ( ) ( )
1 3
2
2
5
1 2
5
1.2.3
30 3 2
3 28 0
7( / )
4( )
n
n
nC C
n n n
n
n n
n n
n t m
n loai
−
=
− −
⇔ =
⇔ = − +
⇔ − − =
=
⇔ =−
Khai triển
7 72 2
7 1 1
14 2
x x
hay
x x
   
− − ÷  ÷
   
Số hạng tổng quát là
( )7
72
7
14 3
7
1
2
1 . , , 7
2
k k
k
k
kk
k
x
C
x
x
C k N k
−
−
−
   
− ÷  ÷
  
= − ∈ ≤
Xét
14 3 5 3k k− = ⇔ =
Vậy số hạng chứa 5
x là
( )
5
33 5
7 4
35
1
2 16
x
C x− = −
Câu 7b) Do tính đối xứng của (E) nên giao điểm của (C) và (E) là đỉnh
hình vuông thỏa mãn A(a;a) a>0
Suy ra 2 2
8 2a a a+ = ⇒ =
2 2
2 2 2 2
4 4
( ): 1 1
x y
E
m n m n
+ = ⇒ + =
Vì 2m=8 nên m=4
2
2
1 4 16
1
4 3
n
n
⇒ + = ⇒ =

13. Vậy
2 2
( ): 1
1616
3
x y
E + =
Câu 8b) Viết lại (d) dưới dạng:
2 1
( )
2
x t
y t t
z t
= −

= ∈
 = +
¡
Giả sử M(2t-1;t;t+2) N (a;b;c)
Ta có
2 1 2 3 2
2 2
2 4 2
2 5 0 2 5 0
3 2 2 4 2 5 0
2
t a a t
t b b t
t c c t
a b c a b c
t t t
t
− + = = − 
 + = − = − − 
⇔ 
+ + = = − 
 + − + = + − + = 
⇒ − − − − + + =
⇔ =
Vậy M(3;2;4), khác A => thỏa mãn
Câu 9 b)
Đặt
( ), .Z a bi a b R= + ∈
( ) ( ) ( )
( ) ( )
5
2
2 1
5 2 1
5 5 5 2 2 2
3 2 6 7 0
3 2 0 1
6 7 0 1
Z i
i
a bi i i a bi
a bi i a bi ai b i
a b i b a
a b a
b a b
−
 
+ ÷
  = −
+
⇔ − + = − + +
⇔ − + = + + − + −
⇔ − − + − + =
− − = = 
⇔ ⇔ 
− + = = 
Vậy
( )
22
2 2
1 , 1 1 2 1 2
W=1+1+i+2i=2+3i
2 3 13
Z i Z i i i
Z
= + = + = + − =
⇒
= + =