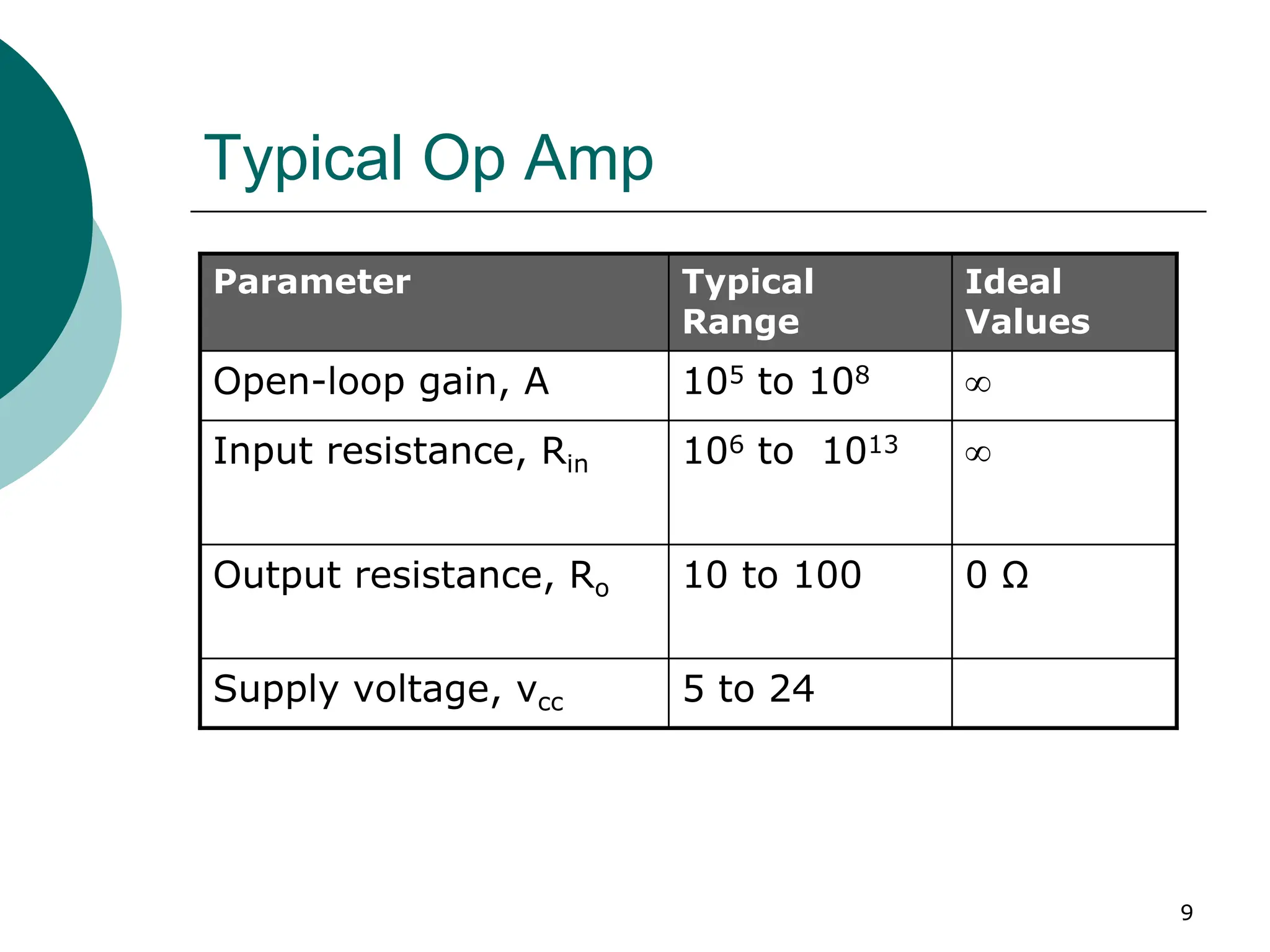
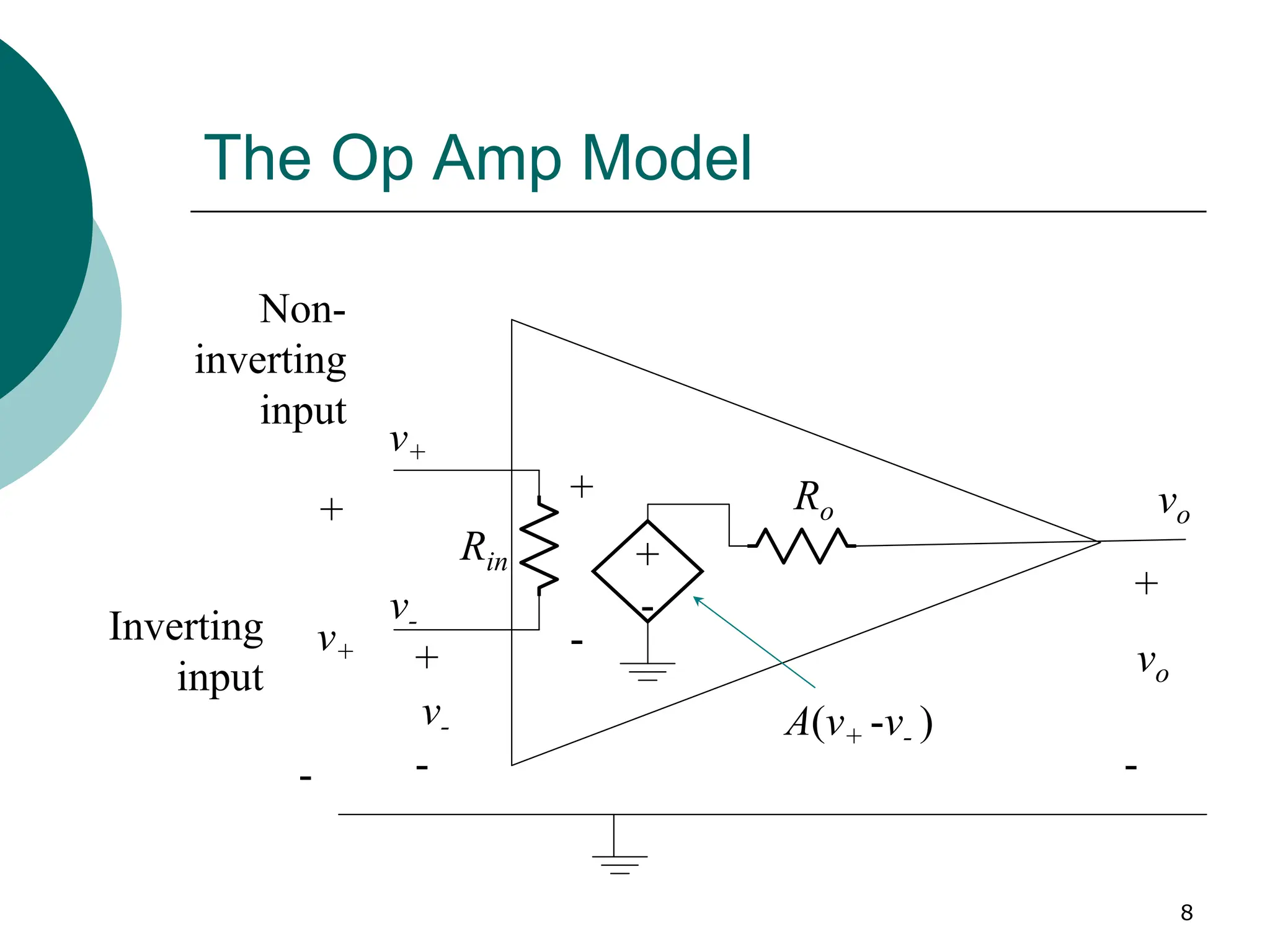
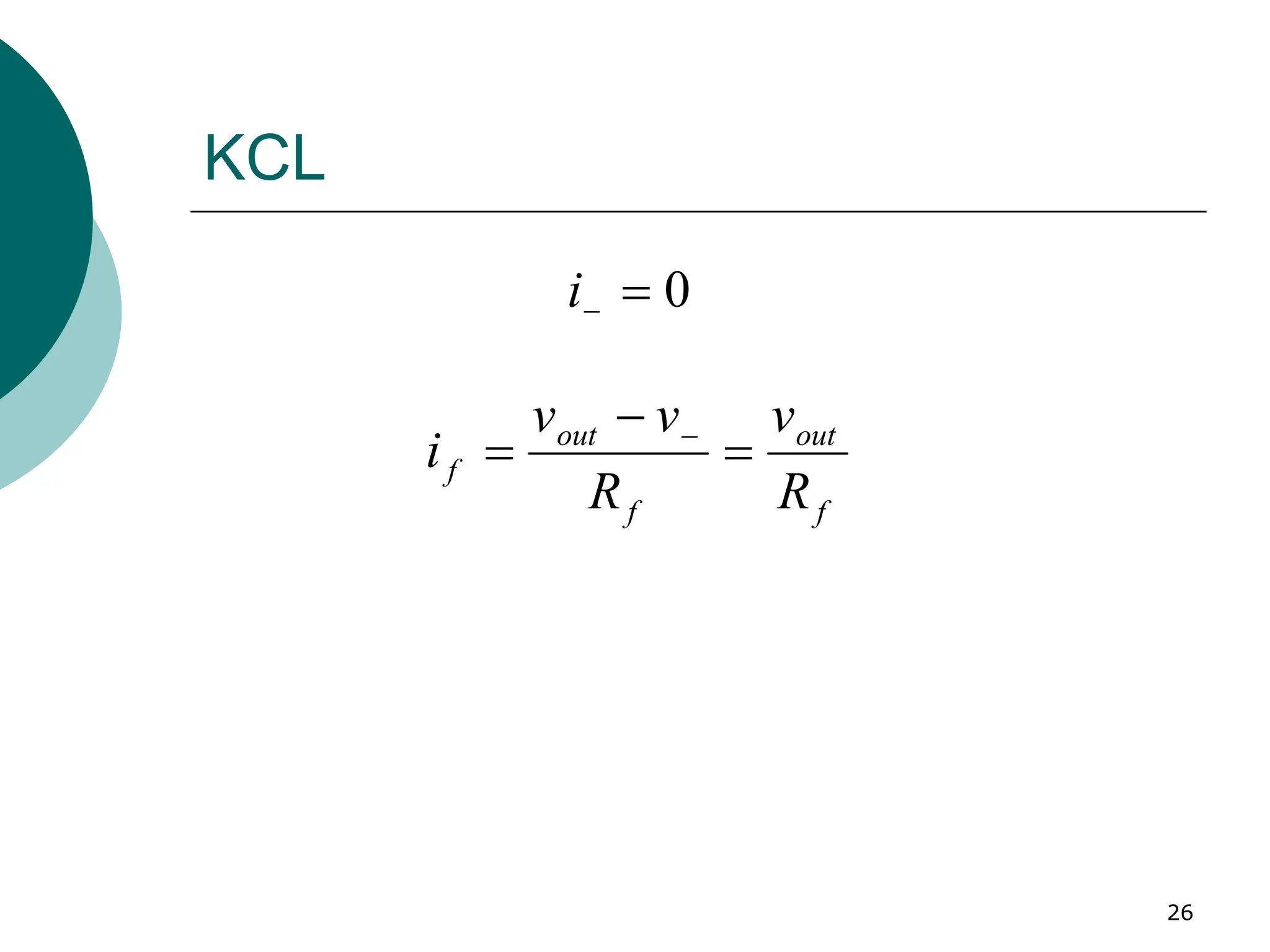
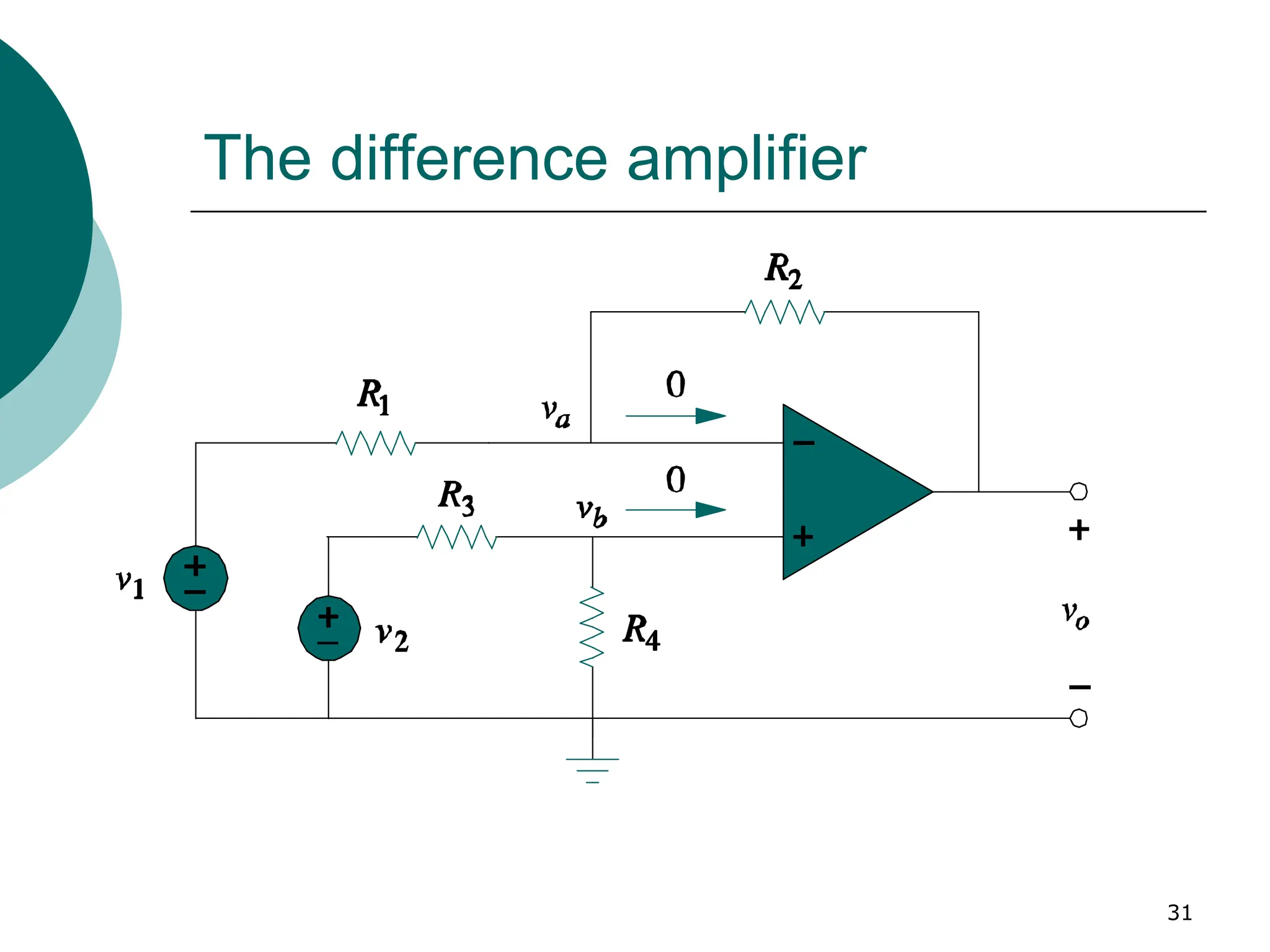
ideal op amp Properties of an ideal op amp: 1. No currents enters the input terminals: i1 = i2 = 0 2. Zero ohms output resistance: Rout = 0 3. The op amp only responds to the difference between its two input voltages, i.e., Vo = Aod(V2 – V1 ) 4. The gain of the op amp is infinite, i.e., Aod = ∞ Signal amplitude ≈ 1 mV • Noise level will be significant • will need to amplify and filter • We’ll use filtering ideas from the last two lectures

1. 1
Operational Amplifiers
(Op Amps)
Dr. Mustafa Kemal Uyguroğlu

2. 2
Introduction
{ Op Amp is short for operational
amplifier.
{ An operational amplifier is modeled
as a voltage controlled voltage
source.
{ An operational amplifier has a very
high input impedance and a very
high gain.

3. 3
Use of Op Amps
{ Op amps can be configured in many
different ways using resistors and
other components.
{ Most configurations use feedback.

4. 4
Applications of Op Amps
{ Amplifiers provide gains in voltage
or current.
{ Op amps can convert current to
voltage.
{ Op amps can provide a buffer
between two circuits.
{ Op amps can be used to implement
integrators and differentiators.

5. 5
More Applications
{ Lowpass and bandpass filters.

6. 6
The Op Amp Symbol

7. 7
Schematic diagram of op amp

8. 8
The Op Amp Model
+
-
Inverting
input
Non-
inverting
input
Rin
v+
v-
+
-
A(v+ -v- )
vo
Ro
+
-
v-
+
+
-
-
v+ vo

9. 9
Typical Op Amp
5 to 24
Supply voltage, vcc
0 Ω
10 to 100
Output resistance, Ro
∞
106 to 1013
Input resistance, Rin
∞
105 to 108
Open-loop gain, A
Ideal
Values
Typical
Range
Parameter

10. 10
Example
{ A 741 op amp has an open-loop voltage gain of 2 x 105, input
resistance of 2 MΩ, and output resistance of 50 Ω.The op amp is
used in the circuit shown below. Find the closed- loop gain v0/vs. Find i0
when vs = 1 V.
+
-
5 kΩ
vs
40 kΩ
io
20 kΩ vo
+
-
+
-
+
-
vs
2 MΩvin 2 ×10
5
vin
50 Ω io
40 kΩ
5 kΩ 20 kΩ vo
Equivalent circuit

11. 11
Example cont.
io
+
-
+
-
vs
2 MΩ
vin
5 kΩ
v1
40 kΩ
2 ×10
5
vin
50 Ω
vo
20 kΩ
1 1 0
1
6 3 3
0
2 10 5 10 40 10
s
v v v v
v
− −
+ + =
× × ×
•Redrawn for clarity
KCL at v1
KCL at v0
5
0 0 1 0 1
3 3
2 10 ( )
0
20 10 40 10 50
s
v v v v v v
− − × −
+ + =
× ×
v0 = 9.0004vs
i0 = 0.675 mA

12. 12
“Ideal” Op Amp
{ The input resistance is infinite,
Rin=∞
{ The gain is infinite, A = ∞
{ Zero output resistance, Ro= 0
{ The op amp is in a negative
feedback configuration.

13. 13
Consequences of the Ideal
{ Infinite input resistance means the
current into the inverting input is
zero:
i- = 0 = i+
{ Infinite gain means the difference
between v+ and v- is zero:
v+ - v- = 0

14. 14
Example
vo
io
+
-
i- = 0
i+ = 0
vs
vs
vs
40 kΩ
5 kΩ 20 kΩ
vo
0
0
0
40 5
9
s s
s
v v v
v v
−
+ =
=
KCL at noninverting
terminal:
If vs = 1 V then i0 = 0.65 mA
0 0
0
20 40
s
v v v
i
k k
−
 
= +
 
 
KCL at v0:

15. 15
Inverting Amplifier
1 2 0
v v
= =
0
1 2
1
0 0
i
f
v v
i i
R R
− −
= ⇒ =
Since the noninverting terminal is grounded
KCL at v1:
0
1
f
i
R
v v
R
= −

16. 16
Where is the Feedback?
-
+
Vin
+
-
+
-
Vout
R1
R2

17. 17
Review
{ To solve an op amp circuit, we
usually apply KCL at one or both of
the inputs.
{ We then invoke the consequences
of the ideal model.
i- = 0 = i+
v+ - v- = 0
{ We solve for the op amp output
voltage.

18. 18
The Non-Inverting Amplifier
+
-
vin
+
-
+
-
vout
R1
R2

19. 19
KCL at the Inverting Input
+
-
vin
+
-
+
-
vout
R1
R2
i-
i1 i2

20. 20
KCL
0
=
−
i
1
1
1
R
v
R
v
i in
−
=
−
= −
2
2
2
R
v
v
R
v
v
i in
out
out −
=
−
= −
Since v- = v+ = vin

21. 21
Solve for Vout
0
2
1
=
−
+
−
R
v
v
R
v in
out
in








+
=
1
2
1
R
R
v
v in
out

22. 22
The Voltage Follower

23. 23
Inverting Summer
_ = 0

24. 24
KCL at the Inverting Input
-
+
v2
+
-
+
-
vout
R2
Rf
R1
v1
+
-
i1
i3
if
i-
v3
+
-
R3
i2

25. 25
KCL
since 0
v− =
1
1
1
1
1
R
v
R
v
v
i =
−
= −
2
2
2
2
2
R
v
R
v
v
i =
−
= −
3 3
3
3 3
v v v
i
R R
−
−
= =

26. 26
KCL
0
=
−
i
f
out
f
out
f
R
v
R
v
v
i =
−
= −

27. 27
Solve for Vout
3
1 2
1 2 3
0
out
f
v v
v v
R R R R
+ + + =
1 2 3
1 2 3
f f f
out
R R R
v v v v
R R R
= − − −

28. 28
Noninverting Summer
+
-
v2
+
-
+
-
vout
R2
Ra
R1
v1
+
-
i1
i3
ia
i-
v3
+
-
R3
i2
Rf
if

29. 29
1 2 3
1
1
1
0
i i i
v v
i
R
+
+ + =
−
=
2
2
2
v v
i
R
+
−
=
3
3
3
v v
i
R
+
−
=
KCL at noninverting input: KCL at inverting input:
0
f a
out
f
f
i i
v v
i
R
−
+ =
−
=
a
a
a
out
a f
v
i
R
R
v v
R R
v v
−
−
− +
=
=
+
=

30. 30
1 2 3
3
1 2
1 2 3 1 2 3
1 2 3
3
1 2
1 2 3
0
1 1 1
1 1 1 1
1
T
a
out
T a f
i i i
v
v v
v
R R R R R R
R R R R
v R
v v
v
R R R R R R
+
+ + =
 
+ + = + +
 
 
 
= + +
 
 
+ + =
+
1 2 3
1 2 3
1
f T T T
out
a
R R R R
v v v v
R R R R
  
= + + +
  
  

31. 31
The difference amplifier

32. 32
2
3 4
4
2
3 4
KCL at node :
b
b b
b a
v
v v v
R R
R
v v v
R R
−
=
= =
+

33. 33
1
1 2
1
2 1 2 1
2 2 2 4 2
1 2 1
1 1 1 3 4 1
1
2
2 2 2 2
0 2 1 2 1
3 3
1 1 1 1
4 4
KCL at
0
1 1 1 1
1 1
1
1
1
1 1
a
a a o
o a
o a
v
v v v v
R R
v v v
R R R R
R R R R R
v v v v v
R R R R R R
R
R
R R R R
v v v v v
R R
R R R R
R R
− −
+ =
 
= + −
 
 
   
= + − = + −
   
+
   
 
+
 
   
= + − = −
 
  + +

34. 34
{ Since a difference must reject a signal common
to the two inputs, the amplifier must have the
property that v0 = 0 when v1 = v2. This implies
that
4
3
2
1
R
R
R
R
=
When R1 = R2 and R3 = R4 it acts like a subtractor
1
2 v
v
vo −
=

35. 35
Interconnecting of Op Amps

36. 36
Example
+
+
+
- - -
v1 v2
v3
10 kΩ
10 kΩ
40 kΩ
20 kΩ
20 kΩ
50 kΩ
25 kΩ
25 kΩ
12 V
Find the voltage transfer equation of the following circuit