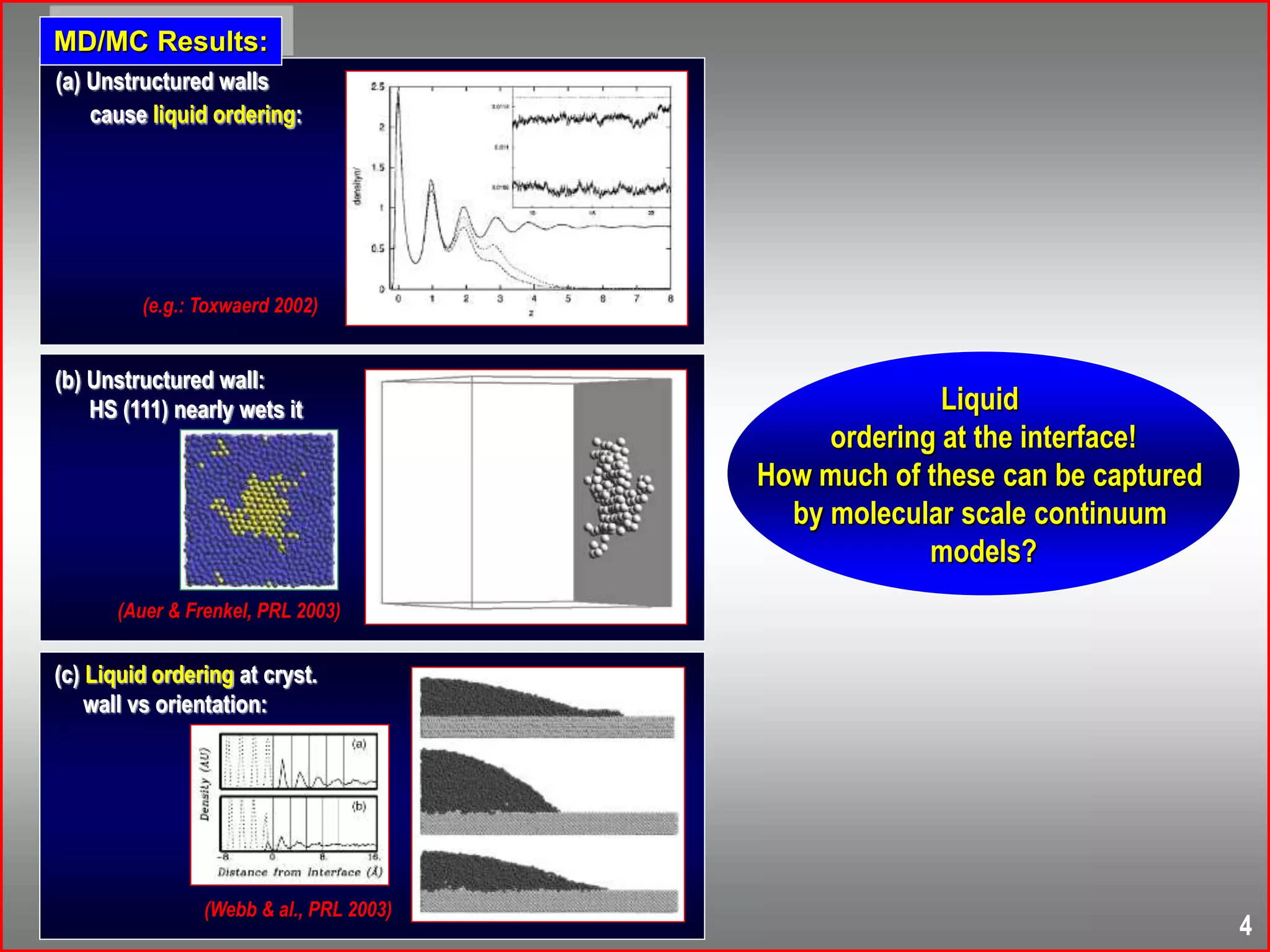
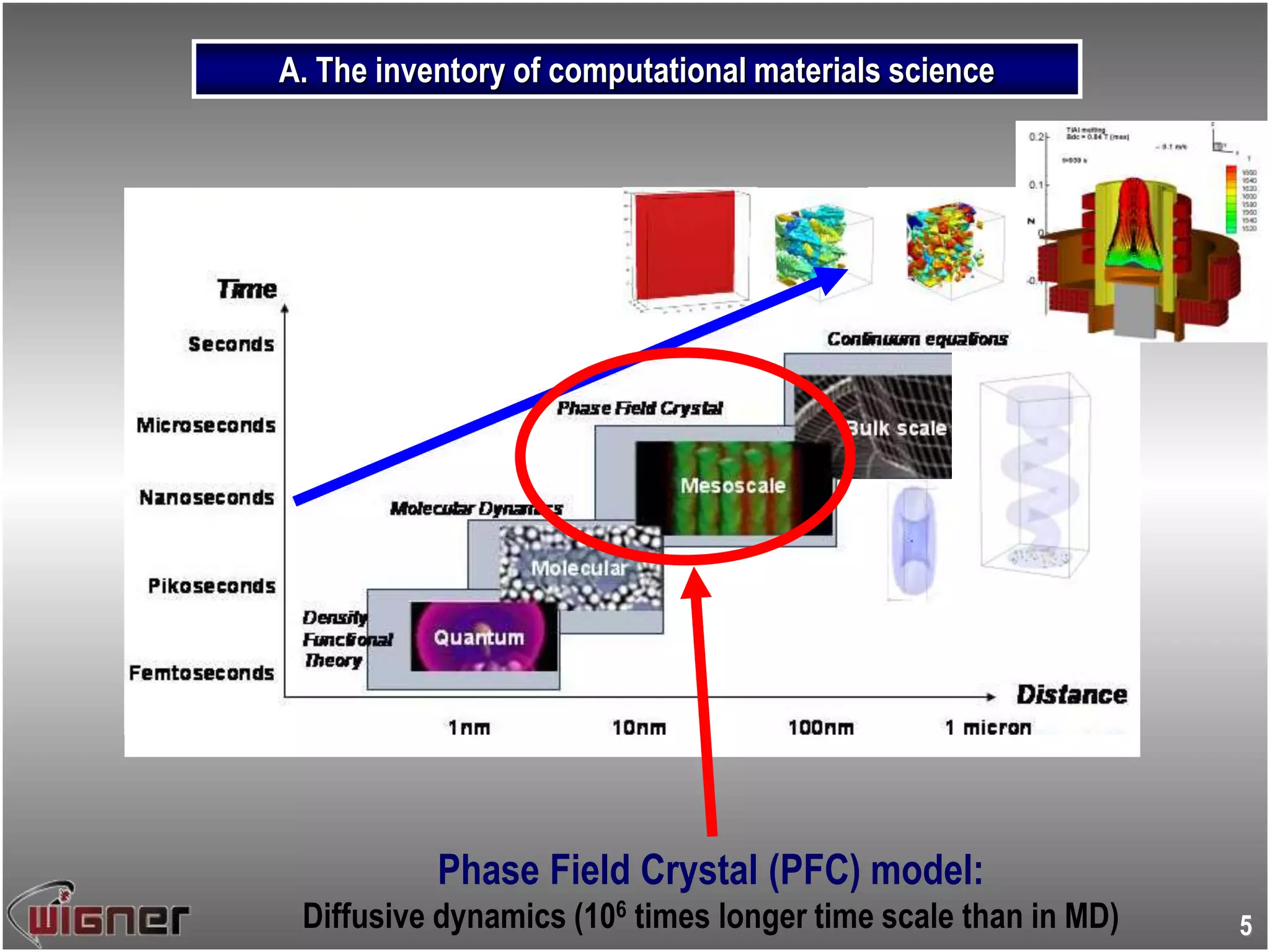
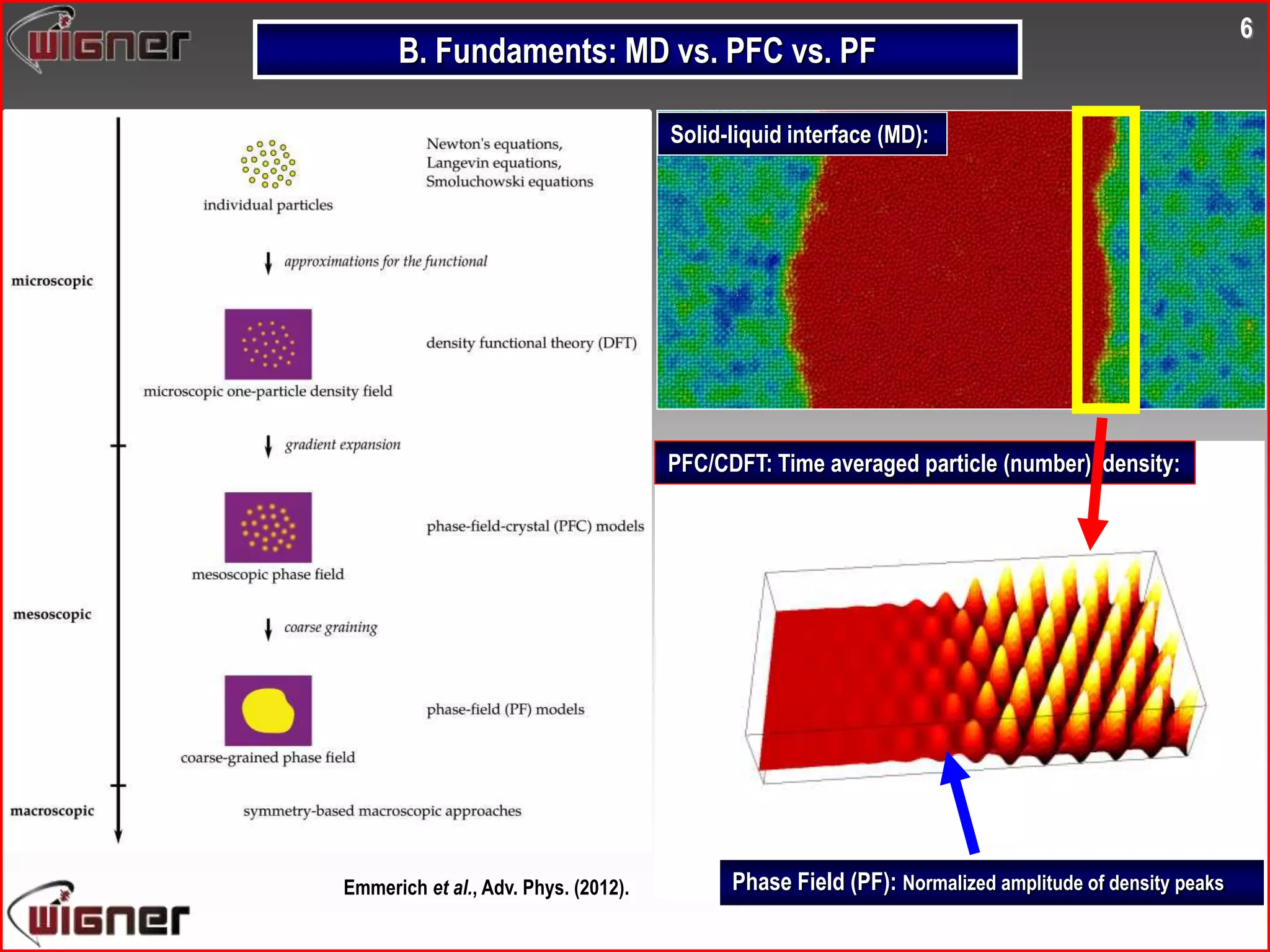
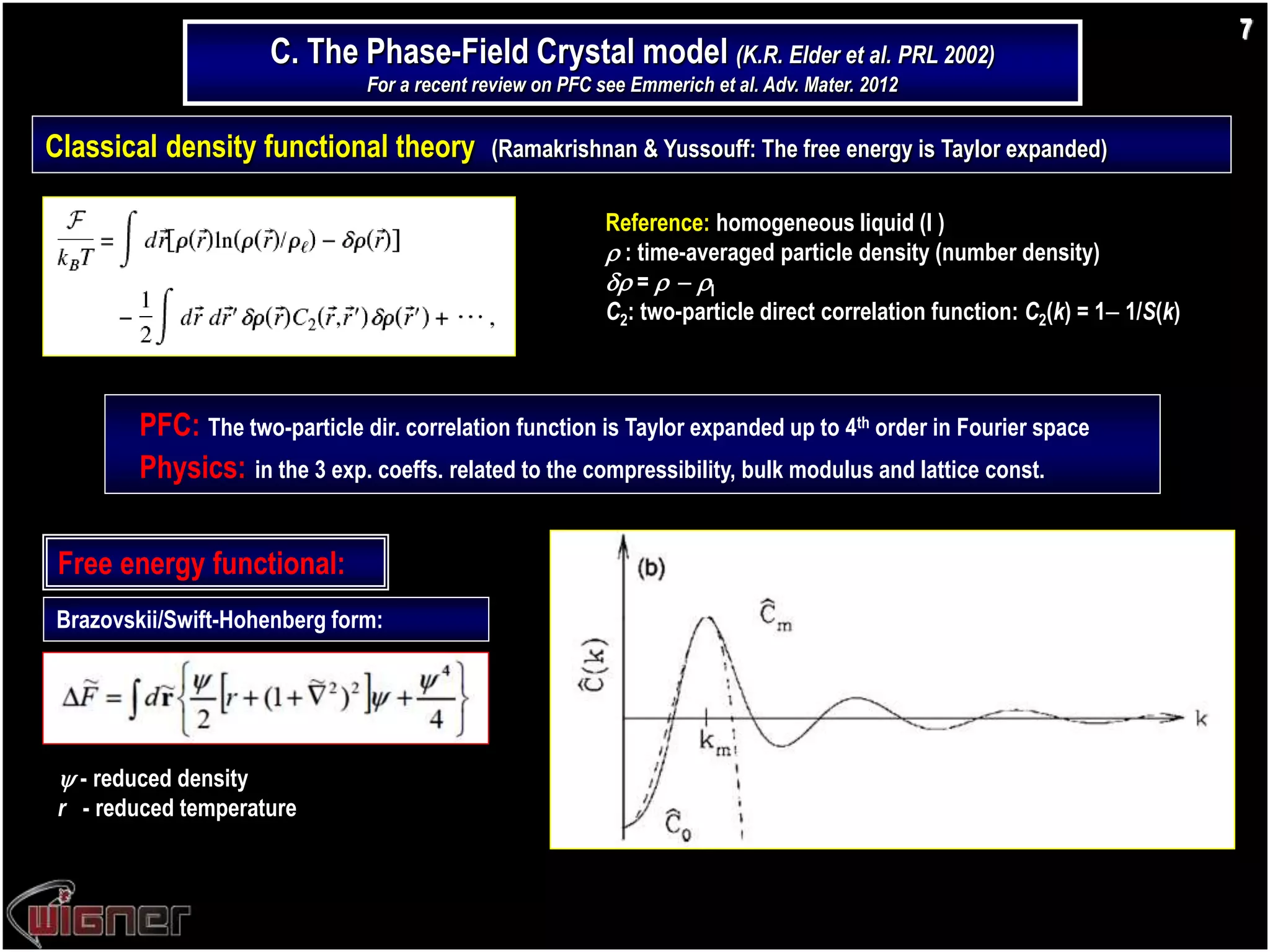
This document summarizes research on modeling nucleation processes using phase-field crystal modeling. It begins with an introduction to complex polycrystalline structures that form through nucleation and growth processes. It then provides an overview of the phase-field crystal approach and how it can be used to model nucleation and growth dynamics. Specific applications discussed include modeling homogeneous and heterogeneous nucleation barriers using the Euler-Lagrange method and simulating non-equilibrium nucleation processes using the diffusive phase-field crystal model. The document highlights how phase-field crystal modeling can provide insights into precursor structures, growth morphologies, and freezing mechanisms observed in experiments.

1. Nucleation III:
Phase-field crystal modeling of nucleation processes
aWigner Research Centre for Physics, H-1525 Budapest, P. O. Box 49, Hungary
bBCAST, Brunel University, Uxbridge, Middlesex UB8 3PH, U.K.
L. Gránásy,a,b
Phase Field Workshop “Focus on Nucleation”,
27 Sep 2018, Center for Hierarchical Materials Design HQ, Northwestern
University, Evanston, IL, USA

2. Complex patterns evolve
due to the interplay of
nucleation and growth.
I. Introduction
1American Pale Ale Dirty Martini Vodka Tonic
Gin
Water Polycrystalline matter: Atmospheric sciences:
- technical alloys - aerosol formation (climate change)
- ceramics
- polymers
- minerals
- food products, etc.
In biology:
- bones, teeth
- kidney stone
- cholesterol in arteries
- amyloid plaques in Alzheimer’s disease
Also frozen drinks:
A. Complex polycrystalline structures:

3. B. Stages of polycrystalline freezing:
Nucleation, growth, and grain coarsening
2
1. Nucleation: ~ 10 nm 2. Growth: 10 nm – mm
Interface controlled: v  1/ e.g., pure metals
Diffusion controlled: v  t -1/2 e.g., colloids
3. Grain coarsening:
10 nm – mm

4. (a) BCC layer appears at the
FCC-L interface:
Crystalline precursor!
MD/MC for LJ:
(ten Wolde et al. PRL 1995)
(cf.: Alexander & McTague, PRL 1978)
Precursors everywhere!
Nucleation can be
fairly complex even in
simple systems …
MD/MC Results:
DFT for LJ:
(Lutsko & Nicolis, PRL 2006)
(c) Amorphous precursor
MC for hard-spheres:
(Schilling et al., PRL 2010)
BD for hard-spheres:
(Kawasaki & Tanaka, PNAS 2010)
(c) Medium Range Crystalline Order
Liquid precursor!
Atomistic simulations:
(ten Wolde & Frenkel, Science 1997)
(b) Two-step nucleation (near MS Tc)
(a) Non-spherical nuclei:
(~ HS colloids)
Laser Scan. Conf. Microscopy:
(Gasser et al. Science 2001)
Experiment:
AFM:
(Vekilov et al., Nature 2000)
(b) Chain-like nuclei (apoferritin)
(c) Amorphous precursor
Microscopy:
(Zhang & Li., JACS 2007)
3

5. Liquid
ordering at the interface!
How much of these can be captured
by molecular scale continuum
models?
(b) Unstructured wall:
HS (111) nearly wets it
(Auer & Frenkel, PRL 2003)
(a) Unstructured walls
cause liquid ordering:
(e.g.: Toxwaerd 2002)
(Webb & al., PRL 2003)
(c) Liquid ordering at cryst.
wall vs orientation:
MD/MC Results:
4

6. II. The Phase-Field Crystal Approach:
Fundamentals

7. Phase Field Crystal (PFC) model:
Diffusive dynamics (106 times longer time scale than in MD)
A. The inventory of computational materials science
5

8. B. Fundaments: MD vs. PFC vs. PF
6
Solid-liquid interface (MD):
Phase Field (PF): Normalized amplitude of density peaks
PFC/CDFT: Time averaged particle (number) density:
Emmerich et al., Adv. Phys. (2012).

9. Classical density functional theory (Ramakrishnan & Yussouff: The free energy is Taylor expanded)
PFC: The two-particle dir. correlation function is Taylor expanded up to 4th order in Fourier space
Physics: in the 3 exp. coeffs. related to the compressibility, bulk modulus and lattice const.
Reference: homogeneous liquid (l )
 : time-averaged particle density (number density)
 =   l
C2: two-particle direct correlation function: C2(k) = 1 1/S(k)
Free energy functional:
Brazovskii/Swift-Hohenberg form:
7
C. The Phase-Field Crystal model (K.R. Elder et al. PRL 2002)
For a recent review on PFC see Emmerich et al. Adv. Mater. 2012
 - reduced density
r - reduced temperature

10. C. Nucleation barrier in 2D:
D. 3D dendrite
B. Nucleation & growth as in colloids
DPFC
Tegze et al. Soft Matter 2011
Experiment
I. Diffusive PFC (DPFC):
Equation of motion (EOM):
diffusive dynamics – colloids
Time evolution:
8
C. DPFC: growth modes as in colloids
Euler-Lagrange eq. (ELE):
(extremes of free energy)
Equilibrium properties:
- phase diagram
- interface free energy & anisotropy
- nucleation barrier, etc.
DPFC
A. Crystal-liquid interface
Experiment
B. Equilibrium shapes: Parameter r regulates anisotropy.
A. Phase diagrams in (a) 2D and (b) 3D:
Podmaniczky et al.,
J. Cryst. Growth (2014)

11. III. The Phase-Field Crystal (PFC) Approach:
Nucleation and the Euler-Lagrange/
elastic band/string methods
- Homogeneous nucleation
- Heterogeneous nucleation (contact angles, barriers, corners)
- Free growth limited version of particle-induced nucleation

12. Solution of EL eq.: by pseudo-spectral iteration method
Initial guess: single-mode solution for r < R (R varied)
Large no. of solutions
r =  0.5
CNT:
Hexagonal shape
(Ecorner neglected)
Sharp interface
Driving force known
Parabolic fit to find max.

A. Homogeneous crystal nuclei in 2D (ELE) Tóth et al. J. Phys: Condens. Matter, 2010
11

13. Results:
Comparable nucleation barriers for BCC & FCC
 BCC  FCC
(far from critical point  large Sf  faceted)
BCC FCC
Homogeneous crystal nuclei in 3D (ELE) Tóth et al. J. Phys: Condens. Matter, 2010
12

14. Results:
- Adsorbed monolayer !
- Contact angle: 60 , determined by crystal structure
r =  0.5
a0/ = 1.0
V term added
to F
B. Heterogeneous crystal nuclei in 2D (ELE) Tóth et al. J. Phys: Condens. Matter, 2010
13
  )(),()(:Potential 10 rrr haSVVV s

15. Nearly isotropic ( = 0.25) ; 0 =  0.341, V0 = V1 = 0.5 Faceted ( = 0. 5) ; 0 =  0.51415, V0 = 0, V1 = 0.65
Contact angle () and barrier height (W*)
are nonmonotonic functions of as
  )(),()(:Potential 10 rrr haSVVV s
Effect of lattice mismatch in 2D (ELE) Tóth et al. Phys. Rev. Lett., 2012
14

16. r =  0.25
EL solutions for increasing driving force:
Homogeneous nuclei at
the critical driving force
r =  0.5
C. Particle-induced crystallization in 2D (ELE) Tóth et al. Phys. Rev. Lett., 2012
15

17. r =  0.25
256  256  256 grid
SC substrate
Cubic shape
512  512  512 grid
Particle-induced crystallization in 3D (ELE) Tóth et al. Phys. Rev. Lett., 2012
16

18. Nuclei for homogeneous process:
D. Homogeneous/heterogeneous nucleation in 2D by simplified string method
Backofen et al., J. Phys.: Condens. Matter, 2010; and Eur. Phys. J. Special Topics, 2014
17
Nucleus for heterogeneous process:
Finding the minimum energy path (MEP):
String: ordered set of states & its length
Evolution step:
Reparametrization step:
Repeat the two steps until MEP is found.

19. IV. The Phase-Field Crystal Approach:
Dynamic Equations and Simulating Nucleation
- DPFC: PFC with diffusive dynamics: K. R. Elder et al., PRL, 2002

20. 1. “Single-mode” 1M-PFC
by Elder et al.:
R1 = relative strength of 1st and 2nd mode contributions
Q1 = q1 / q0 (= 2/3 for fcc) ratio of the two wave-numbers
2. “Two-mode” 2M-PFC
by Wu et al.:
Unified: where R1 =  / (1  )
 = 1 1M-PFC
 = 0 2M-PFC
18
Free energy functionals of advanced PFC models:
Phase diagrams in 3D: 1M-PFC 2M-PFC

21. 3. “Multi-mode” MM-PFC
by Mkhonta et al. (PRL 2013):
19
Further advanced PFC models:
4. “Eight-order fitting PFC” EOF-PFC
by Jaatinen et al. (PRB 2009):
c2 is expanded at km up to 8th order
Parameters are fixed so as to recover position, height &
c2”at 1st peak
Phase diagrams in 3D: 3M-PFC EOF-PFC
Tang et al. PRE 2017

22. Two-step homogeneous nucleation
DPFC: G. I. Tóth et al., PRL, 2011
HPFC: F. Podmaniczky, preliminary

23. Continuous cooling in DPFC: Berry et al., PRE (2008).
20
- At fast cooling amorphous phase forms via 1st
order phase transition
- At large undercoolings the nucleation barrier
for the amorphous phase is smaller than for BCC

24. Continuous cooling: from r =  0.1330 to  0.1875; cooling time: 3104, 105, 2  105, 3  105 time steps
21

25. Zhang & Liu, JACS (2007)
r =  0.1684
0 = 0.25
256256256 grid
req =  0.1330
Tóth et al. PRL (2011).
Red (bcc-like) if
q4  [0.02, 0.07]
q6  [0.48, 0.52]
Steinhardt, Nelson, Ronchetti, PRB (1983)
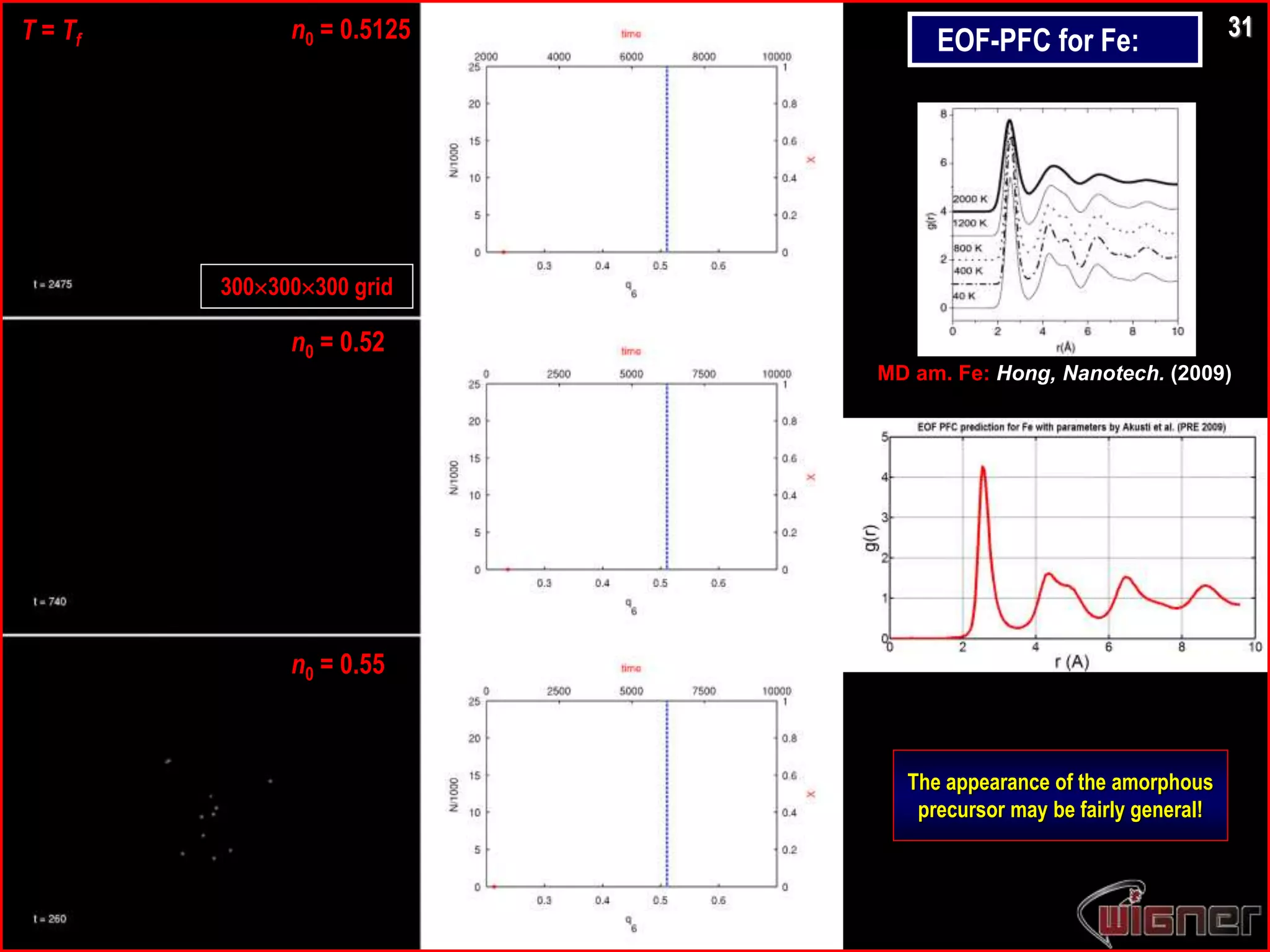
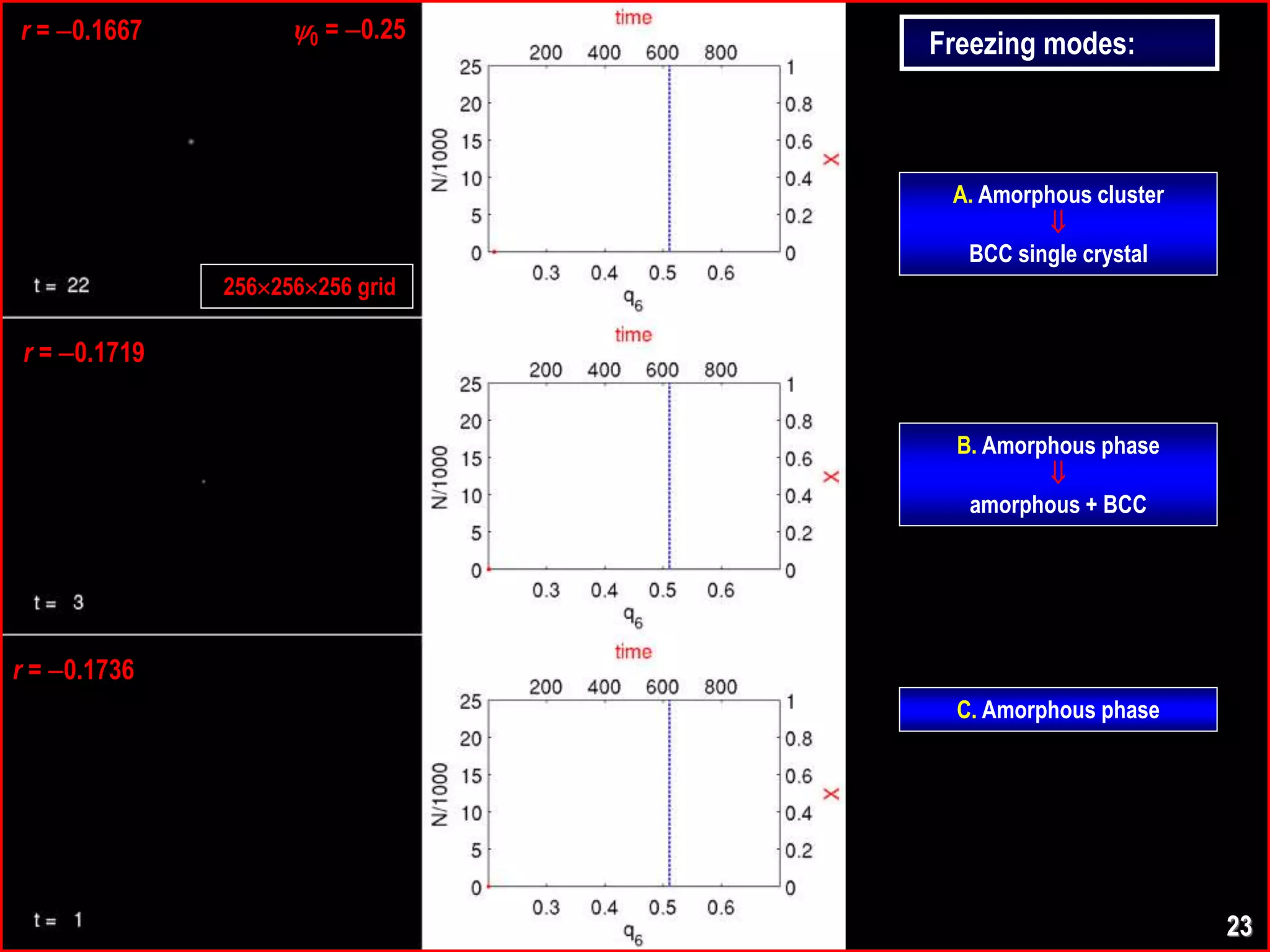
Starts to solidify as amorphous,
then crystallizes ! A’la 2D & 3D colloids.
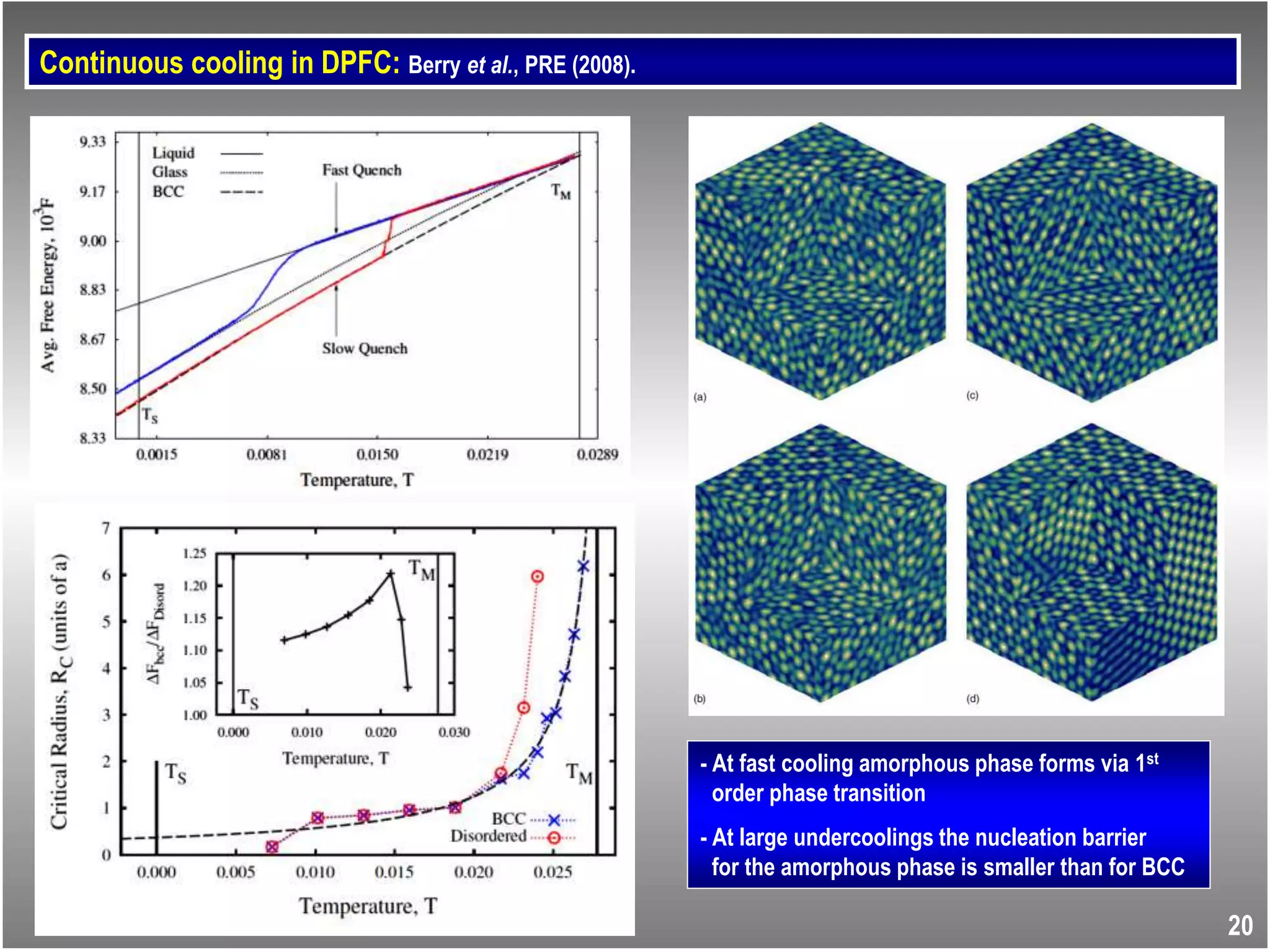
Instantaneous quench in DPFC: 22

26. r = 0.1667
r = 0.1719
r = 0.1736
256256256 grid
A. Amorphous cluster

BCC single crystal
B. Amorphous phase

amorphous + BCC
C. Amorphous phase
0 = 0.25
Freezing modes:
23

27. Lechner & Dellago, JCP (2008)
qi of Lechner & Dellago
Black: bcc
Yellow: Icosah.
Green: hcp
Red: fcc
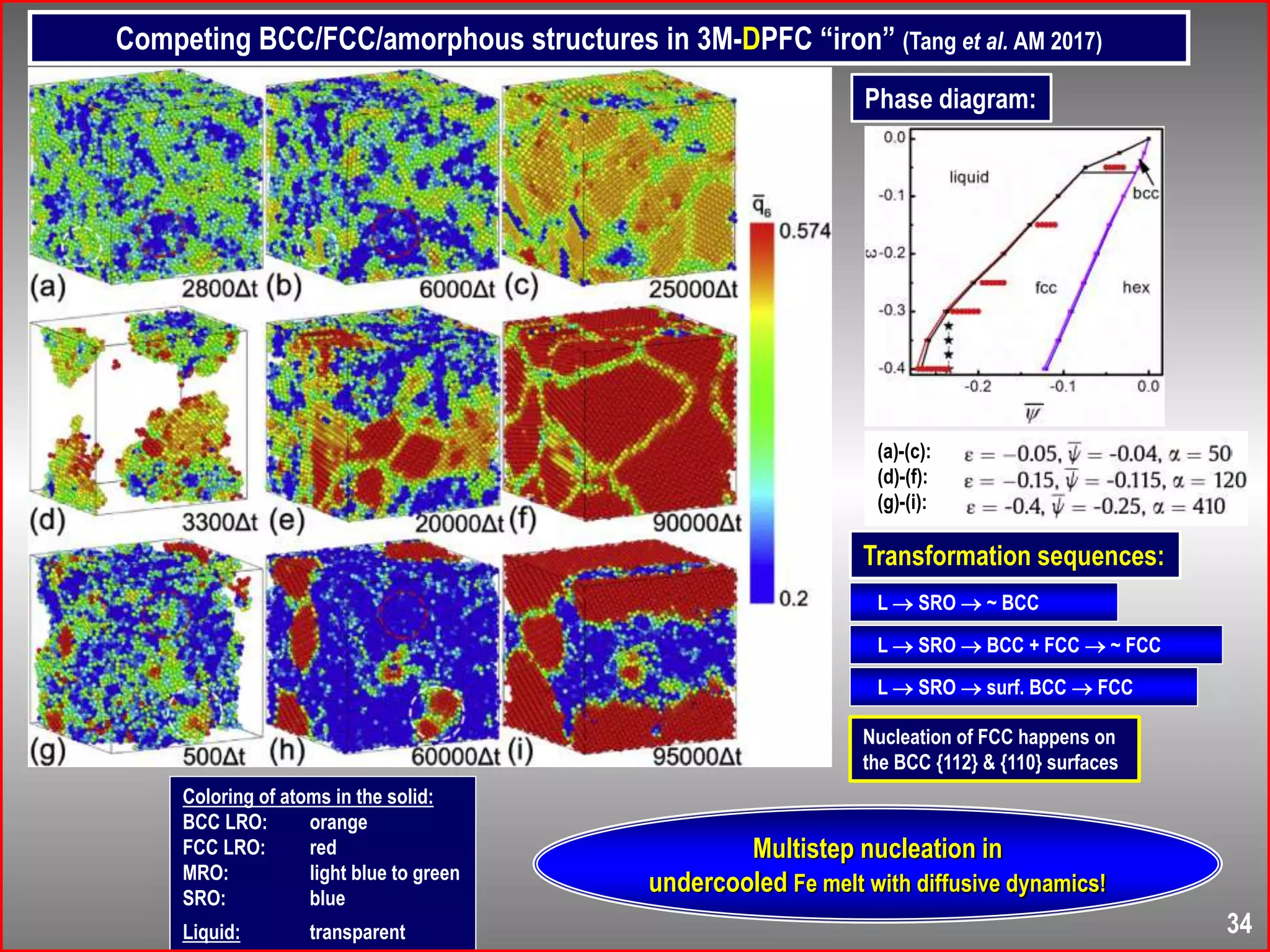
Structural aspects:
Greenq6 > 0.4
Redq6 [0.28, 0.4]
Whiteq6 < 0.28
Red (bcc-like) if
q4  [0.02, 0.07]
q6  [0.48, 0.52]
Observations:
- Am. precursor is structurally like LJ liquid
- MRCO and amorphous domains appear parallel
- Heterogeneous-like bcc nucleation on am. domains
- Literature: LJ, HS, colloids, now PFC. What else?
Kawasaki & Tanaka, PNAS (2010)
MRCO (Brownian Dynamics)
24

28. Model: 1M-PFC
am
Nucleation maps:
25

29. Model: 2M-PFC
26

30. Nucleation with noise:
(under the conditions we used)
- An amorphous precursor precedes bcc nucleation.
- Practical observation: We cannot nucleate other
crystalline phase than bcc !!!
- Amorphous phase appears to help bcc nucleation.
- Amorphous phase coexists with the liquid & nucleates!!!
SUBSTANTIAL DIFFERENCE IN DENSITY?
Transition between 1M-PFC and 2M-PFC ( varies, 0 = 0.25):
27

31. (MS) liq  amo(S) liq  fcc
The density
difference between
liq. and am. phases
is comparable to
the difference
between liq. and
fcc.
(MS) amo  fcc
(1) EOM: We do not see (noise-induced) solidification for  <  0.2
(2) EL: From the evaluated data Wamo < Wfcc for  >  0.217; consistent with EOM
(3) FCC nucleation should be seen for  <  0.217; but accessible time is too short
Eq. (ELE)
amo-l=1.7910-4
fcc-l =2.7610-4
Wam < Wfcc 
 >  0.217
Thermodynamics for 2M-PFC at r = 0.1 (from solving the ELE):
28

32. 0 = 0.21775
Eq. (ELE)
amo-l=1.7910-4
fcc-l =2.7610-4
Wam < Wfcc 
 >  0.217
Direct fcc nucleation from the melt?
Yes!
Just we cannot see it in EOM
simulations due to technical reasons.
29

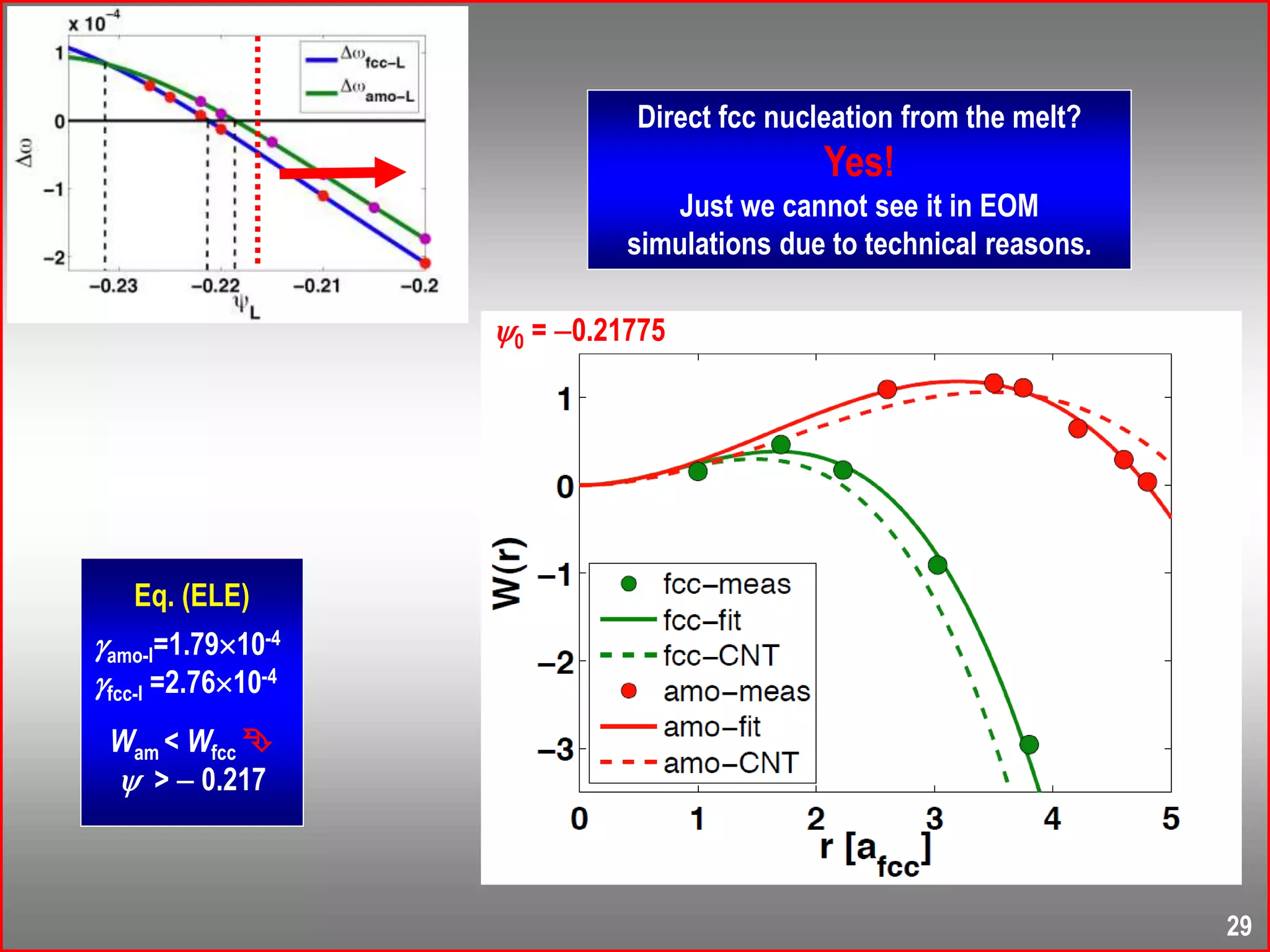
33. Potential from g(r):
Schommers’ iterative method
- initial guess (potential of mean force)
- MC 4096 particle  g(r)
correction to u(r):
f kT log[gPFC(r)/gsim(r)]
(repeat these steps until convergence)
(Efficient and accurate for one component
fluids, Schommers PRA 1983)
Work done with Gergely Tóth,
Eötvös University, Inst. of Chemistry
Budapest, Hungary
Amorphous structure & eff. pair potential vs. :
PFC models:
Molecular Dynamics:
Am. Fe: Hong,
Nanotech. (2009)
Am. Ni: Yu et al.,
TNMSC (2006)
Like Dzugutov’s potential for
monatomic model glass former:
Peak at ~ 2 rmin
(suppresses fcc, hcp & sc crystals)
Why amorphous precursor?
30
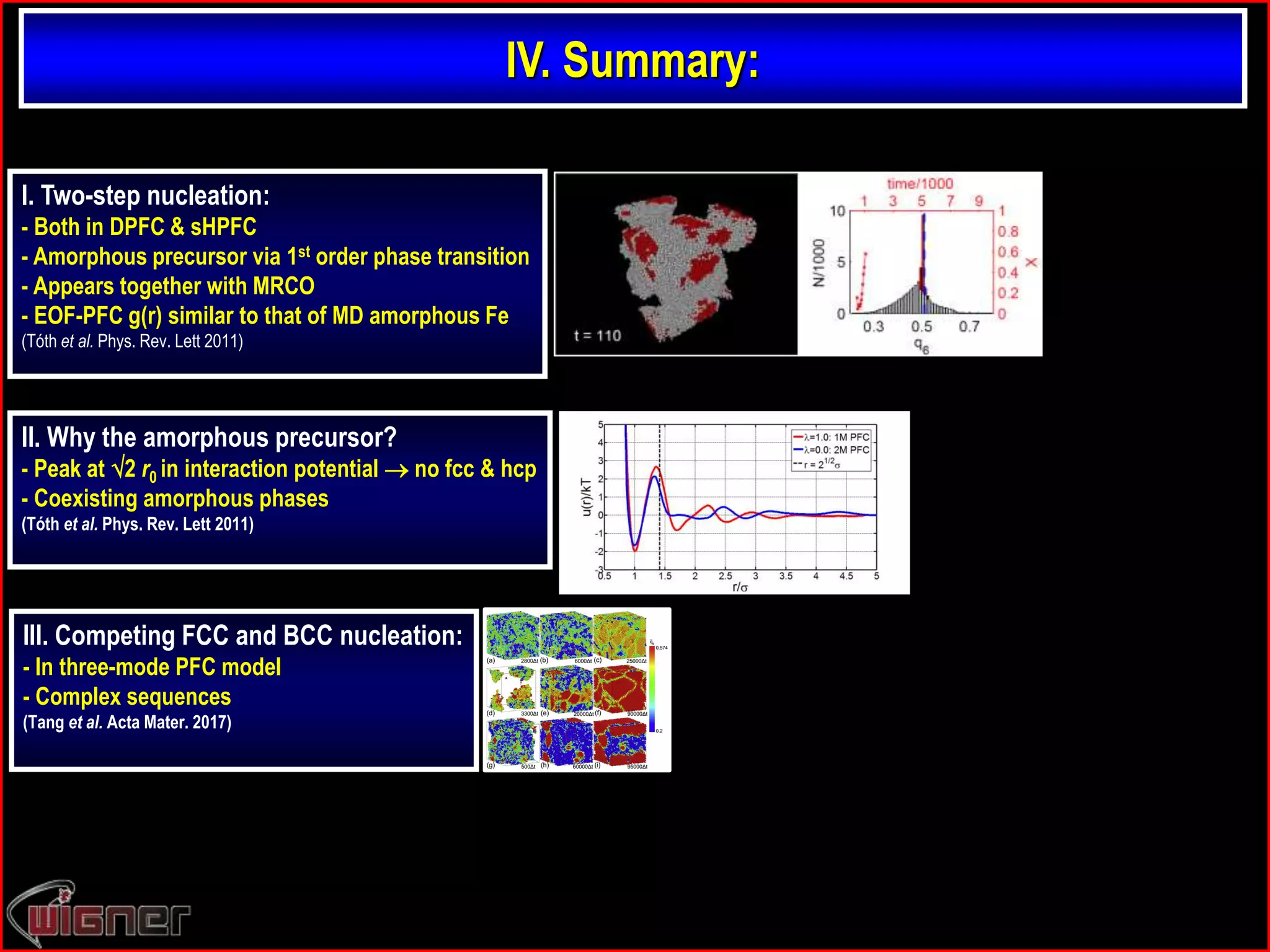
Summarizing the results for LJ, HS, & PFC potentials:
(see Tóth at al. PRL 2011)
- Repulsive core suffices for an amorphous precursor;
- Peak at ~ 2 rmin appears to suppress fcc & hcp;
- Multiple minima  coexisting disordered phases;
(a’la Mishima & Stanley, Nature 1998)

34. T = Tf
300300300 grid
n0 = 0.5125
n0 = 0.52
n0 = 0.55
MD am. Fe: Hong, Nanotech. (2009)
The appearance of the amorphous
precursor may be fairly general!
31
EOF-PFC for Fe:

35. Multistep nucleation in
undercooled Fe melt with diffusive dynamics!
34
Competing BCC/FCC/amorphous structures in 3M-DPFC “iron” (Tang et al. AM 2017)
(a)-(c):
(d)-(f):
(g)-(i):
Coloring of atoms in the solid:
BCC LRO: orange
FCC LRO: red
MRO: light blue to green
SRO: blue
Liquid: transparent
L  SRO  ~ BCC
L  SRO  BCC + FCC  ~ FCC
L  SRO  surf. BCC  FCC
Nucleation of FCC happens on
the BCC {112} & {110} surfaces
Phase diagram:
Transformation sequences:

36. 23p
IV. Summary:
I. Two-step nucleation:
- Both in DPFC & sHPFC
- Amorphous precursor via 1st order phase transition
- Appears together with MRCO
- EOF-PFC g(r) similar to that of MD amorphous Fe
(Tóth et al. Phys. Rev. Lett 2011)
III. Competing FCC and BCC nucleation:
- In three-mode PFC model
- Complex sequences
(Tang et al. Acta Mater. 2017)
II. Why the amorphous precursor?
- Peak at 2 r0 in interaction potential  no fcc & hcp
- Coexisting amorphous phases
(Tóth et al. Phys. Rev. Lett 2011)