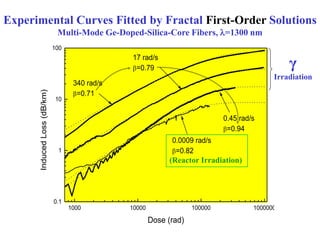
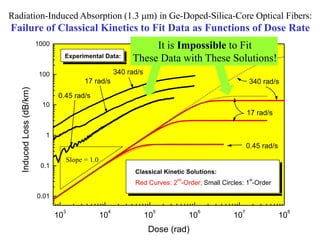
This document summarizes the key findings from fitting experimental data on radiation-induced absorption in optical fibers to fractal kinetic models. The models provide better fits than classical kinetic solutions, with fitting parameters suggesting a transition from classical to fractal behavior at lower dose rates. Specifically: 1) Fractal kinetic models with stretched exponential solutions provided excellent fits to the data over four orders of magnitude in dose rate. 2) Parameters like the rate coefficient and saturation value varied with dose rate as predicted by the fractal models, indicating a transition from classical to fractal kinetics. 3) Including additional defect populations improved fits and supported the fractal kinetics interpretation of the data.

1. David L. Griscom
impactGlass research international
Mexico City Paris Tokyo Washington
Commissariat à l’Energie Atomique, Bruyères-le-Châtel, France
1 December 2005

2. An
Ideal Wedding
of a Mathematical Formalism
often written off as “just another method of curve fitting”
with a Remarkable Body of Data
which has defied simple mathematical description,
thus severely limiting its utility for its intended purposes

3. Acknowledgements
The Experimental data for the Ge-doped-silica fibers were
recorded at the Naval Research Laboratory by E.J. Friebele
with important assistance from M.E. Gingerich, M. Putnum,
G.M. Williams, and W.D. Mack.
A full account of this work has been published:
D.L. Griscom, Phys. Rev. B64, 174201 (2001)

4. Classical Kinetic Solutions for Radiolytic Defect Creation with
Thermal Decay: Dependencies on Dose Rate
10
3
10
4
10
5
10
6
10
7
10
8
0.01
0.1
1
10
100
1000
Classical Kinetic Solutions:
Red Curves: 2
nd
-Order; Small Circles: 1
st
-Order
340 rad/s
17 rad/s
0.45 rad/s
Experimental Data:
17 rad/s
0.45 rad/s
340 rad/s
InducedLoss(dB/km)
Dose (rad)
Slope = 1.0

5. Radiation-Induced Absorption (1.3 m) in Ge-Doped-Silica-Core Optical Fibers:
Failure of Classical Kinetics to Fit Data as Functions of Dose Rate
10
3
10
4
10
5
10
6
10
7
10
8
0.01
0.1
1
10
100
1000
Classical Kinetic Solutions:
Red Curves: 2
nd
-Order; Small Circles: 1
st
-Order
340 rad/s
17 rad/s
0.45 rad/s
Experimental Data:
17 rad/s
0.45 rad/s
340 rad/s
InducedLoss(dB/km)
Dose (rad)
Slope = 1.0
It is Impossible to Fit
These Data with These Solutions!

6. •Gottfried von Leibnitz (1695): “Thus it follows that d½x will be equal to xdx:x,
… from which one day useful consequences will be drawn.”
What is Fractal (Fractional) Kinetics?
•I.M. Sokovov, J. Klafter, A. Blumen, Physics Today, November, 2002, p. 48:
“Equations built on fractional derivatives describe the anomalously slow diffusion
observed in systems with a broad distribution of relaxation times.”
•R. Kopelman, Science 241, 1620 (1988).
•Science 297, 1268 (2002): News article on “Tsallis entropy”.
(q  1)

7. Fractal Kinetics in Brief
Fractal spaces differ from Euclidian spaces by having fractal dimensions df
such that
df < d,
where d is the dimension of the Euclidian space in which the fractal is embedded.
Each fractal also possesses a spectral dimension ds (< df < d), defined by the
probability P of a random walker returning to its point of origin after a time t:
P(t)  t-ds/2.
The present work introduces a parameter, ds/2. Thus, for many amorphous
materials, values of 2/3 might be expected ...
– which
serves as a prototype for many amorphous materials.
It is known that ds  4/3 for the entire class of random fractals embedded in
Euclidian spaces of dimensions d  2 , including the percolation cluster

8. Supercomputer Simulations of Fractal Kinetics
Raoul Kopelman, Science 241, 1620 (1988)
A + B  AB
Sierpinski “gasket”: df =1.585, ds = 1.365 Percolation Cluster: df =1.896, ds = 1.333

9. First-order growth kinetics with thermally activated decay.
The classical rate equation for this situation can be written
dN(t)/dt = KDN* - RN,
and its solution is given by
N(t) = Nsat{1 - exp[-Rt]},
where K and R are constants, D is the dose rate, N* is a
number of unit value and dimensions of number density
(e.g., cm-3), and
Nsat = (KD/R)N*.
Rate Equations for Defect Creation under Irradiation
•
•
•

10. Result of Change in Dimensionless Variable kt  (kt)
First-order growth kinetics with thermally activated decay.
The fractal rate equation for this situation can be written
dN((kt))/d(kt) = (KD/R) N* - N
0 <  <1 k = R
with solution
N((kt)) = Nsat{1 - exp[-(kt)]},
where Nsat = (KD/R) N*.
•
•

11. Second-order growth kinetics with thermally activated decay.
The classical rate equation for this situation can be written
dN(t)/dt = KDN* - RN2/N*,
and its solution is given by
N(t) = Nsattanh(kt),
where Nsat = (KD/R)1/2N* and k = (KDR)1/2.
Rate Equations for Defect Creation under Irradiation
•
• •

12. Result of Change in Dimensionless Variable kt  (kt)
Second-order growth kinetics with thermally activated decay.
The fractal rate equation for this situation can be written
dN((kt))/d(kt) = (KD/R) /2N* - (R/KD) /2N2/N*
0 <  <1 k = (KDR)1/2
with solution
N((kt)) = Nsattanh[(kt)],
where Nsat = (KD/R) /2N*.
•
••
•
Three Fitting
Parameters

13. Experimental Curves Fitted by Fractal First-Order Solutions
Multi-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
1000 10000 100000 1000000
0.1
1
10
100
0.0009 rad/s
=0.82
17 rad/s
=0.79
0.45 rad/s
=0.94
340 rad/s
=0.71
InducedLoss(dB/km)
Dose (rad)
(Reactor Irradiation)
γ
Irradiation

14. 1E-3 0.01 0.1 1 10 100
10
100
(c)
Slope = 
Slope = /2
SaturationLoss(dB/km)
Dose Rate (rad/s)
1E-3 0.01 0.1 1 10 100
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
Linear!!!
(b)
Classical 1st-Order Kinetics
Classical 2nd-Order
Kinetics
RateCoefficient(s
-1
)
1E-3 0.01 0.1 1 10 100
0.7
0.8
0.9
(a)
Stretched 2nd Order Kinetics
Stretched 1st-Order Kinetics
Power-LawExponent
Fractal-Kinetic Fitting Parameters: Both Kinetic Orders
Multi-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Slope = 1
Classical 1st Order
Classical 2nd
Order Fractal 1st & 2nd Order (Slope = 1) Empirical!!!
Fractal 1st & 2nd Order
(Slope Variable)
Annoying Cusp
Annoying

k
Nsat
Dose Rate (rad/s)
Classical 1st Order
Slope = ½
Classical 2nd Order

15. 1000 10000 100000 1000000
0.1
1
10
100
0.0009 rad/s
=1.0
17 rad/s
=0.70
0.45 rad/s
=1.00
340 rad/s
=0.62
InducedLoss(dB/km)
Dose (rad)
Experimental Curves Fitted by Fractal Solutions (Second Order)
Multi-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
“Population B” Included in Fits
Population B (included in all four curve fits)
Dose-Rate-Independent
N.B. The dominant “Population A” comprises
all defects with thermally activated decays

16. Fractal-Kinetic Fitting Parameters (Second Order)
Multi-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Parameters for
dose-rate-
independent
“Population B”
included in fits
for all four dose
rates
1E-3 0.01 0.1 1 10 100
1
10
100
(c)
Slope = 
Slope = /2
SaturationLoss(dB/km)
Dose Rate (rad/s)
1E-3 0.01 0.1 1 10 100
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
Linear
(b)
RateCoefficient(s
-1
)
1E-3 0.01 0.1 1 10 100
0.6
0.7
0.8
0.9
1.0
(a)
Power-LawExponent
No More
Annoying Cusp
Here!
Approximately
Straight Line Here
Intended Result of
Introducing
“Population B”:
Rate Coefficient
Is More Perfectly
Linear than Before!!!

k
Nsat
Dose Rate (rad/s)
Slope=/2
Empirical!!!
Happy Colateral
Consequences:

17. Fractal-Kinetic Fitting Parameters (Second Order)
Multi-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Proposed
“Canonical Form”
for
Classical  Fractal
Phase Transition
1E-3 0.01 0.1 1 10 100
1
10
100
Slope = 1/2
(c)
Slope = /2
SaturationLoss(dB/km)
Dose Rate (rad/s)
1E-3 0.01 0.1 1 10 100
10
-7
10
-6
10
-5
10
-4
10
-3
Slope = 1/2
(b)
Slope = 1
RateCoefficient(s
-1
)
1E-3 0.01 0.1 1 10 100
0.6
0.7
0.8
0.9
1.0
(a)
Classical Fractal
Power-LawExponent
Here “Population B”
was contrived to give
classical behavior
below the point where
 = 1

k
Nsat
Slope=/2
Slope=1
Slope=1/2
Slope=1/2
Classical Fractal
Dose Rate (rad/s)

18. 1000 10000 100000 1000000
0.1
1
10
100
C ( = 0.66)
B
0.0009 rad/s
=1.0
17 rad/s
=0.61
0.45 rad/s
=0.94
340 rad/s
=0.46
InducedLoss(dB/km)
Dose (rad)
Experimental Curves Fitted by Fractal Solutions (Second Order)
Single-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Dose-Rate-Independent “Populations B and C” Included in Fits
(Reactor Irradiation)
Populations B and C

19. 1E-3 0.01 0.1 1 10 100
0.1
1
10
Slope = 1/2
Slope = /2(c)
SaturationLoss(dB/km)
Dose Rate (rad/s)
1E-3 0.01 0.1 1 10 100
1E-8
1E-7
1E-6
1E-5
1E-4
1E-3
Slope = 1/2
Slope = 1(b)
RateCoefficient(1/s)
1E-3 0.01 0.1 1 10 100
0.5
0.6
0.7
0.8
0.9
1.0
Single-Population Fits
Fits Including Effects
of Populations B & C(a)
Exponent
Fractal-Kinetic Fitting Parameters (Second Order)
Single-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
However…
All fits are constrained
by the (questionable)
assumption that the
dosimetry for reactor-
irradiation is equivalent
to that for γ irradiation
vis-à-vis the induced
optical absorption.
γ-Rays
Reactor
Irradiation Dose Rate (rad/s)

k
Nsat
Slope=1/2
Slope=1/2
Inclusion of Populations
B & C does not alter the
fundamental result:
There still seems to be a
classical  fractal
transition.

20. Experimental Curves Fitted by Fractal Solutions (Second Order)
Single-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Dose-Rate-Independent “Populations B and C” Included in Fits
1000 10000 100000 1000000
0.1
1
10
100
C
B
0.011 rad/s
=1.017 rad/s
=0.66
0.45 rad/s
=0.85
340 rad/s
=0.52
InducedLoss(dB/km)
Dose (rad)
( Irradiation)

21. Fractal-Kinetic Fitting Parameters (Second Order)
Single-Mode Ge-Doped-Silica-Core Fibers, =1300 nm
Now All Fits
Pertain to
γ-Irradiated
Fibers Only.
Classical  Fractal Transition
0.01 0.1 1 10 100
1
10
Slope = /2
(c)
SaturationLoss(dB/km)
Dose Rate (rad/s)
0.01 0.1 1 10 100
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
Slope = 1
(b)
RateCoefficient(1/s)
0.01 0.1 1 10 100
0.5
0.6
0.7
0.8
0.9
1.0
Fits Including Influences
of Populations B and C
Single-Population Fits
(a)
Exponent
No Data for Reactor-
Irradiated Fibers Are
Included.
Empirical Result
of Fractal Kinetics!
Slope=1
Slope=/2
Dose Rate (rad/s)

k
Nsat
But Caution:
 May Now Be
Asymptotic to 1.0
as the Dose Rate
Approaches Zero.
?
?

22. Fractal Kinetics of Defect Creation in Ge-Doped-Silica Glasses:
What Have We Learned by Simulation of the Growth Curves?
==========================================================
Parameters
__________________________________________________
First-Order Solution Second-Order Solution
==========================================================
Specified by k = R k = (KDR)½
New Formalisms
Nsat = (KD/R) Nsat = (KD/R) /2
______________________________________________________________
Empirically R  D R  D1/2
Inferred in This Work
K  D½ K  D1/2
==========================================================
Note:
In classical cases
(=1), both K and
R are constants.
In fractal cases
(0<<1), both K
and R are dose-
rate dependent.
•
••
• •
••
Empirically

23. Post-Irradiation Thermal Decay Curves and Fractal-Kinetic Fits
for γ-Irradiated Ge-Doped-Silica Core Fibers
1 10 100 1000 10000 100000 1000000
0
10
20
30
40
50
60
70
80
90
SM Fiber Data
MM Fiber Data
Naive Fractal Second-Order
Prediction from Growth-Curve Fit
(=0.62)
Fractal Second-Order
Best Fit (=0.51)
Fractal 1
st
-Order
Best Fit
(=0.44)
Fractal Secnd-Order
Best Fit (=0.54)
Naive Fractal
First-Order
Prediction from
Growth-Curve Fit
(=0.71)
InducedLoss(dB/km)
Time (s)
Non-Decaying Component
Fractal Second-Order
Best Fit (=0.54)
Fractal Second-Order
Best Fit (=0.51)
(Equal to
Cumulative
Populations
B and C
Used in
Fitting the
Growth
Curves!)

24. 10
1
10
2
10
3
10
4
10
5
10
6
Time (s)
 = 0.66
Fractal 2
nd
-Order
Solution
Fractal
2
nd
-Order
Solution
(Kohlrausch
Function)
10
2
10
3
10
4
10
5
10
6
10
7
1
10
100
 = 0.66
Fractal
1
st
-Order
Solution
Fractal
2
nd
-Order
Solution
InducedLoss(dB/km)
Dose (rad)
Idealized Fractal Kinetics of Radiation-Induced Defect
Formation and Decay in Amorphous Insulators
During Irradiation After Cessation of Radiation
1st

25. 10
1
10
2
10
3
10
4
10
5
10
6
Time (s)
 = 0.66
Fractal 2
nd
-Order
Solution
Fractal
2
nd
-Order
Solution
(Kohlrausch
Function)
10
2
10
3
10
4
10
5
10
6
10
7
1
10
100
 = 0.66
Fractal
1
st
-Order
Solution
Fractal
2
nd
-Order
Solution
InducedLoss(dB/km)
Dose (rad)
During Irradiation After Cessation of Radiation
1st
Slope 
Slope -
Idealized Fractal Kinetics of Radiation-Induced Defect
Formation and Decay in Amorphous Insulators

26. 10
0
10
1
10
2
10
3
10
4
10
5
10
6
Factor of 4
No-Adjustable-Parameters
Prediction Based on
Fitted Growth Curve
Time (s)
10
1
10
2
10
3
10
4
10
5
10
6
10
7
1
10
Data
Fitted Decaying Part
Fitted Non-Decaying
Parts
InducedLoss(dB/km)
Dose (rad)
Fractal Kinetics of Radiation-Induced Defect
Formation and Decay in Amorphous Insulators: The Reality
C
B
B+C

27. 10
0
10
1
10
2
10
3
10
4
10
5
10
6
Factor of 4
No-Adjustable-Parameters
Prediction Based on
Fitted Growth Curve
Time (s)
10
1
10
2
10
3
10
4
10
5
10
6
10
7
1
10
Data
Fitted Decaying Part
Fitted Non-Decaying
Parts
InducedLoss(dB/km)
Dose (rad)
C
B
B+C
N.B. These data
prove the existence
of (non-decaying)
dose-rate independent
components.
Fractal Kinetics of Radiation-Induced Defect
Formation and Decay in Amorphous Insulators: The Reality

28. Fractal kinetics
of optical bands
in pure silica
glass…
0
5000
10000
15000
20000
25000
6,470 s
102 rad/s 15.3 rad/s
33
120
240
480
960 s 0
InducedAbsorption(dB/km)
400 500 600 700 800 900 1000 1100 1200 1300 1400 1500
0
500
1000
1500
2000
2500
Wavelength (nm)
N.B. These
bands appear
to arise from
self- trapped
holes.
Note absorption in all
three communications
windows.

29. Growth and Disappearance of “660- and 760-nm” Bands:
Optical Spectroscopy
D.L. Griscom, Appl. Phys. Lett. 71 (1997) 175
High-purity, low-OH,
low-Cl, pure-silica-core
fiber (KS-4V) under γ
irradiation for 240 s at
1.0 Gy/s
NBOHCs
760 nm
N.B. These results are
remarkably similar to
those for a low-OH, low-Cl
F-doped silica-core fiber
measured simultaneously.
660 nm
(Bands near 660, 760, and 900 nm are due to self-trapped holes.)

30. t-1
It appears that
the material is
“reconfigured”
by long-term,
low-dose-rate
irradiation in
such a way that
color centers
(STHs) are no
longer formed,
even when the
irradiation
continues
Loss at 760
nm during
γ irradiation
in the dark
at 1 Gy/s,
T=27 oC
Experimenter-Introduced
“Mid-Course” Transients
Growth and Disappearance of “660- and 760-nm” Bands:
Overview of Kinetics
D.L. Griscom, Appl. Phys. Lett. 71 (1997) 175
KS-4V, 760 nm

31. t-1
It appears that
the material is
“reconfigured”
by long-term,
low-dose-rate
irradiation in
such a way that
color centers
(STHs) are no
longer formed,
even when the
irradiation
continues – or
is repeated at a
later time.
Growth and Disappearance of “660- and 760-nm” Bands:
Overview of Kinetics
D.L. Griscom, Appl. Phys. Lett. 71 (1997) 175
Same Fiber Re-Irradiated
KS-4V, 760 nm

32. Growth and Disappearance of “660- and 760-nm” Bands:
Dose-Rate Dependence
D.L. Griscom, Phys. Rev. B64 (2001) 174201
100
1000
Stretched 2nd Order, =0.96
Stretched 2nd Order: =0.90
Kohlrausch: =0.95
Stretched 2nd Order: =0.53
Kohlrausch: =0.60
102 rad/s
15.3 rad/s
10
2
10
3
10
4
10
5
10
6
10
7
InducedLoss(dB/km)
Time (s)
…Dependent
Only on Time
(Not Dose Rate)
at Long Times!
Radiation
Bleaching
Large Initial
Dose-Rate
Dependence
Two Lengths of
Virgin Fiber,
Irradiated
Separately
KS-4V, 900 nm

33. Growth and Disappearance of “660- and 760-nm” Bands:
Optical Bleaching During Irradiation
D.L. Griscom, Phys. Rev. B64 (2001) 174201
100 1000
1000
10000
(a) Light On
F-Doped
KS-4V
InducedLoss(dB/km)
Time (s)
100 1000
 = 670 nm
(b) Light Off
535 rad/s
25 rad/s
Time (s)
 is independent of dose rate
in case of KS-4V core fiber.
 depends strongly on dose
rate but is independent of
the type of silica in the core.F-doped is slightly different.

34. Growth and Disappearance of “660- and 760-nm” Bands:
Isothermal Fading (Radiation Interupted), Regrowth
D.L. Griscom, Phys. Rev. B64 (2001) 174201
100 1000 10000
1000
10000
(a)
Stretched 2nd Order, =0.71
Kohlrausch, =0.52
InducedLoss(dB/km)
Time after Irradiation (s)
100 1000
(b)
F-Doped-Silica-Core Fiber,
Dose Rate = 102 rad/s
760 nm
Best Fits:
Stretched 2nd Order: =0.45
Kohlrausch: =0.53
660 nm
Best Fits:
Stretched 2nd Order: =0.60
Kohlrausch: =0.69
Irradiation Time (s)
Data Points for
t=0 were Used
in Fitting These
Data.
Fitted Values of
 Are Independent
of Wavelength.
Fitted Values of
 Are Strongly
Dependent on
Wavelength.
Fading Regrowth

35. Fractal-Kinetic Fitting Parameters (Both Orders)
Multi-Mode Low-OH, Low-Cl Pure-Silica-Core Fibers During  Irradiation
Data due to
Nagasawa et al.
(1984) pertain to
a silicone-clad
pure-silica core
fiber.
Gaussian
resolutions were
performed to
extract intensities
of the 660- and
760-nm bands
separately.
My data for F-
doped-silica-clad
pure-silica-core
fiber with an Al
jacket.
Measurements
were made at
fixed wavelengths
of 670 and 900
nm (no Gaussian
resolutions)
The same fiber
was subjected to
the 3 different
dose rates in
progression
beginning with
the lowest.
10 100 1000
1000
10000
Slope=1/2
Polymer-Clad
Silica-Core
Fiber KS-4V Silica-Core
Fiber, Aluminum
Jacketed
Slope=/2
Slope=
(c)
SaturationLoss(dB/km)
Dose Rate (rad/s)
10 100 1000
10
-4
10
-3
10
-2
Weighted Contributions
of Overlapping Bands
660-nm Band
Only
760-nm Band
Only
Slope=0.78(b)
RateCoefficient(1/s)
10 100 1000
0.5
0.6
0.7
0.8
0.9
1.0
=670 nm
Initial
Response
Recovery from
Optical Bleaching
Initial Response, =900 nm(a)
Exponent
•
•
•
Slope=0.78

k
Nsat

37. ÇA TERMINE MA DEUX-HEURS-LONG
PRESENTATION. EST-CE QUE IL Y A
DES QUESTIONS ?
C’EST EXPRÉS QUE VOTRE
PRESENTATION ÊTRE
INCOMPERHENSIBLE?
OU EST-CE QUE VOUS AVEZ
UN ESPÈS DE INCAPACITÉ «POWER
POINT» ?
EST-CE QUE IL Y A DES
QUESTIONS SUR LE
CONTENU ?
IL FUT DE
CONTENU ?