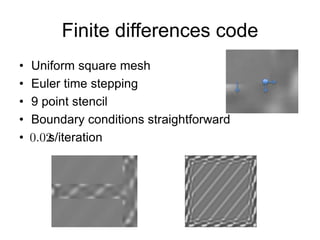
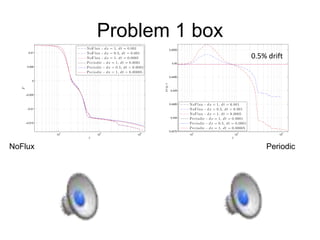
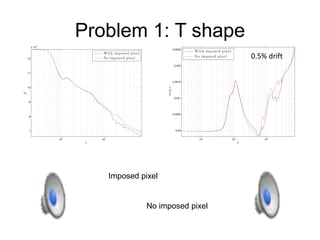
Gabriel Kocher, Matthew Seymour, and Nikolas Provatas from McGill University worked on spectral and finite difference methods for diffusion problems at a hackathon. Their spectral method using fast Fourier transforms parallelized easily but was unsuitable due to non-local operators causing crosstalk between boundaries. They then implemented a finite differences code on a uniform square mesh using Euler time stepping and a 9 point stencil, which had straightforward boundary conditions and a faster iteration time. They tested this method on diffusion problems in a box and T-shape domain with different boundary conditions and initial conditions, and compared concentration fields over time.

1. Hackathon results
Gabriel Kocher Matthew Seymour
Nikolas Provatas
McGill university

2. Spectral method - fail
• fft method parallelizes easily
• Naturally does periodic boundary conditions
• Attempt to shut off diffusion across boundaries
Non local operators still lead to crosstalk
Promote to

3. Finite differences code
• Uniform square mesh
• Euler time stepping
• 9 point stencil
• Boundary conditions straightforward
• s/iteration

4. Problem 1 box
NoFlux Periodic
0.5% drift

5. Problem 1: T shape
Imposed pixel
No imposed pixel
0.5% drift

6. Question 2 - Box
No flux
C field t=150
Periodic
C field t=150

7. Question 2
T boundary
C field t=150
Random init. cond.
C field t=150