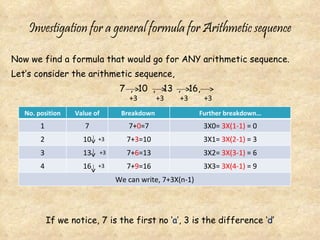
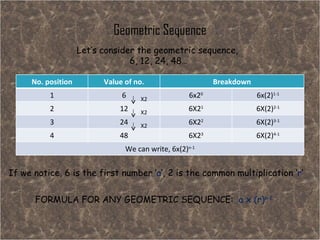
There are several common number patterns that follow specific rules. Square number sequences follow the rule of n^2, where the nth term is the square of n. Arithmetic sequences follow repetitive addition, where each term is created by adding a fixed number to the previous term. Geometric sequences follow repetitive multiplication, where each term is created by multiplying the previous term by a fixed number. The Fibonacci sequence is where each term is the sum of the two terms before it, starting with 1, 1. These patterns can be represented by general formulas to calculate any term in the sequence.

1. NUMBER PATTERN FORMULAS BY::NIKHIL

2. Pattern Patterns are about predicting what will come next. Patterns are seen everywhere from beautiful snowflakes to hexagonal honeycombs. In mathematics, a pattern is a sequence of numbers that follow a certain rule and procedure.

3. Types of number patterns Square number sequence Arithmetic sequence Geometric sequence Fibonacci sequence

4. Square Number Sequence An example square number sequence: 1, 4, 9, 16, 25, ? We notice that if we just square the number position, then we get the value: 1 2 ,2 2 , 3 2 , 4 2 , 5 2 , So the next number 6 2 =36. If we take ‘n’ as the number position, then the general formula to find any number’s position would be: n 2

5. Square Number Sequence Testing that the formula of the square number works: Given sequence: 100, 121, 144, ? Knowing that the 4 th number is the one we are going to find, Applying the formula, (n+9) 2 = (4+9) 2 =13 2 =169 Here, we added 9 to ‘n’ so that the number position would be correct.

6. A Closer look at Square number sequence… Let’s consider another set of square number. 400 , 441 , 484 , 529 …. It’s actually 20 2 , 21 2 , 22 2 , 23 2 …. Can be written as ( 1 +19) 2 , ( 2 +19) 2 , ( 3 +19) 2 , ( 4 +19) 2 .. We can replace the nos. in red with ‘n’, giving the formula: (n+19) 2 So the next (5 th ) number would be: (5+19) 2 = 576

7. Arithmetic Sequence Arithmetic sequence is a repetitive ADDITION of a fixed number to give the result. For example, 1 , 3 , 5 , 7 , … We know the next number ( 5 th number) would be 7+2 which is 9. But, what will be, say, the 10 th number? +2 +2 +2 +2 1st 2 nd 3 rd 4 th 5 th

8. Arithmetic Sequence: Exhibit 1 Let’s create a connection between the ‘Number position’ and the ‘Value of the number ’ If we replace the number position with ‘ n’ , we get a formula 2n-1 Using the formula, the value of the 10 th number is: 2X10-1 = 19 Checking, 1, 3, 5, 7, 9, 11, 13, 15, 17 , 19 X 2 -1 X 2 -1 X 2 -1 X 2 -1 Number position Value of the number 1 1 2 3 3 5 4 7

9. Arithmetic Sequence: Exhibit 2 Let’s look at another arithmetic sequence… 10, 15, 20, 25… If we replace the number position with ‘ n’ , we get a formula 5n+5 Using the formula, the value of the 10th number is: 5X10+5 = 55 Checking, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55 X 5 + 5 X 5 + 5 X 5 + 5 X 5 + 5 Number position Value of the number 1 10 2 15 3 20 4 25

10. Investigation for a general formula for Arithmetic sequence Now we find a formula that would go for ANY arithmetic sequence. Let’s consider the arithmetic sequence, 7 , 10 , 13 , 16, If we notice, 7 is the first no ‘ a ’, 3 is the difference ‘ d ’ FORMULA FOR ANY ARITHMETIC SEQUENCE: a + d(n-1) +3 +3 +3 +3 +3 +3 +3 No. position Value of no. Breakdown Further breakdown… 1 7 7+ 0 =7 3X0= 3X(1-1) = 0 2 10 7+ 3 =10 3X1= 3X(2-1) = 3 3 13 7+ 6 =13 3X2= 3X(3-1) = 6 4 16 7+ 9 =16 3X3= 3X(4-1) = 9 We can write, 7+3X(n-1)

11. Testing the formula From Exhibit 1: 1, 3, 5, 7,……… 19 Let’s use the formula and test if the 10th number in this arithmetic sequence is 19 a+d(n-1) = 1+2(10-1) =19 From Exhibit 2: 10, 15, 20, 25…… 55 Let’s use the formula and test if the 10th number in this arithmetic sequence is 55 a+d(n-1) = 10+5(10-1) =55

12. Geometric Sequence Geometric sequence is a repetitive MULTIPLICATION of a fixed number to give the result. For example, 5 , 10 , 20 , 40 , … We know the next number ( 5th number) would be 40x2 which is 80. But, what will be, say, the 10th number? 1st 2 nd 3 rd 4 th 5 th x2 x2 x2 x2

13. Geometric Sequence Let’s consider the geometric sequence, 6, 12, 24, 48… X2 X2 X2 If we notice, 6 is the first number ‘ a ’, 2 is the common multiplication ‘ r ’ FORMULA FOR ANY GEOMETRIC SEQUENCE: a x (r) n-1 No. position Value of no. Breakdown 1 6 6x2 0 6x(2) 1-1 2 12 6X2 1 6X(2) 2-1 3 24 6X2 2 6X(2) 3-1 4 48 6X2 3 6X(2) 4-1 We can write, 6x(2) n-1

14. Testing the formula Test 1: 4 , 12 , 36 , 108 , 324 Putting the formula and testing that the 5 th no. is 324, a x (r) n-1 = 4 X (3 )5-1 =324 x3 x3 x3 x3

15. Testing the formula Test 2: 2 , 10 , 50 , 250 , 1250 Putting the formula and testing that the 5th no. is 1250, a x (r) n-1 = 2 X (5) 5-1 =1250 x5 x5 x5 x5

16. Fibonacci Sequence ‘ Fibonacci’ was the nickname of an Italian mathematician Pisano Bogollo who lived between 1170 and 1250. He started the Fibonacci sequence for counting rabbit population. He was also given the credit of spreading in Europe the Hindu-Arabic number 1,2,3…, replacing the difficult-to-use Roman numbers such as I, II, III, IV.

17. Fibonacci Sequence The Fibonacci sequence is as follows.. 1, 1, 2, 3, 5, 8, 13, 21….. The next number is found by adding up the two numbers before it. For example: The 2 is found by adding the two numbers before it (1+1) Similarly, the 3 is just (1+2), And the 5 is just (2+3), and so on!

18. POP QUIZ

19. BIBLIOGRAPHY

20. Thank You