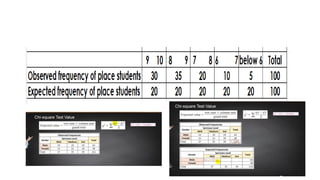
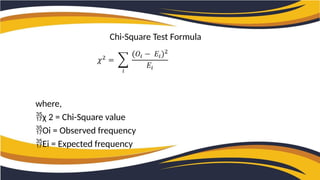
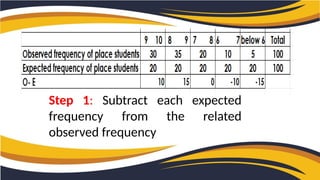
The document explains the chi-square test, a statistical method used to determine the association between two categorical variables. It covers three types: Pearson’s chi-square test, chi-square goodness of fit test, and chi-square test of independence, alongside the formula for calculating the chi-square value. A practical example illustrates how a researcher investigates the relationship between student placement rates and CGPA using the chi-square test.

1. chi- square
test

2. Objectives
•Understand what the chi-square test is and
how it works
•Learn about the different types of Chi-Square
tests
•Be able to calculate the chi-square value using
the chi-square formula

3. Statistical analysis is a key tool for making
sense of data and drawing meaningful
conclusions.

4. • is a statistical test used to determine if
there is a significant association between
two categorical variables.
• It is a non-parametric test, meaning it does not
make assumptions about the underlying
distribution of the data.
CHI- SQUARE TEST

5. There are three main types of chi-square tests commonly used in statistics:
1.Pearson’s Chi-Square Test: This test is used to determine if there is a
significant association between two categorical variables in a single
population. It compares the observed frequencies in a contingency table with
the expected frequencies assuming independence between the variables.
2.Chi-Square Goodness of Fit Test: This test is used to assess whether observed
categorical data follows an expected distribution. It compares the observed
frequencies with the expected frequencies specified by a hypothesized
distribution.
3.Chi-Square Test of Independence: This test is used to examine if there is a
significant association between two categorical variables in a sample from a
population. It compares the observed frequencies in a contingency table with
the expected frequencies assuming independence between the variables.

6. Chi-Square Test Formula
where,
χ 2 = Chi-Square value
Oi = Observed frequency
Ei = Expected frequency

7. A research scholar is interested in the relationship between the
placement of students in the statistics department of a reputed
University and their C.G.P.A (their final assessment score).
He obtains the placement records of the past five years from the
placement cell database (at random). He records how many
students who got placed fell into each of the following C.G.P.A.
categories – 9-10, 8-9, 7-8, 6-7, and below 6.
HO: There is no relationship between the placement rate and the
C.G.P.A.
H1: There is a statistically significant relationship between the
placement rate and the C.G.P.A of students

9. Chi-Square Test Formula
where,
χ 2 = Chi-Square value
Oi = Observed frequency
Ei = Expected frequency

10. Step 1: Subtract each expected
frequency from the related
observed frequency

11. Step 2: Square each value
obtained in step 1.

12. Step 3: Divide all the values
obtained in step 2 by the
related expected frequencies.

13. Step 4: Add all the values
obtained in step 3 to get the
chi-square test statistic value

14. Step 5: Once we have calculated the chi-square
value, we will compare it with the critical chi-
square statistic value
df= N-1 = 4

16. Therefore, we can say that the observed
frequencies from the sample data are significantly
different from the expected frequencies. In other
words, C.G.P.A is related to the number of
placements that occur in the department of
statistics.