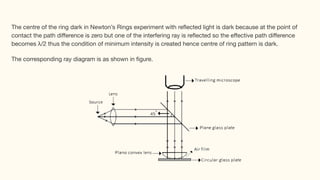
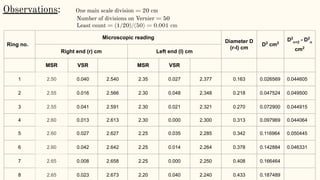
This document describes an experiment to observe and measure Newton's rings to determine the wavelength of sodium light. Key points: - Newton's rings are bright and dark interference rings formed between a plano-convex lens and glass plate due to varying film thickness. - The wavelength of light can be calculated using the diameter measurements of different rings and the lens's radius of curvature. - The experiment was performed and the wavelength of sodium light was calculated to be 5830.5 Angstroms with a 1.06% error from the standard value of 5893 Angstroms.

1. Newton’s Rings
By Divyansh
Dhanbir
Avneesh

2. Aim:
To set up and observe Newton’s
rings.
To determine the wavelength of
sodium light by Newton’s ring.

3. Apparatus
● Plano-convex lens of large
radius of curvature
● Optical arrangement for
Newton’s rings
● Plane glass plate
● Sodium lamp
● Travelling microscope

4. Formula used:
The wavelength λ of light is given by the formula:
λ = D²n+m
- D²n
4mR
Where, Dn+m
= diameter of (n+m)th ring
Dn
= diameter of nth ring
m = an integer number (of the rings)
R = radius of curvature of the curved face of the plano-convex lens.

5. Theory
The redistribution of energy by superposition of light waves is called as interference. The modification in
the distribution of intensity in the region of superposition is called as interference. Interference fringes are
alternately bright and dark patches of light obtained in the region of superposition. There is no loss of
energy in interference phenomenon, only redistribution of energy takes place. The energy absent at dark
places is actually present in bright regions. Alternate dark and bright rings formed due to presence of air
film when plano-convex lens is placed on glass plate are called Newton’s rings. When a plano-convex
surface is placed on a glass plate, an air film of gradually increasing thickness is formed. The thickness of
the air film is symmetrical and increases outwards from the point of contact. When monochromatic light is
allowed to fall normally on this air film and viewed in reflected light, alternate dark and bright rings are
observed. The rings are formed as a result of interference between light waves reflected from the upper
and lower surfaces of the air film developed between the convex surface of plano convex lens and plane
glass plate. This is so because the air film formed is wedge shaped and loci of points of equal thickness of
air film are circles concentric with point of contact. If 't' is the thickness of the air film at a point on the film,
the refracted wavelet from the lens has to travel a distance 't' into the film, and after reflection from the top
surface of the glass plate, it has to travel the same distance back to reach the point again. Thus, it travels a
total path '2t'. One of the two reflections takes place at the surface of the denser medium and hence it
introduces an additional phase change of π or an equivalent path difference λ/2 between two wavelets.

6. The centre of the ring dark in Newton’s Rings experiment with reflected light is dark because at the point of
contact the path difference is zero but one of the interfering ray is reflected so the effective path difference
becomes λ/2 thus the condition of minimum intensity is created hence centre of ring pattern is dark.
The corresponding ray diagram is as shown in figure.

7. Procedure
1. Click on the "light on" button.
2. Select the lens of desirable radius.
3. Adjust the microscope position to view the Newton rings.
4. Focus the microscope to view the rings clearly.
5. Fix the cross-wire on 20th
ring either from right or left of the centre dark ring and take the
readings .
6. Move the crosswire and take the reading of 18th
,16th
...........2nd
ring.
7. You have to take the reading of rings on either side of the centre dark ring.
8. Enter the readings in the tabular column.
9. Calculate the wavelength of the source by using the given formula.

8. Observations: One main scale division = 20 cm
Number of divisions on Vernier = 50
Least count = (1/20)/(50) = 0.001 cm
Ring no.
Microscopic reading
Diameter D
(r-l) cm
D2
cm2
D2
n+2
- D2
n
cm2
Right end (r) cm Left end (l) cm
MSR VSR MSR VSR
1 2.50 0.040 2.540 2.35 0.027 2.377 0.163 0.026569 0.044605
2 2.55 0.016 2.566 2.30 0.048 2.348 0.218 0.047524 0.049500
3 2.55 0.041 2.591 2.30 0.021 2.321 0.270 0.072900 0.044915
4 2.60 0.013 2.613 2.30 0.000 2.300 0.313 0.097969 0.044064
5 2.60 0.027 2.627 2.25 0.035 2.285 0.342 0.116964 0.050445
6 2.60 0.042 2.642 2.25 0.014 2.264 0.378 0.142884 0.046331
7 2.65 0.008 2.658 2.25 0.000 2.250 0.408 0.166464
8 2.65 0.023 2.673 2.20 0.040 2.240 0.433 0.187489

9. Calculations: Mean value of D2
n+2
- D2
n
= 0.046644 cm2
Wavelength of light λ = (D2
n+2
- D2
n
)/4mR
= (0.046644)/4(2)(100)
= 5830.5 Å
Result: Wavelength of light from the sodium light is found to be = 5830.5 Å
Standard mean wavelength = 5893 Å
Percentage error = (5830.5 - 5893) X 100
5893
= 1.06%

10. Sources of Error and Precautions:
i) Glass plates and lens should be cleaned thoroughly.
ii) The lens used should be of large radius of curvature.
iii) The source of light used should be an extended one.
iv) Before measuring the diameter of rings, the range of the microscope should be properly adjusted.
v) Crosswire should be focused on a bright ring tangentially.
vi) Radius of curvature should be measured accurately.

11. THANK YOU