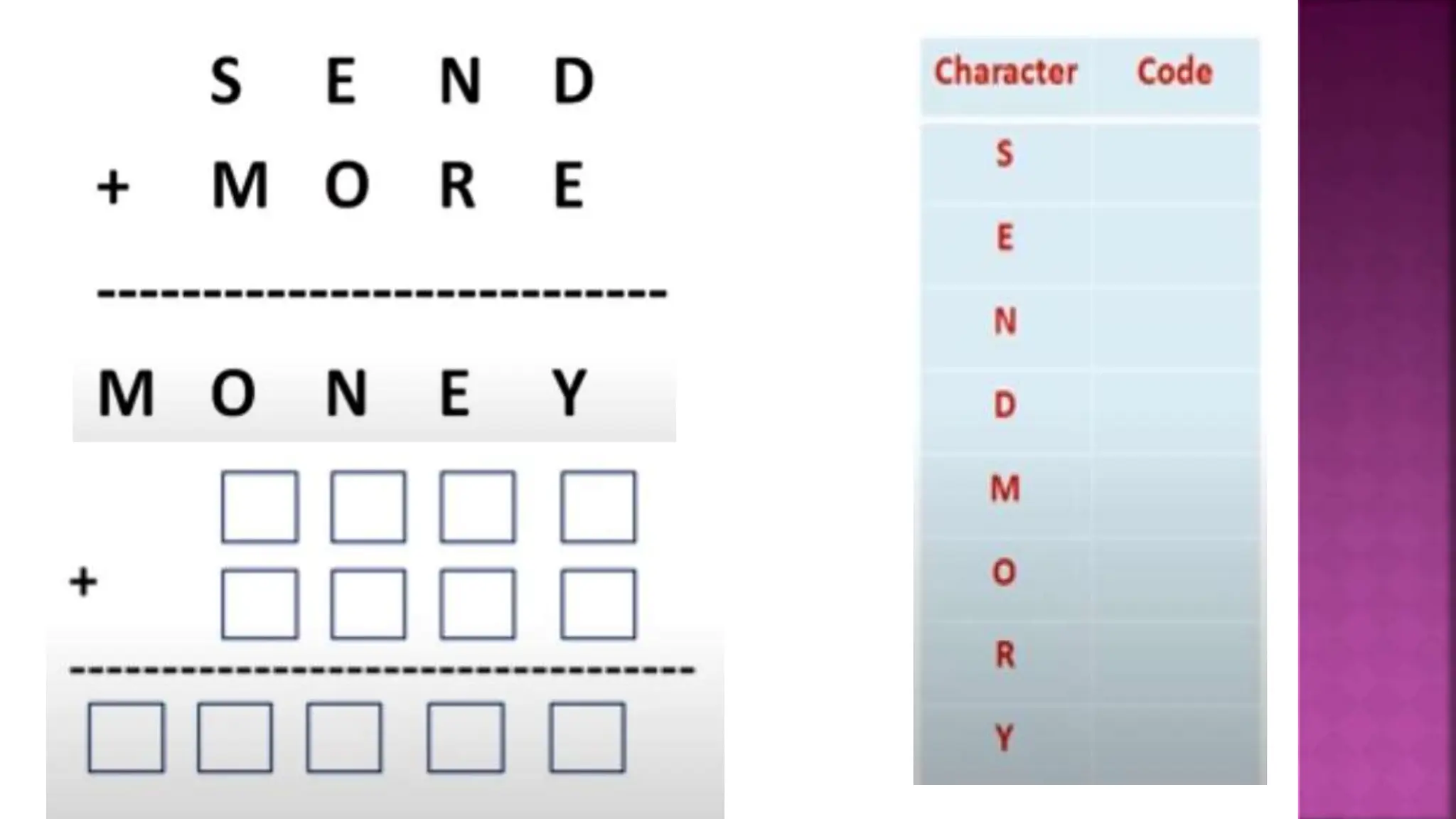
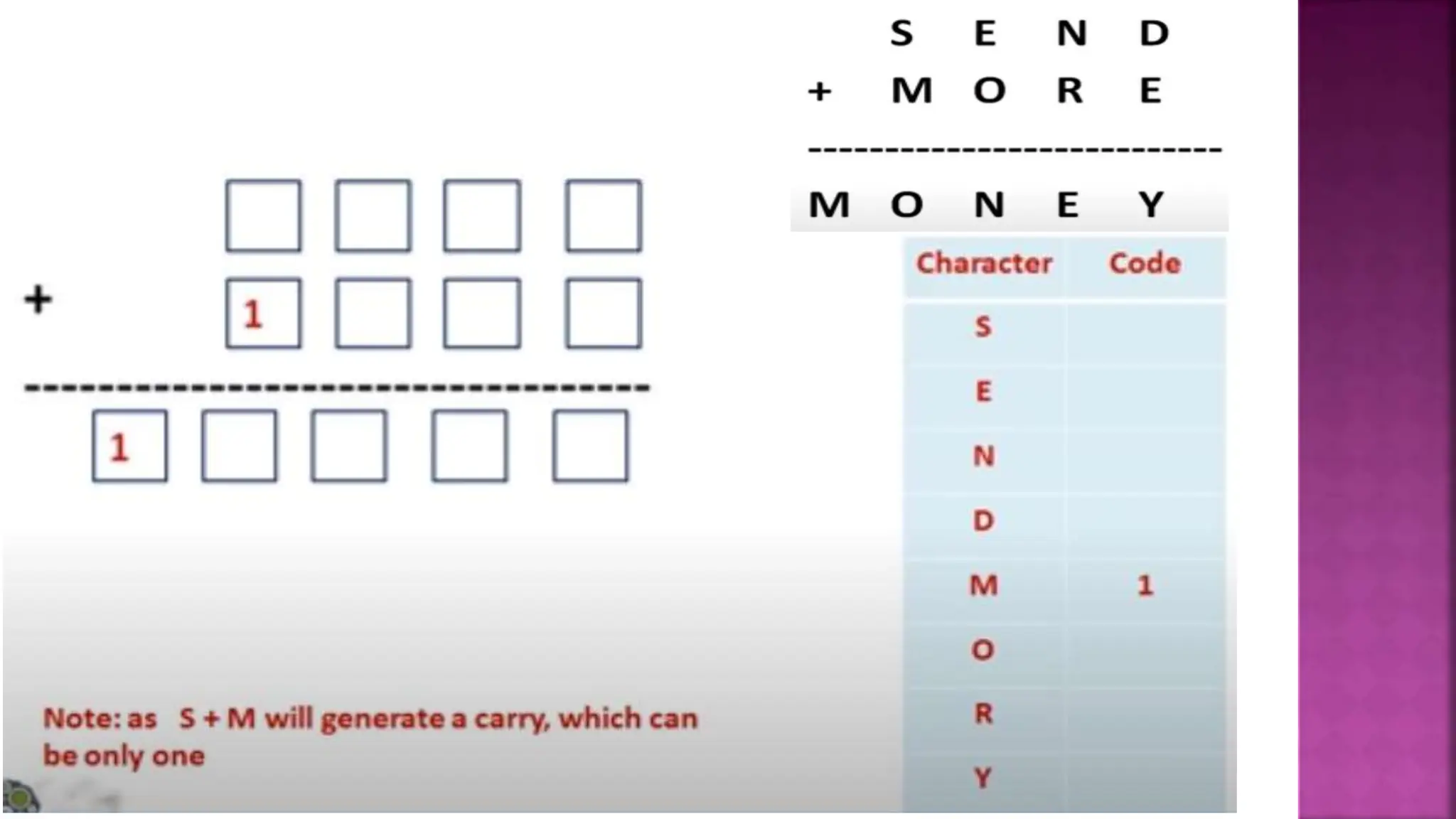
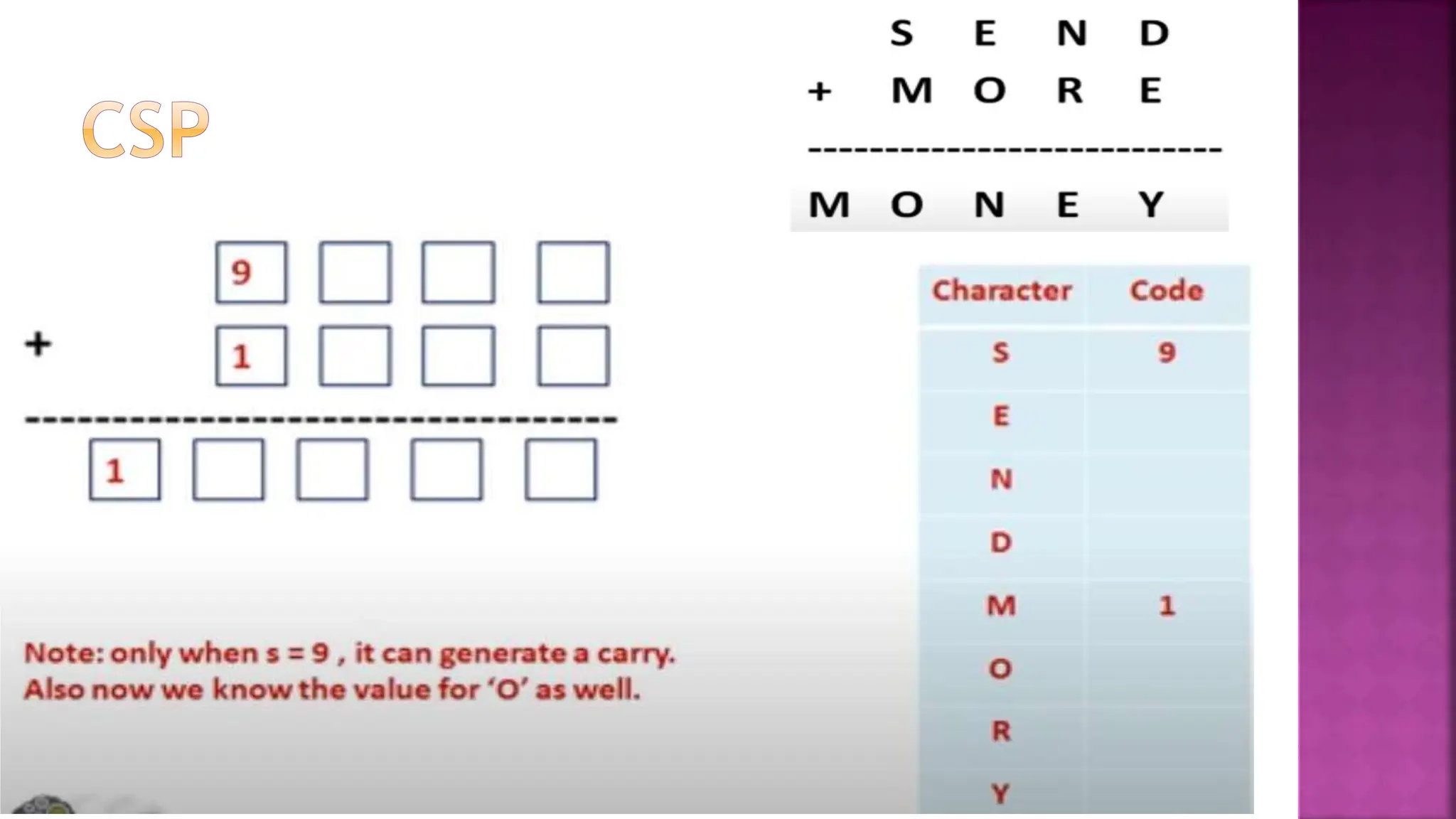
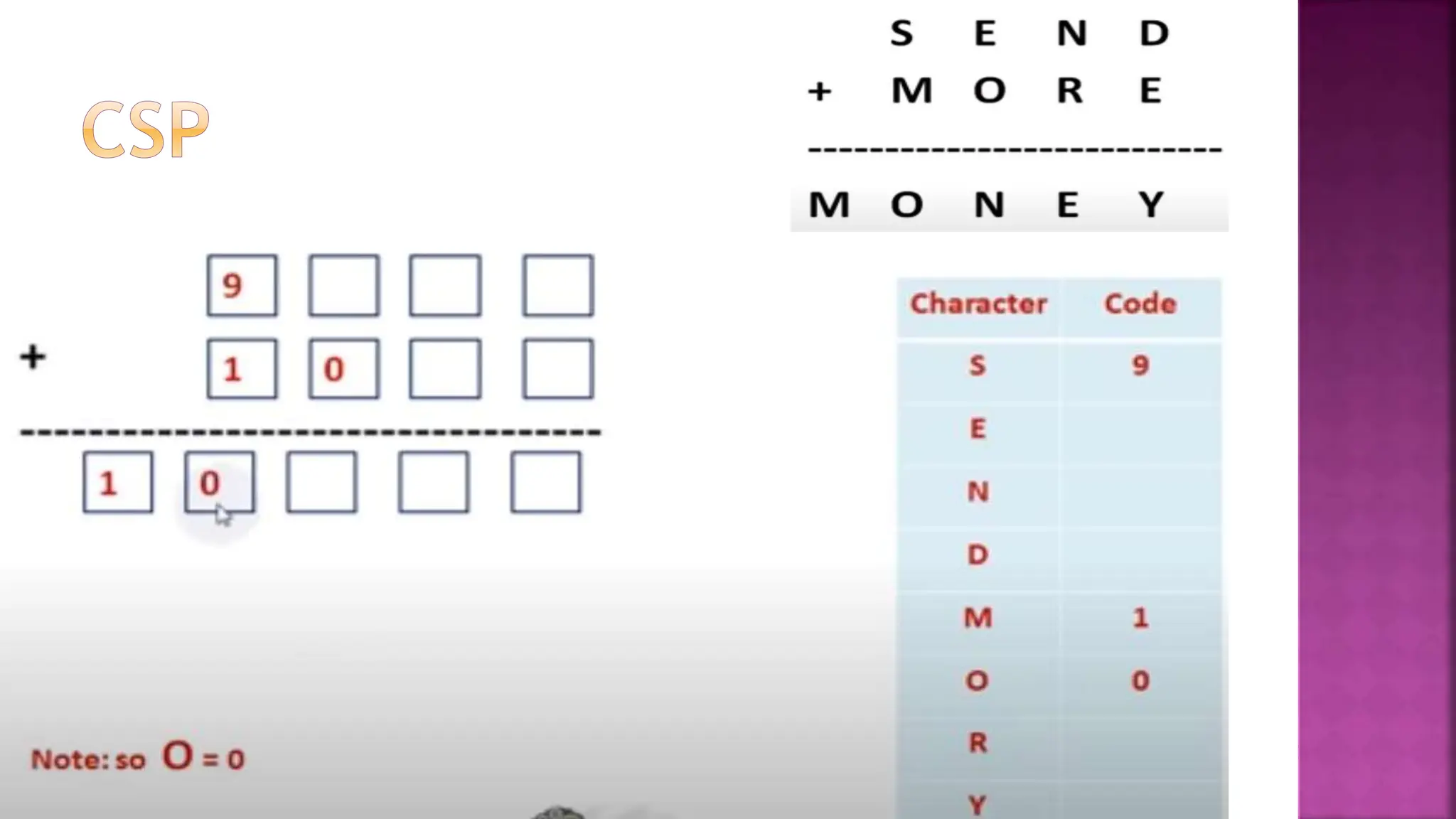
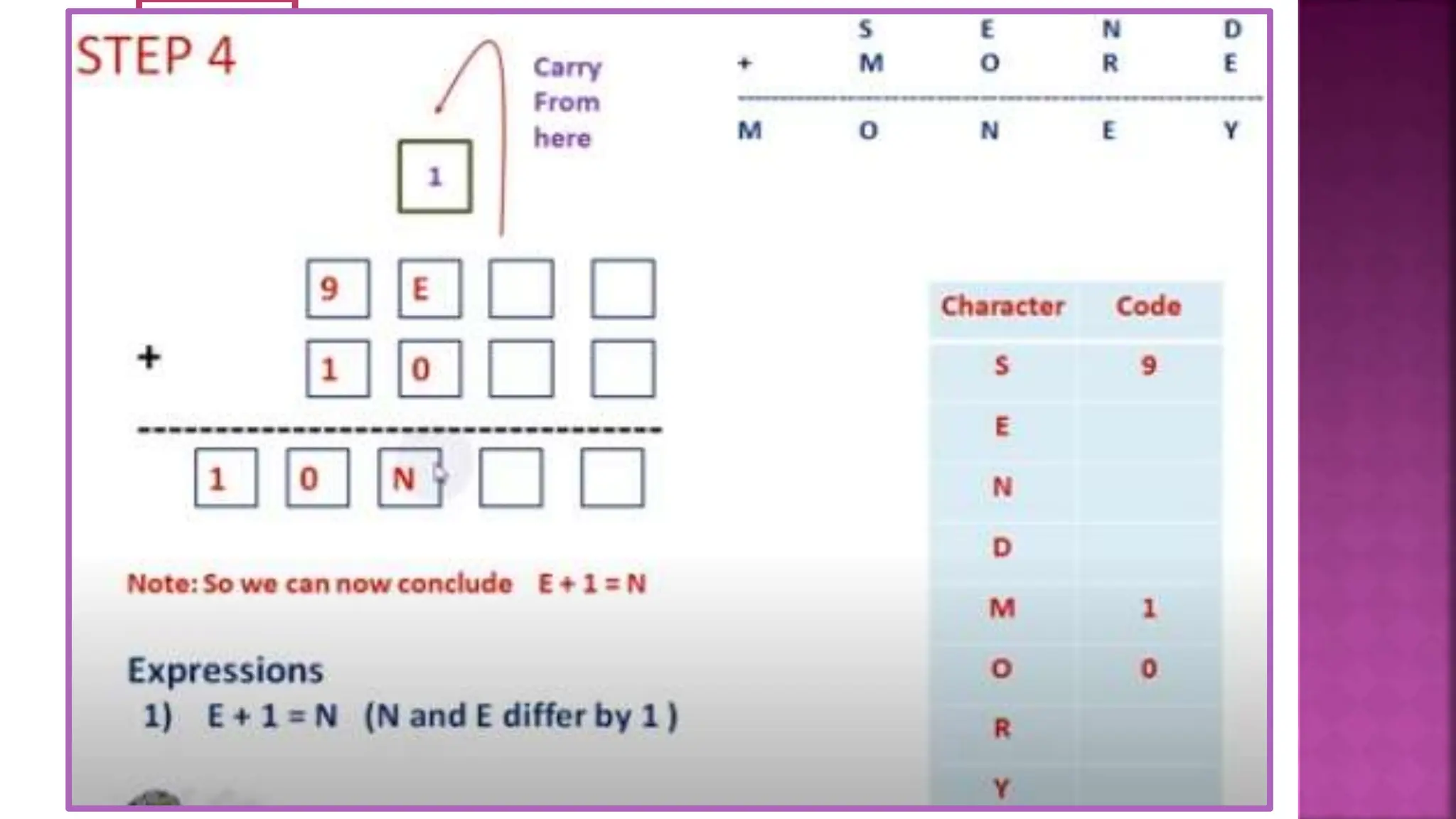
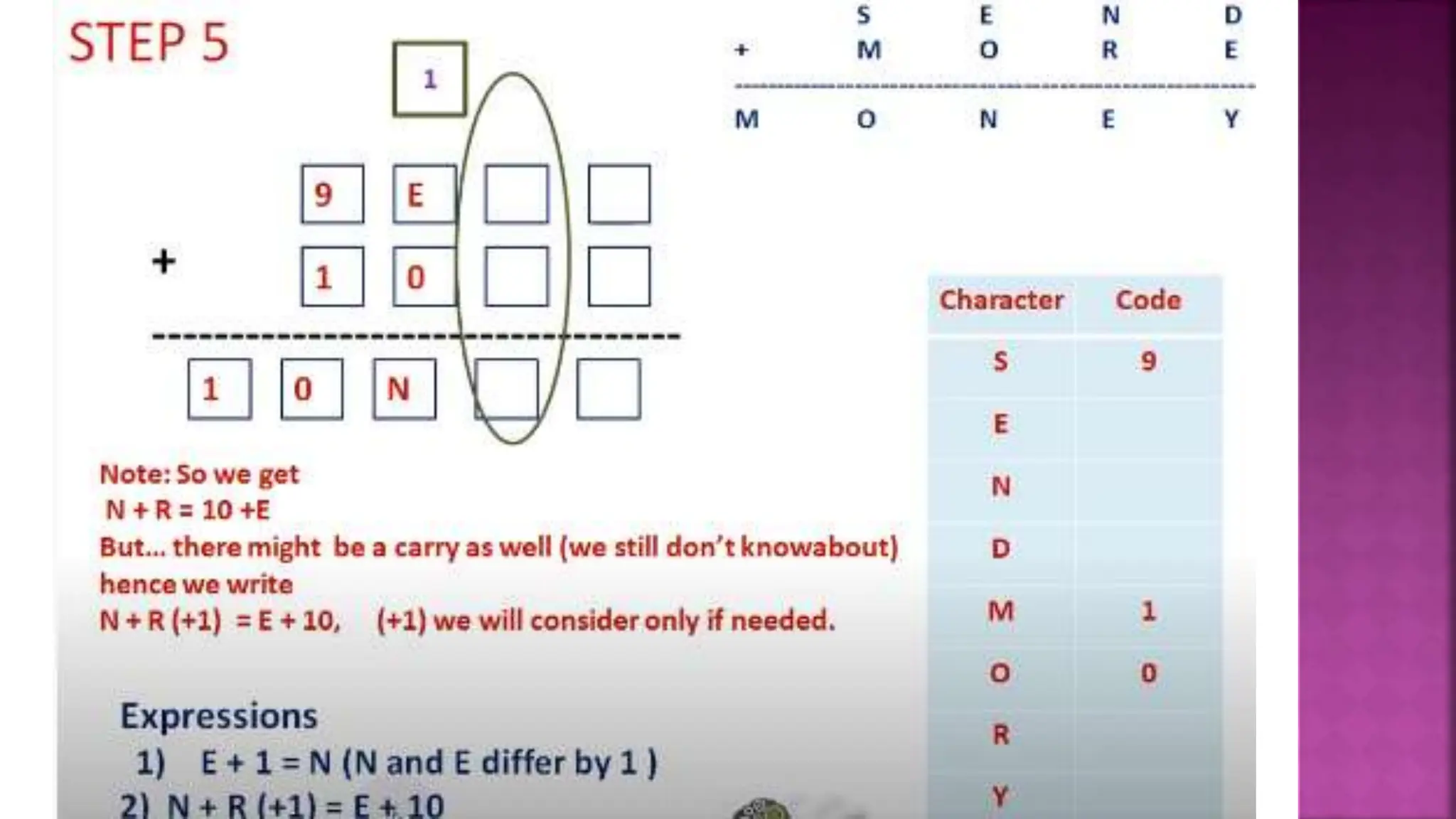
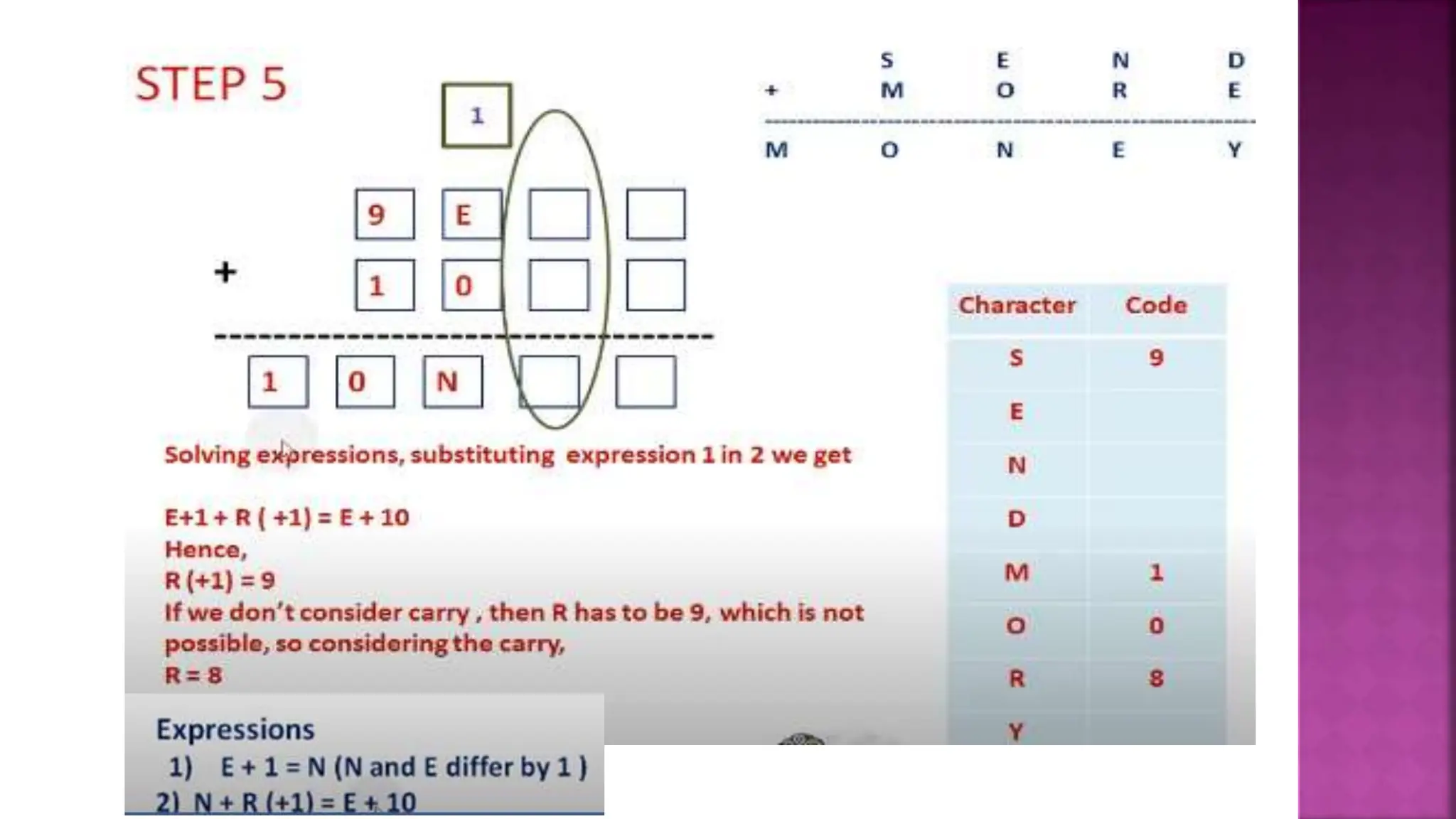
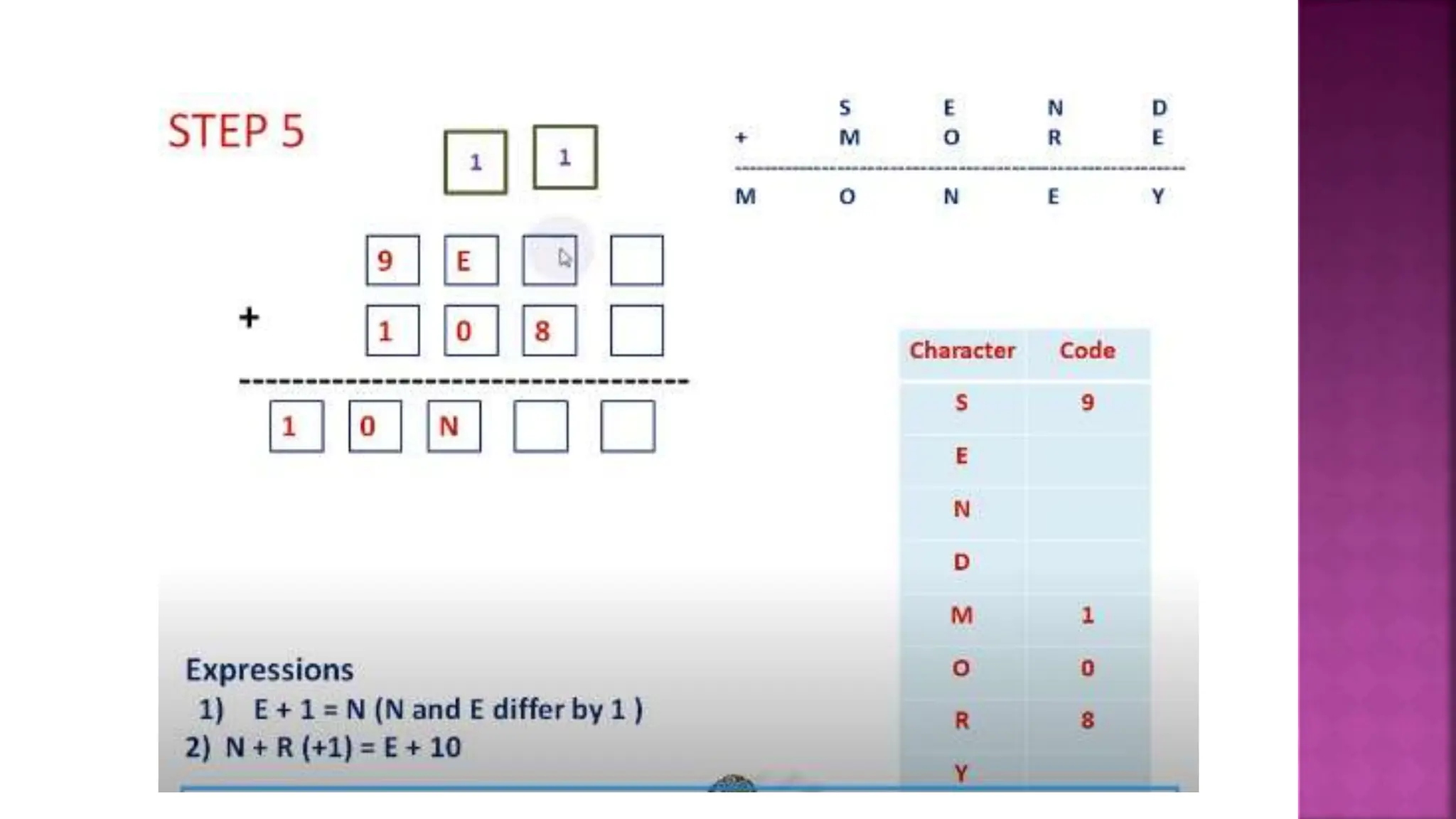
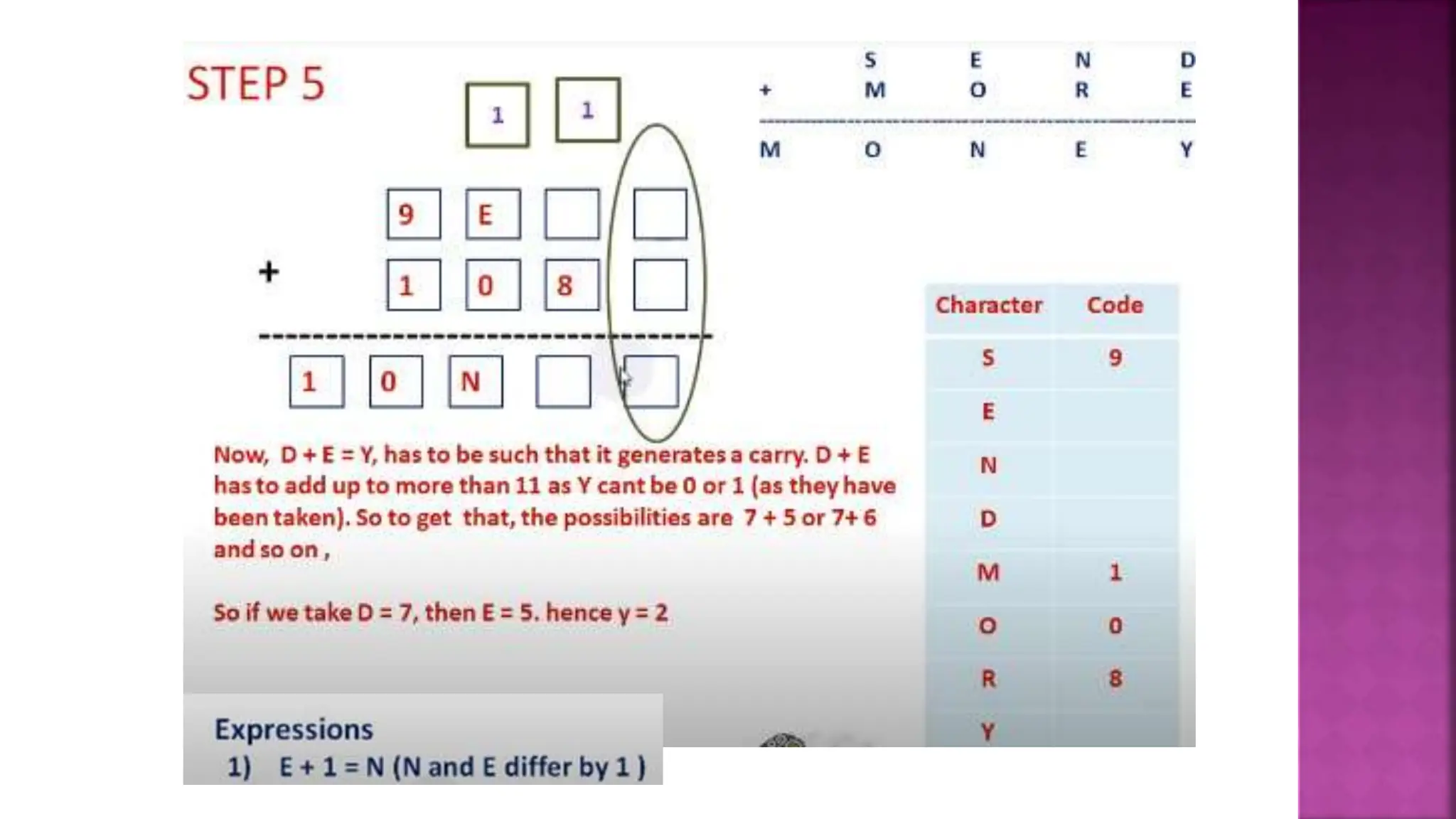
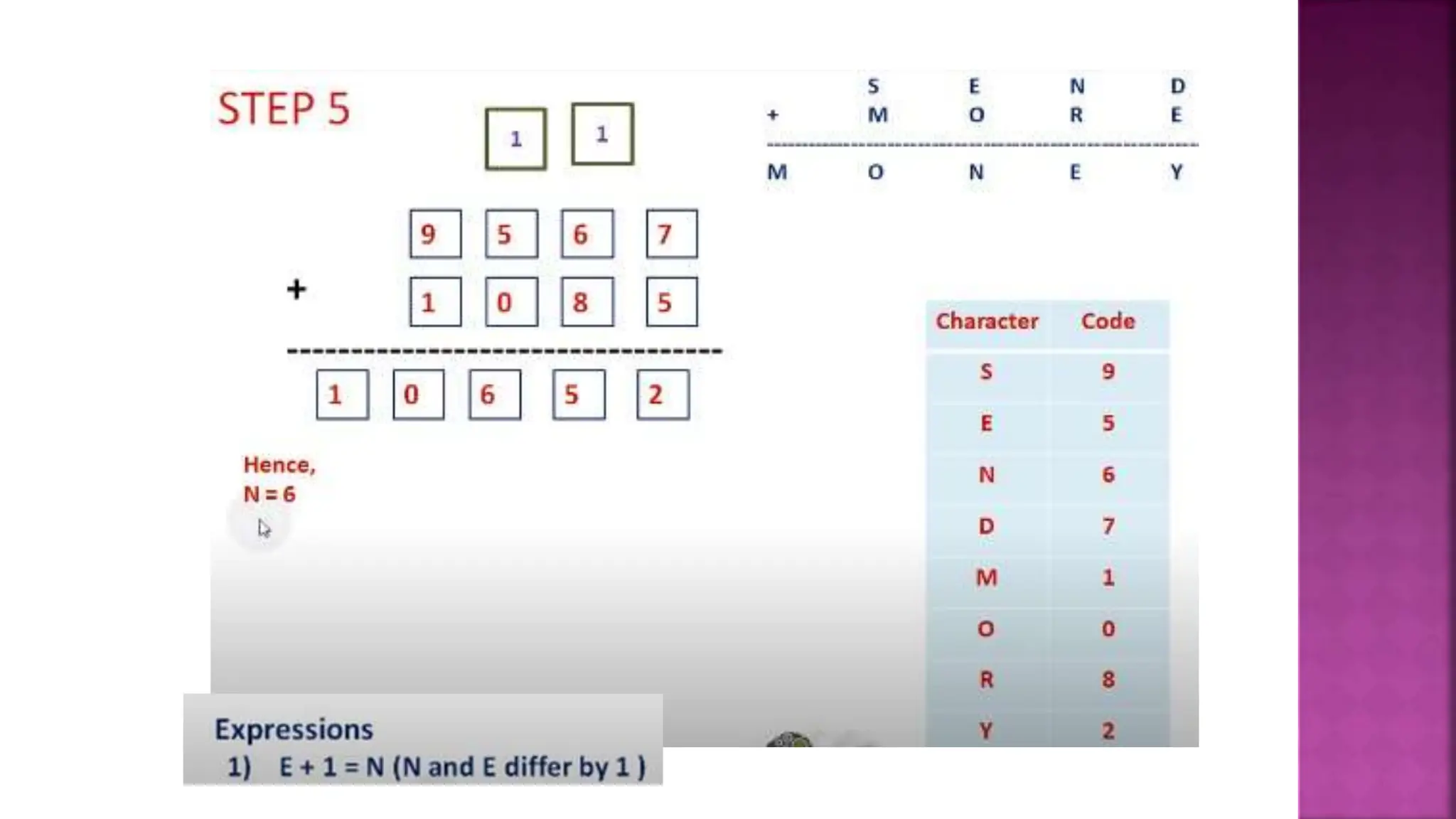
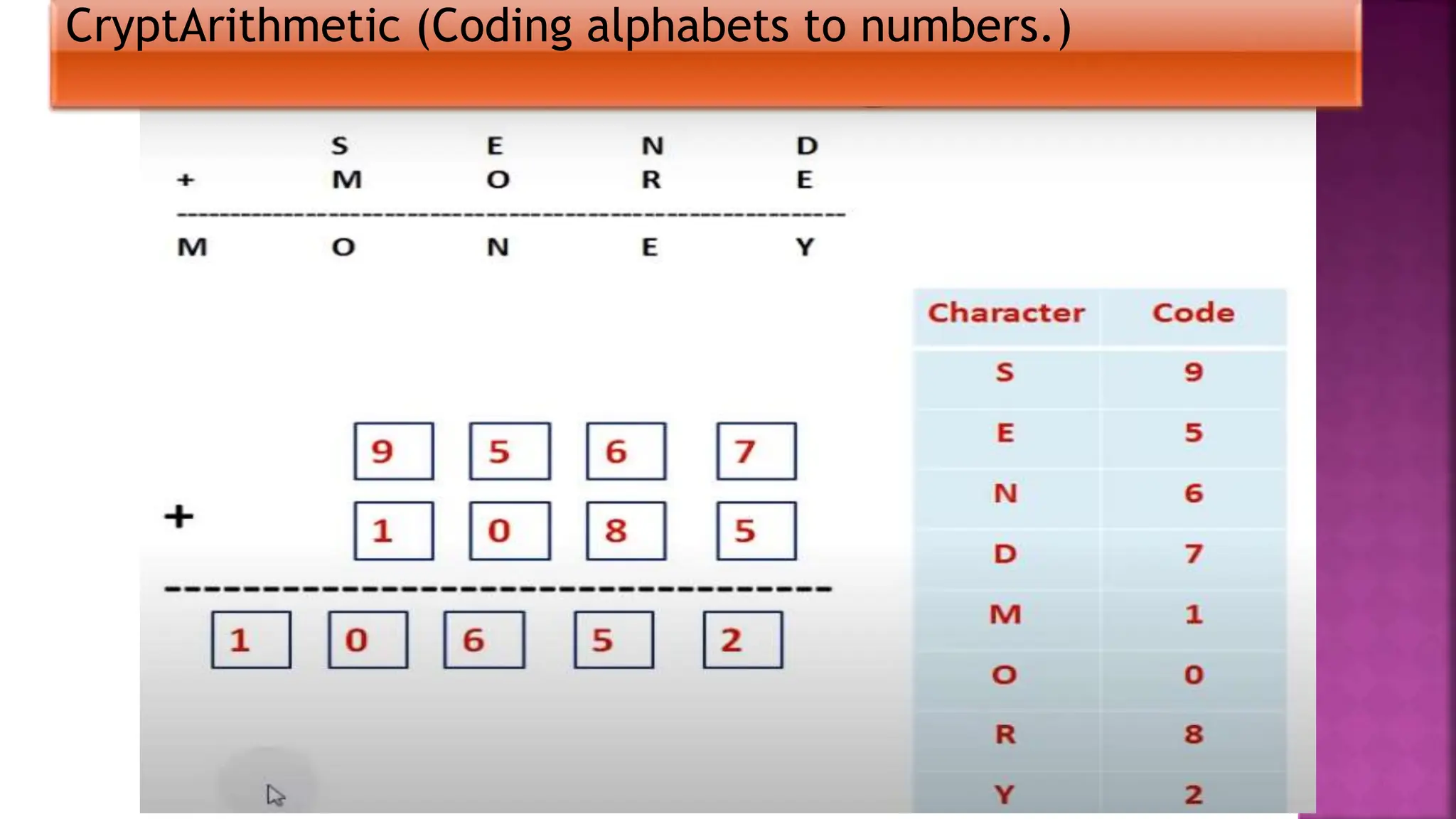
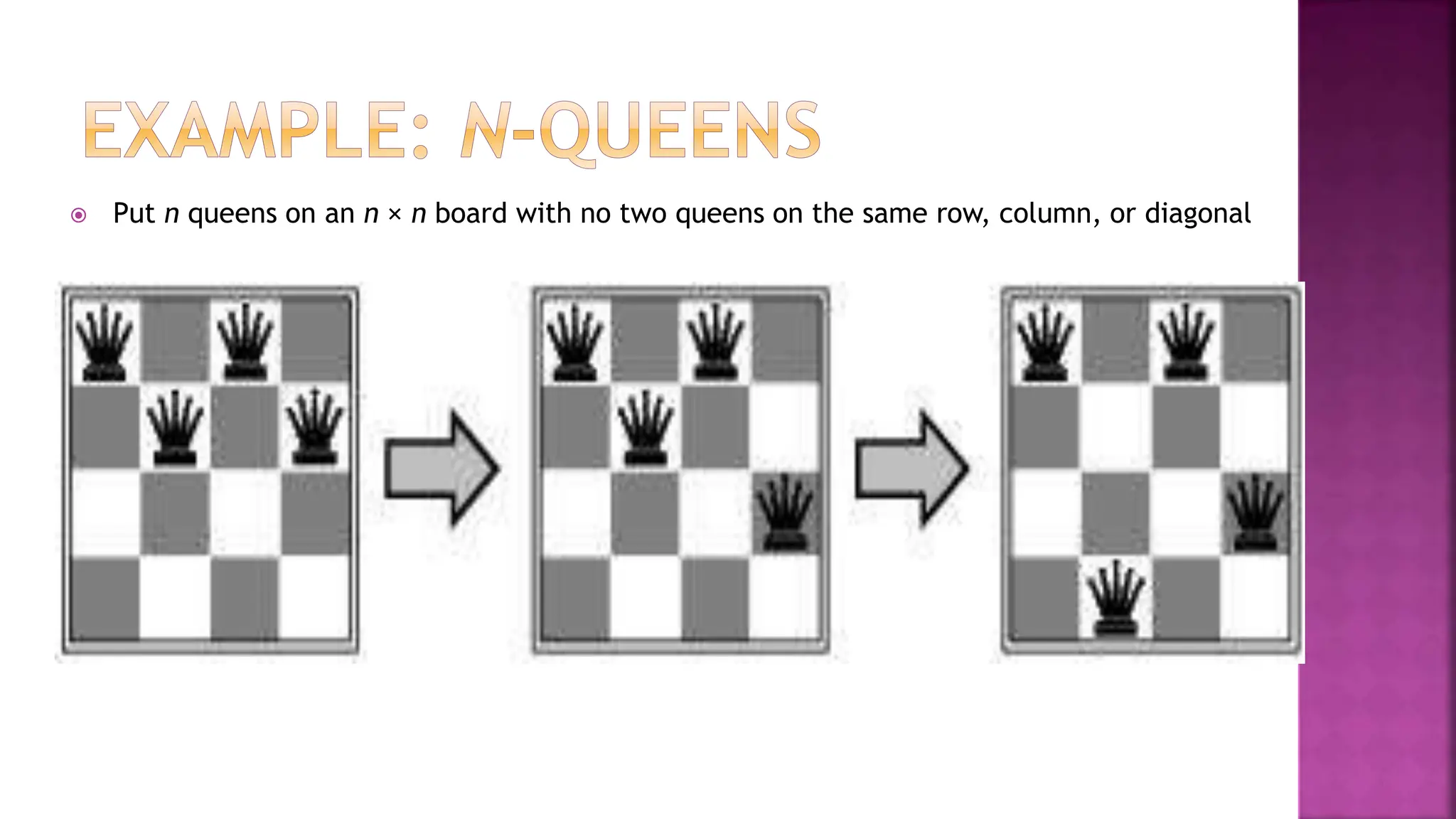
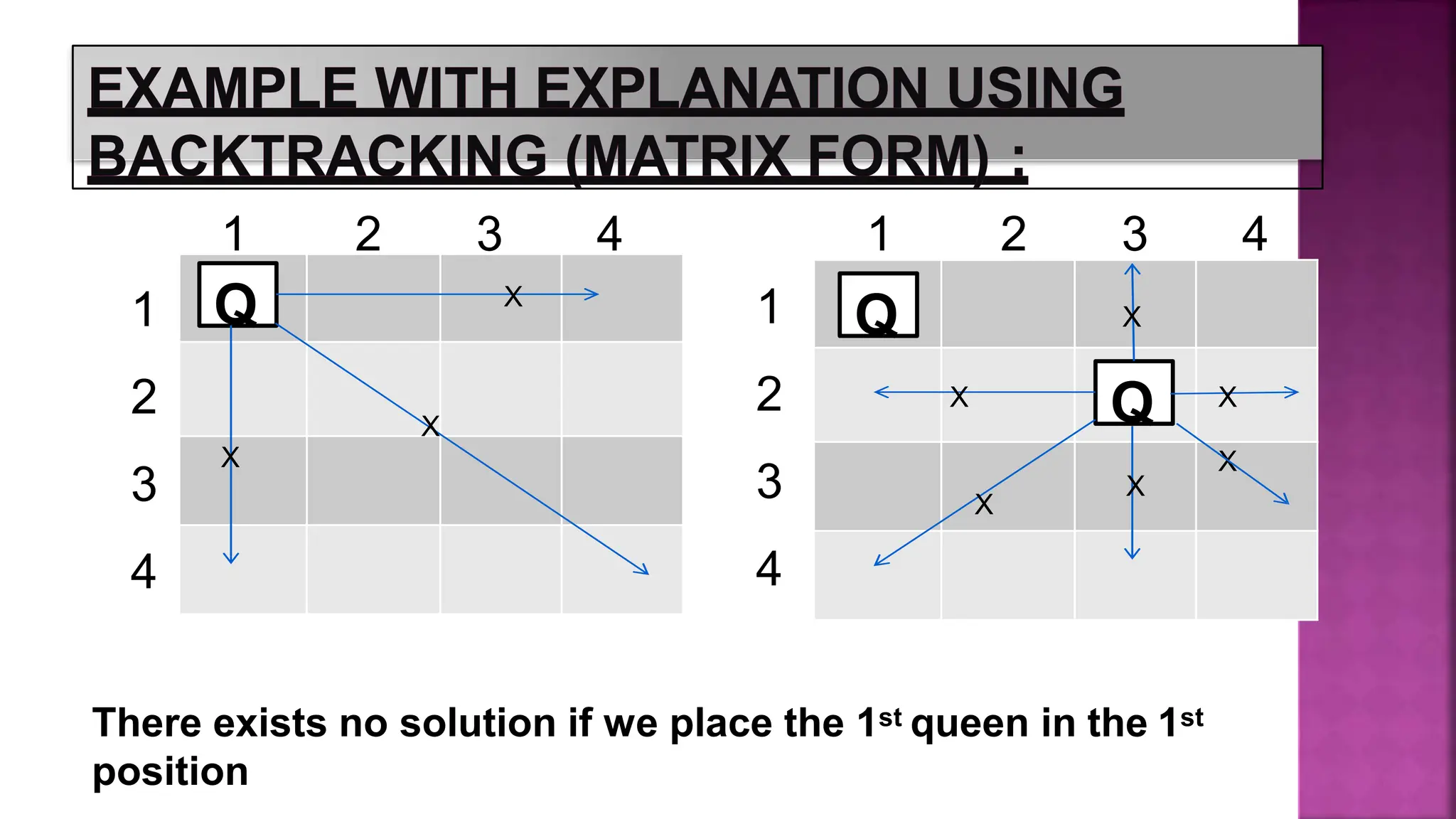
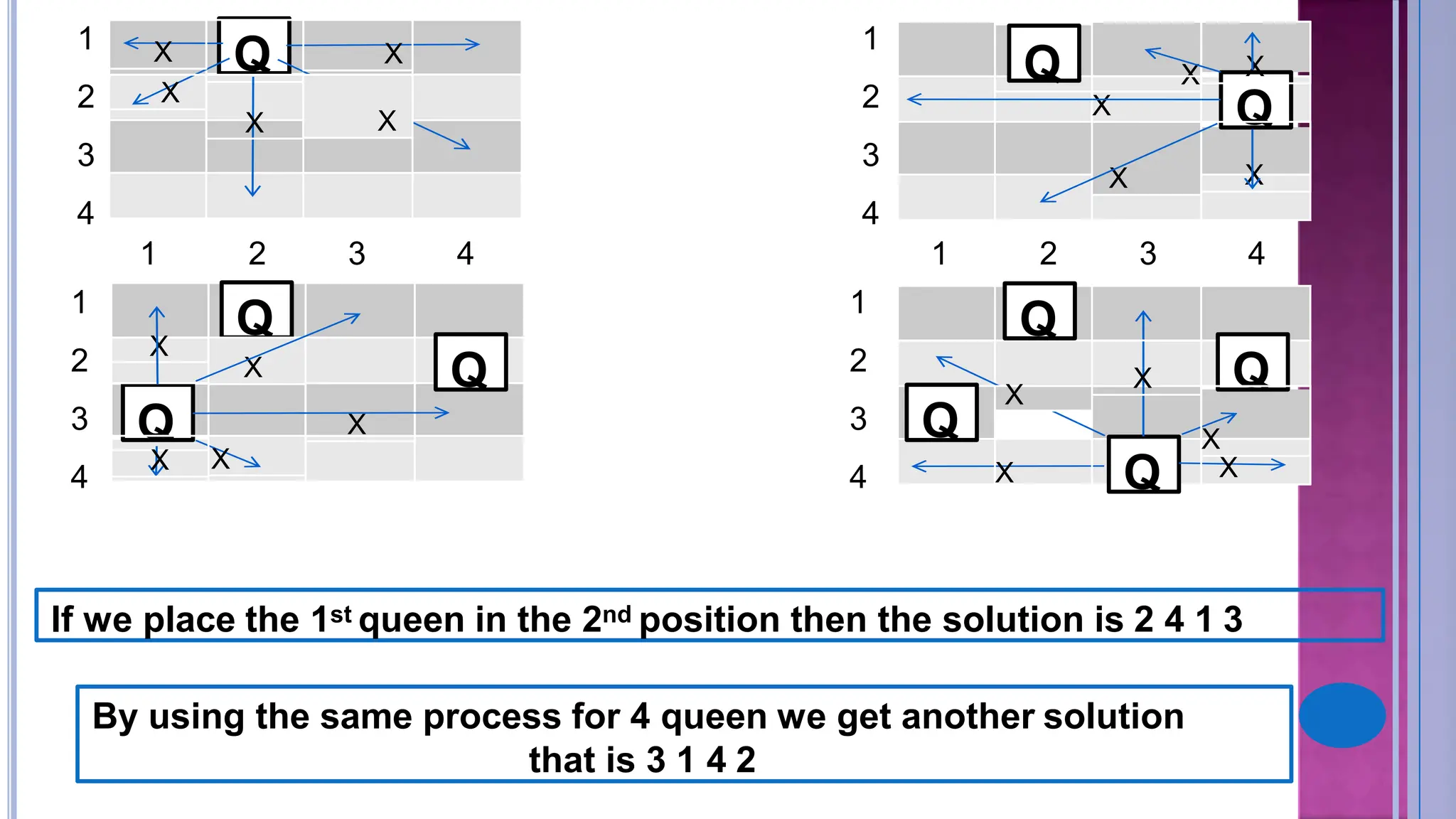
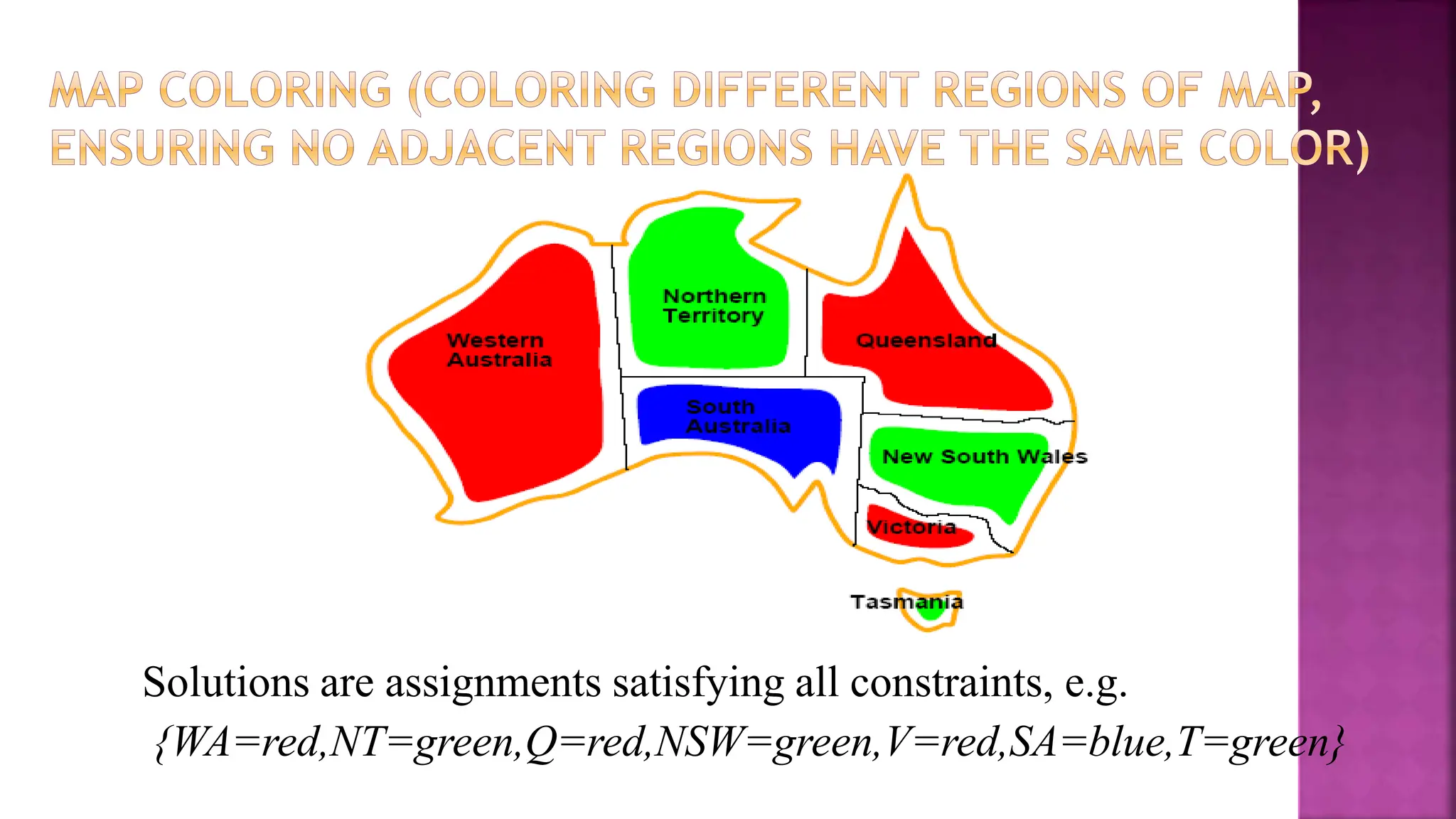
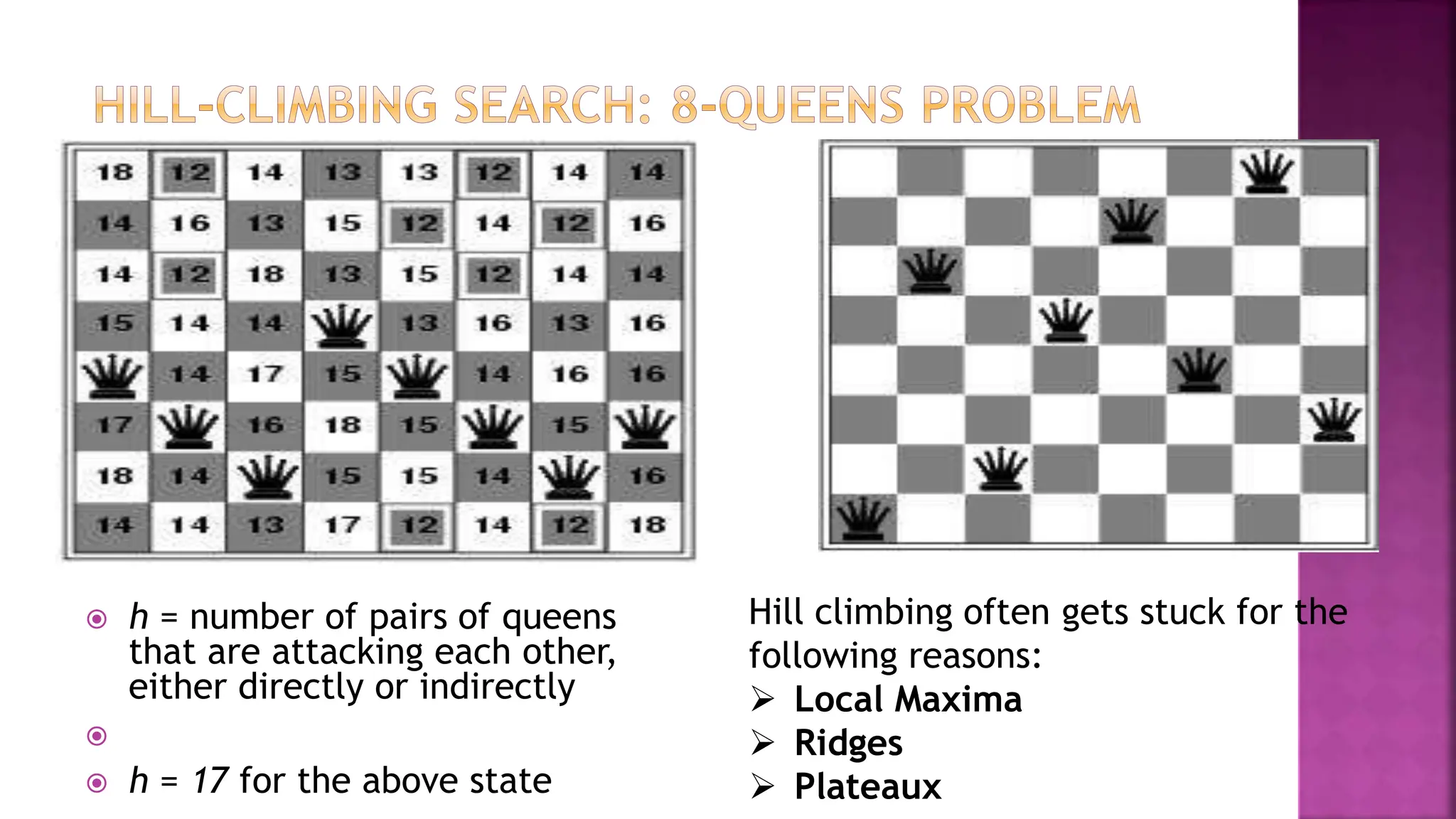
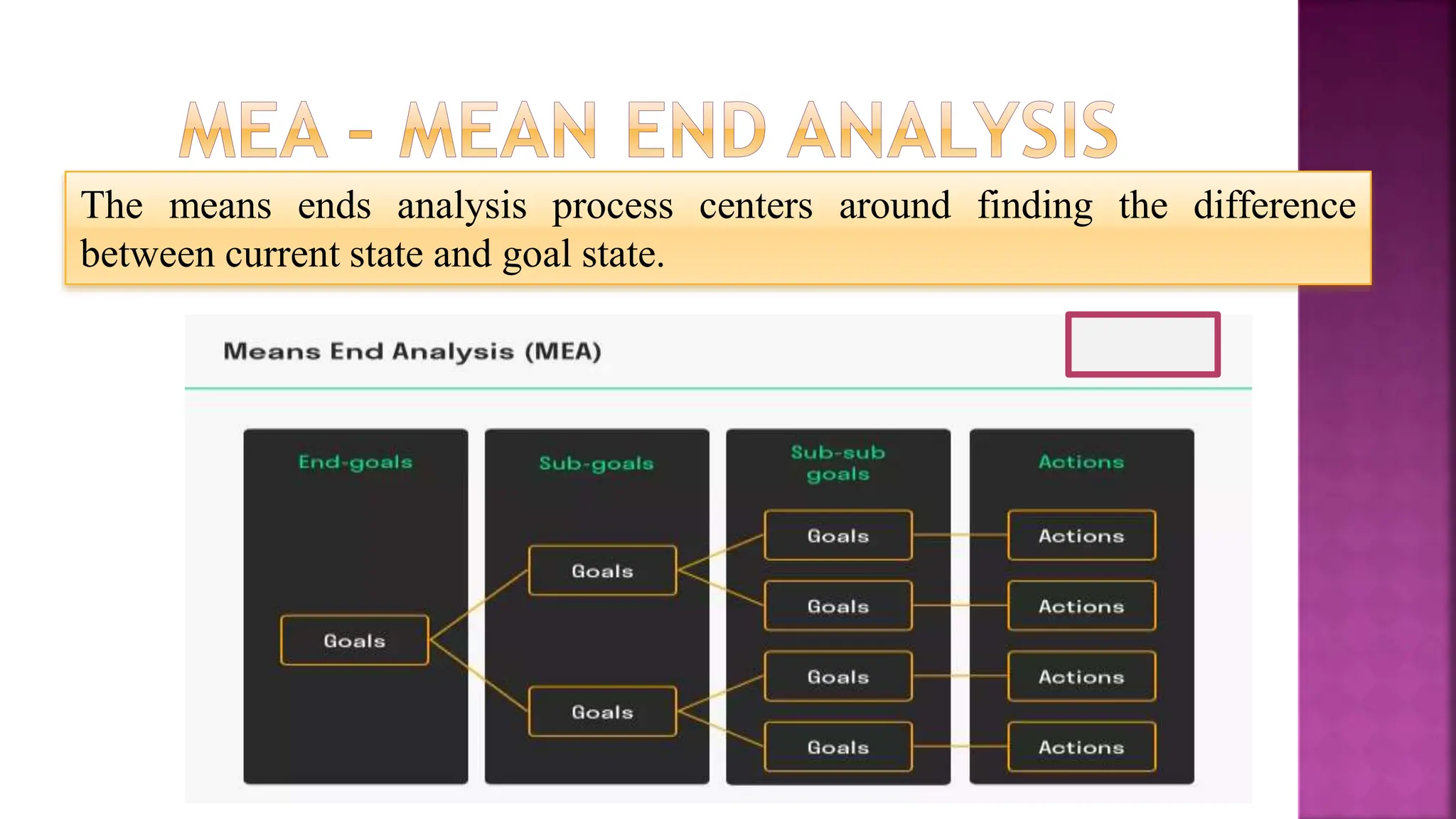
This document discusses constraint satisfaction problems and their solutions. It provides examples of constraint satisfaction problems like the n-queens problem, map coloring problem, cryptarithmetic puzzles, and Sudoku. It then explains the n-queens problem in more detail and provides an example of placing 4 queens on a 4x4 board with no attacks. Finally, it discusses solving constraint satisfaction problems using backtracking search and hill-climbing algorithms.

1. Presentation by
Dr. N. DANAPAQUIAME, Professor,
Mrs. C. KALPANA, Assistant Professor,
Mr. S. KUMARAKRISHNAN, Assistant Professor,
1
CONSTRAINT SATISFACTION PROBLEM

2.  A constraint satisfaction problem (CSP) is a problem that requires its solution
within some limitations or conditions also known as constraints. It consists of
the following:
 A finite set of variables which stores the solution (V = {V1, V2, V3,....., Vn})
 A set of discrete values known as domain from which the solution is picked
(D = {D1, D2, D3,.....,Dn})
 A finite set of constraints (C = {C1, C2, C3,......, Cn})
 In many optimization problems, the path to the goal is irrelevant; the goal
state itself is the solution
 State space = set of "complete" configurations
 Find configuration satisfying constraints, e.g., n-queens
 In such cases, we can use local search algorithms
 Keep a single "current" state, try to improve it

3.  CryptArithmetic (Coding alphabets to numbers.)
 n-Queen (In an n-queen problem, n queens should be placed in an
nXn matrix such that no queen shares the same row, column or
diagonal.)
 Map Coloring (coloring different regions of map, ensuring no
adjacent regions have the same color)
 Crossword (everyday puzzles appearing in newspapers)
 Sudoku (a number grid)
 Latin Square Problem

4.  Solve the following expression
CryptArithmetic (Coding alphabets to numbers.)

16. CryptArithmetic (Coding alphabets to numbers.)

17.  A=5
 D=2
 H=6
 M=3
 R=9
 T=4
 Y=0
 MATH = 3546, (+)
 MYTH = 3046,
 HARD = 6592

19.  Put n queens on an n × n board with no two queens on the same row, column, or diagonal

20. PROBLEM USING
BACKTRACKING

21. THE QUEEN OF A
CHESSBOARD

22. FRANZ NAUCK
The first solution for 8
queens were provided by
Franz Nauck in 1850. Nauck
also extended the puzzle to n-
queens problem (on an n by
n – a chessboard of arbitrary
size ).

23.  The N-Queens problem originates from a
question relating to Chess, The n-Queens
problem. Chess is played on an n × n grid, with
each piece taking up one cell. A queen is a piece
in chess that, in any given move, can move any
distance vertically, horizontally, or diagonally.
However, the queen cannot move more than one
direction per turn. It can only move one direction
per turn.

24. Q X
X
X Q
X
X
X
X
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4
X
X
There exists no solution if we place the 1st queen in the 1st
position
Q

25. 1 2 3 4
1
2
3
4
Q
1 2 3 4
1
2
3
4
1
2
3
4
1
2
3
4
If we place the 1st queen in the 2nd position then the solution is 2 4 1 3
By using the same process for 4 queen we get another solution
that is 3 1 4 2
Q
Q
Q
Q
Q
Q
Q
Q
Q
X X
X X
X
X
X
X
X
X
X
X
X
X
X X X
X
X
X

26. Variables: WA, NT, Q, NSW, V, SA, T
Domains: Di={red,green,blue}
Constraints:adjacent regions must have different colors.
E.g. WA  NT (if the language allows this)
E.g. (WA,NT)  {(red,green),(red,blue),(green,red),…}

27. Solutions are assignments satisfying all constraints, e.g.
{WA=red,NT=green,Q=red,NSW=green,V=red,SA=blue,T=green}

29.  "Like climbing Everest in thick fog with amnesia"
 The hill-climbing search algorithm is shown in the following function. It
is simply a loop that continually moves in the direction of increasing
value- that is, uphill. It terminates when it reaches a “peak” where no
neighbour has a higher value.
Problem: depending on initial state, can get stuck in local

30.  h = number of pairs of queens
that are attacking each other,
either directly or indirectly

 h = 17 for the above state
Hill climbing often gets stuck for the
following reasons:
 Local Maxima
 Ridges
 Plateaux

31. • The search space is small, and
– There are no other available techniques, or
– It is not worth the effort to develop a more efficient
technique
• The search space is large, and
– There is no other available techniques, and
– There exist “good” heuristics

32. The means ends analysis process centers around finding the difference
between current state and goal state.

33. Means- ends analysis I useful for many human planning activities.
Consider the example of planning for an office worker. Suppose we have
a different table of three rules:
If in our current state we are hungry, and in our goal state we are not
hungry, then either the "visit hotel" or "visit Canteen” operator is
recommended.
If our current state we do not have money, and if in your goal state we
have money, then the "Visit our bank" operator or the "Visit secretary"
operator is recommended.
If our current state we do not know where something is , need in our goal
state we do know, then either the "visit office enquiry" , "visit secretary"
or "visit coworker " operator is recommended.