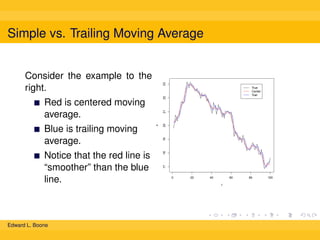
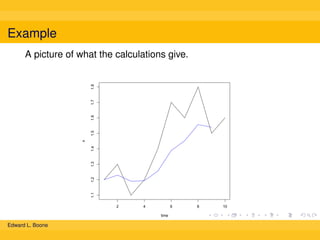
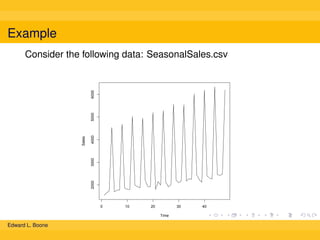
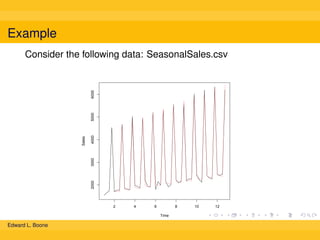
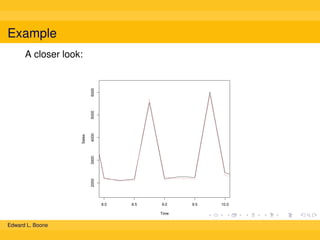
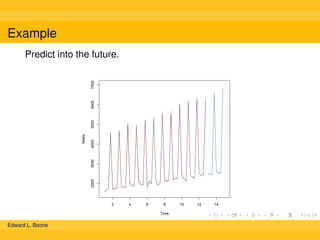
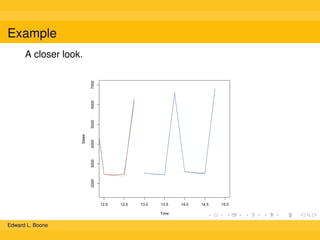
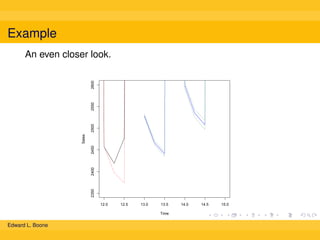
The document discusses different methods for calculating moving averages of time series data, including simple, trailing, and exponentially weighted moving averages. It also covers double and triple exponential smoothing techniques, which can model the level, trend, and seasonality components of time series. Triple exponential smoothing, also known as the Holt-Winters method, is demonstrated as an example using R code to analyze time series sales data and predict future values.

1. Moving Average Methods
Edward L. Boone
Department of Statistical Sciences and Operations Research
Virginia Commonwealth University
November 11, 2013
Edward L. Boone

2. Simple Moving Average
We are considering time series data xt where t = 1, 2, ..., T .
The order of the observations matter.
A simple moving average attempts to find a local mean.
This can be done simply by taking the average of the
points around the time of interest.
For example if we are interested in a window of width k we
simply take xt , xt−1 , xt+1 ,...,xt+k ,xt−k and compute their
average.
Edward L. Boone

3. Example
Consider the following example:
x1
1.2
x2
1.3
x3
1.1
x4
1.2
x5
1.4
x6
1.7
x7
1.6
x8
1.8
x9
1.5
x10
1.6
If we want the moving average at time t = 3 with window 2.
¯
x3,2 =
x1 + x2 + x3 + x4 + x5
1.2 + 1.3 + 1.1 + 1.2 + 1.4
=
= 1.24
5
5
If we want the moving average at time t = 7 with window 2.
¯
x7,2 =
x5 + x6 + x7 + x8 + x9
1.4 + 1.7 + 1.6 + 1.8 + 1.5
=
= 1.6
5
5
Notice that the “local” means are not similar.
Edward L. Boone

4. Trailing Moving Average
The problem with a standard moving average is that for the
mean at time t we need to know t + 1, t + 2,...,t + k , which is in
the future.
In many useful cases we don’t know the future.
We want to just use past values.
This leads to the idea of the trailing moving average.
Only take the average of xt−k , xt−k +1 ,...x1 , xt .
¯
xt,k =
Edward L. Boone
1
k
t
xt
i=t−k

5. Example
Again consider the following example.
x1
1.2
x2
1.3
x3
1.1
x4
1.2
x5
1.4
x6
1.7
x7
1.6
x8
1.8
x9
1.5
Trailing moving average with window k = 2
¯
x3,2 =
1.3 + 1.1 + 1.2
x2 + x3 + x4
=
= 1.2
3
3
.
.
.
x5 + x6 + x7
1.4 + 1.7 + 1.6
¯
=
=
= 1.56
3
3
¯
x4,2 =
¯
x7,2
Edward L. Boone
x1 + x2 + x3
1.2 + 1.3 + 1.1
=
= 1.2
3
3
x10
1.6

6. Simple vs. Trailing Moving Average
There are some issues that we will have to confront with all
time series methods.
How to handle the starting values?
Outliers?
Gaps?
Prediction?
Some of these are easier to deal with than others.
Edward L. Boone

7. Simple vs. Trailing Moving Average
23
Consider the example to the
right.
Edward L. Boone
22
x
20
19
18
17
Notice that the red line is
“smoother” than the blue
line.
21
Red is centered moving
average.
Blue is trailing moving
average.
True
Center
Trail
0
20
40
60
t
80
100

8. Issues with Moving Averages
Problems with simple moving average techniques.
In the previous methods, all observations in window get the
same weight.
We may wish to downweight observations as they get
farther in the past and always use all observations.
Gaps?
Prediction?
Some of these are easier to deal with than others.
Edward L. Boone

9. Exponentially Weighted Moving Average
A “simple” way to address the weighting problem is using a
weighted moving average.
There are several versions of these.
Each attempts to model the components of a time series
dataset.
If we just want to model the level then the Exponentially
Weighted Moving Average may be reasonable.
S1 = x1
St = αxt + (1 − α)St−1
These downweight the previous observations but still use
all observations.
Edward L. Boone

10. Example
Again consider the following example using α = 0.3.
x1
1.2
S1
S2
S3
S4
S5
S6
S7
S8
S9
S10
Edward L. Boone
=
=
=
=
=
=
=
=
=
=
x2
1.3
x3
1.1
x4
1.2
x1 = 1.2
αx2 + (1 − α)S1
αx3 + (1 − α)S2
αx4 + (1 − α)S3
αx5 + (1 − α)S4
αx6 + (1 − α)S5
αx7 + (1 − α)S6
αx8 + (1 − α)S7
αx9 + (1 − α)S8
??
x5
1.4
x6
1.7
x7
1.6
x8
1.8
x9
1.5
x10
1.6
= 0.3(1.3) + 0.7(1.2) = 1.23
= 0.3(1.1) + 0.7(1.23) = 1.191
= 0.3(1.2) + 0.7(1.191) = 1.1937
= 0.3(1.4) + 0.7(1.1937) = 1.2559
= 0.3(1.7) + 0.7(1.2559) = 1.3891
= 0.3(1.6) + 0.7(1.3891) = 1.4523
= 0.3(1.8) + 0.7(1.4523) = 1.5566
= 0.3(1.5) + 0.7(1.5566) = 1.5396

11. Example
1.1
1.2
1.3
1.4
x
1.5
1.6
1.7
1.8
A picture of what the calculations give.
2
4
6
time
Edward L. Boone
8
10

12. Exponentially Weighted Moving Average
What we have looked at so far is only concerned in estimating a
level (mean).
Only models the level.
We want to model the trend.
We want to model the Seasonality as well.
In order to do this we will need to build the model using
these basic components.
Edward L. Boone

13. Double Exponential Smoothing
Now we can add in a trend term bt .
Starting values:
S1 = x1
b1 = x2 − x1
Process smoothing:
St
bt
Edward L. Boone
= αxt + (1 − α)(St−1 + bt−1 )
= β(St − St−1 ) + (1 − β)bt−1

14. Example
Again consider the following example using α = 0.3 and
β = 0.2.
x1
1.2
x2
1.3
x3
1.1
x4
1.2
x5
1.4
x6
1.7
x7
1.6
x8
1.8
x9
1.5
S1 = x1 = 1.2
b1 = x2 − x1 = 1.3 − 1.2 = 0.1
S2 = αx2 + (1 − α)(S1 + b1 )
= 0.3(1.3) + 0.7(1.2 + 0.1) = 1.3
b2 = β(S1 − S2 ) + (1 − β)(b1 )
= 0.2(1.3 − 1.2) + 0.8(0.1) = 0.1
.
.
.
S10 = 1.7343
b10 = 0.0576
Edward L. Boone
x10
1.6

15. Example
Again consider the following example using α = 0.3 and
β = 0.2.
x1
1.2
x2
1.3
x3
1.1
x4
1.2
x5
1.4
x6
1.7
x7
1.6
x8
1.8
Predict x11 and x12 .
S10 = 1.7343
b10 = 0.0576
x11 = S10 + b10
= 1.7343 + 0.0567
= 1.7919
x12 = S10 + 2b10
= 1.7343 + 2(0.0567)
= 1.8496
Edward L. Boone
x9
1.5
x10
1.6

16. Triple Exponential Smoothing
To have a level, trend and season can get a bit complicated.
We need to know what period the seasonality manifests.
Quarterly data the seasonal “lag" L may be 4.
Monthly data the seasonal “lag" L may be 12.
Weekly data the seasonal “lag" L may be 52.
Daily data the seasonal “lag" L may be 365.
Think how complicated hourly data would be.
For simplicity we will consider Quarterly data with L = 4.
Edward L. Boone

17. Triple Exponential Smoothing
This is also known as the Holt-Winters method.
Process smoothing:
xt
+ (1 − α)(St−1 + bt−1 )
St = α
Ct−L
bt = β(St − St−1 ) + (1 − β)bt−1
xt
Ct = γ + (1 − γ)Ct−L
st
Starting values:
These are more difficult to get.
Some use the first few cycles and get means.
Some use regression to get S0 and b0 , then use those to
get the initial C’s.
We will let R do this for us so we don’t have to worry about
it.
Edward L. Boone

18. Example
4000
2000
3000
Sales
5000
6000
Consider the following data: SeasonalSales.csv
0
10
20
30
Time
Edward L. Boone
40

19. HoltWinters Function in R
Using the HoltWinters function in R we can estimate:
smoothing parameters
fitted values
the fitted values also contain the level, trend and seasonal
components
Edward L. Boone

20. Example
4000
2000
3000
Sales
5000
6000
Consider the following data: SeasonalSales.csv
2
4
6
8
Time
Edward L. Boone
10
12

21. Example
4000
2000
3000
Sales
5000
6000
A closer look:
8.0
8.5
9.0
Time
Edward L. Boone
9.5
10.0

22. Example
Sales
2000
3000
4000
5000
6000
7000
Predict into the future.
2
4
6
8
Time
Edward L. Boone
10
12
14

23. Example
Sales
2000
3000
4000
5000
6000
7000
A closer look.
12.0
12.5
13.0
13.5
Time
Edward L. Boone
14.0
14.5
15.0

24. Example
2350
2400
2450
Sales
2500
2550
2600
An even closer look.
12.0
12.5
13.0
13.5
Time
Edward L. Boone
14.0
14.5
15.0

25. Conclusion
Moving average and “smoothing" methods are ad hoc methods
for analyzing time series data.
MA methods require user input k .
Smoothing methods downweight past observations.
These methods can directly model the level, trend and
season components.
Since they are ad hoc they can produce odd results at
times.
While these methods are useful we need to be careful because
they have no clear theory to back them up.
Edward L. Boone