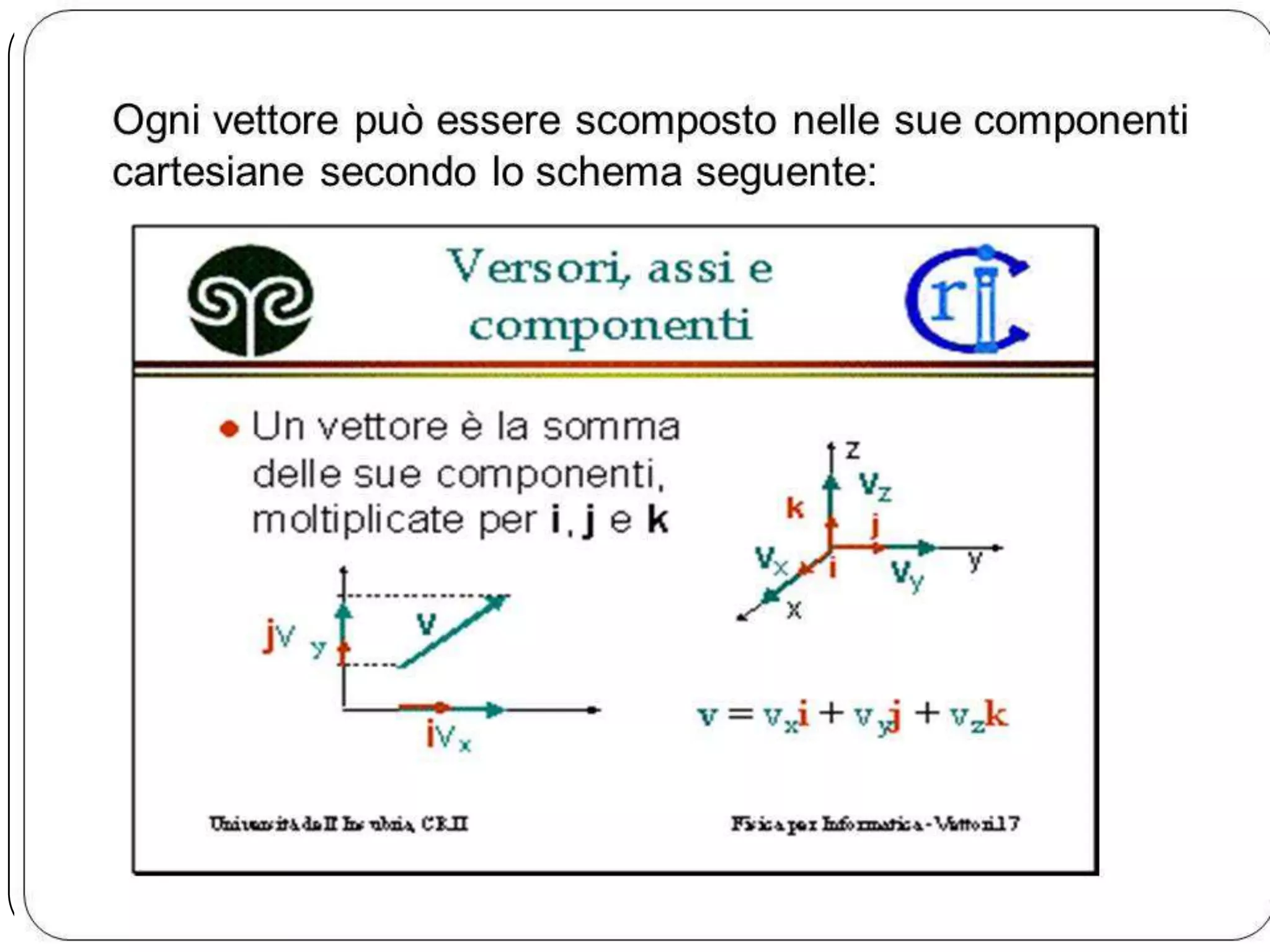
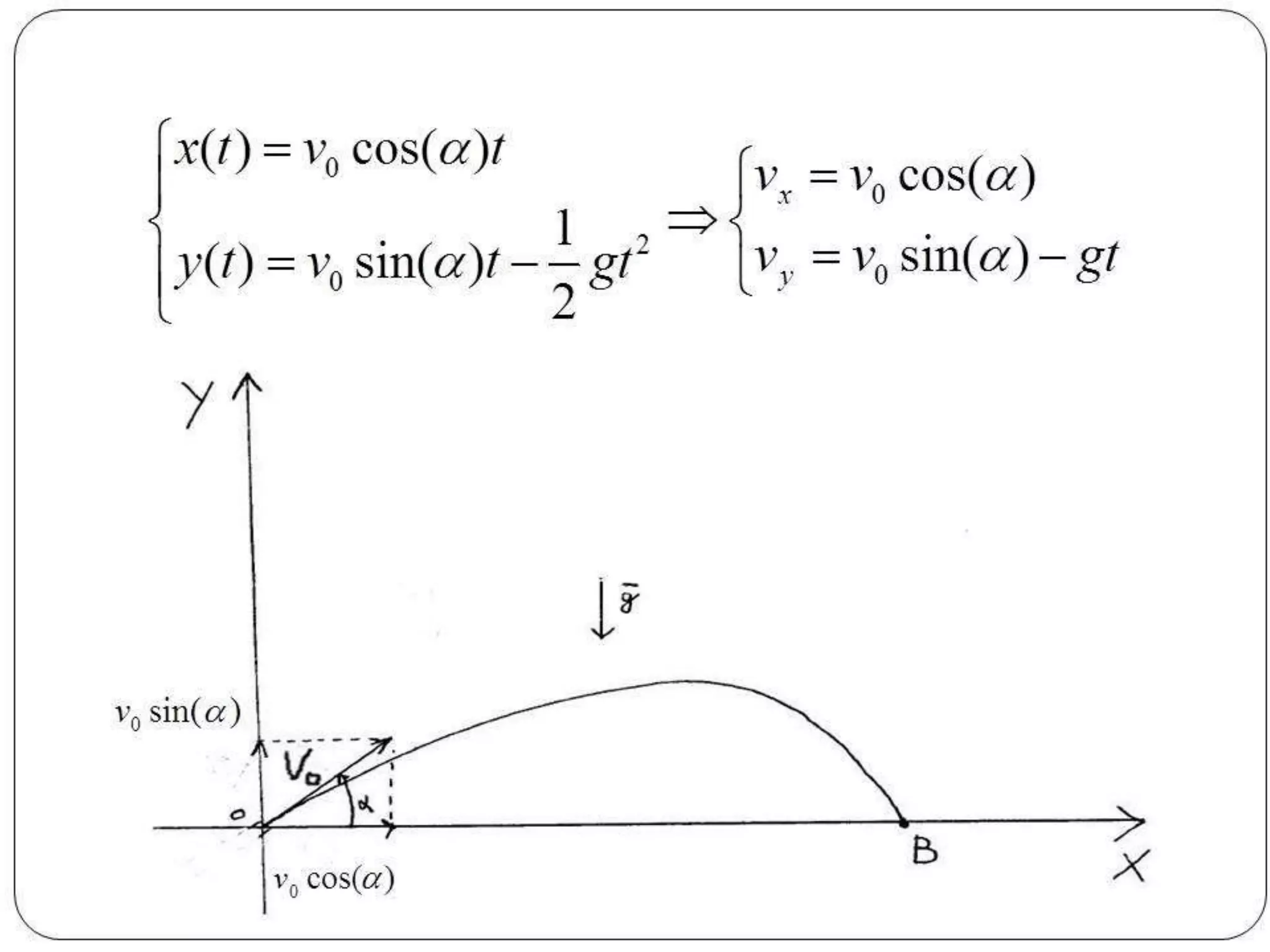
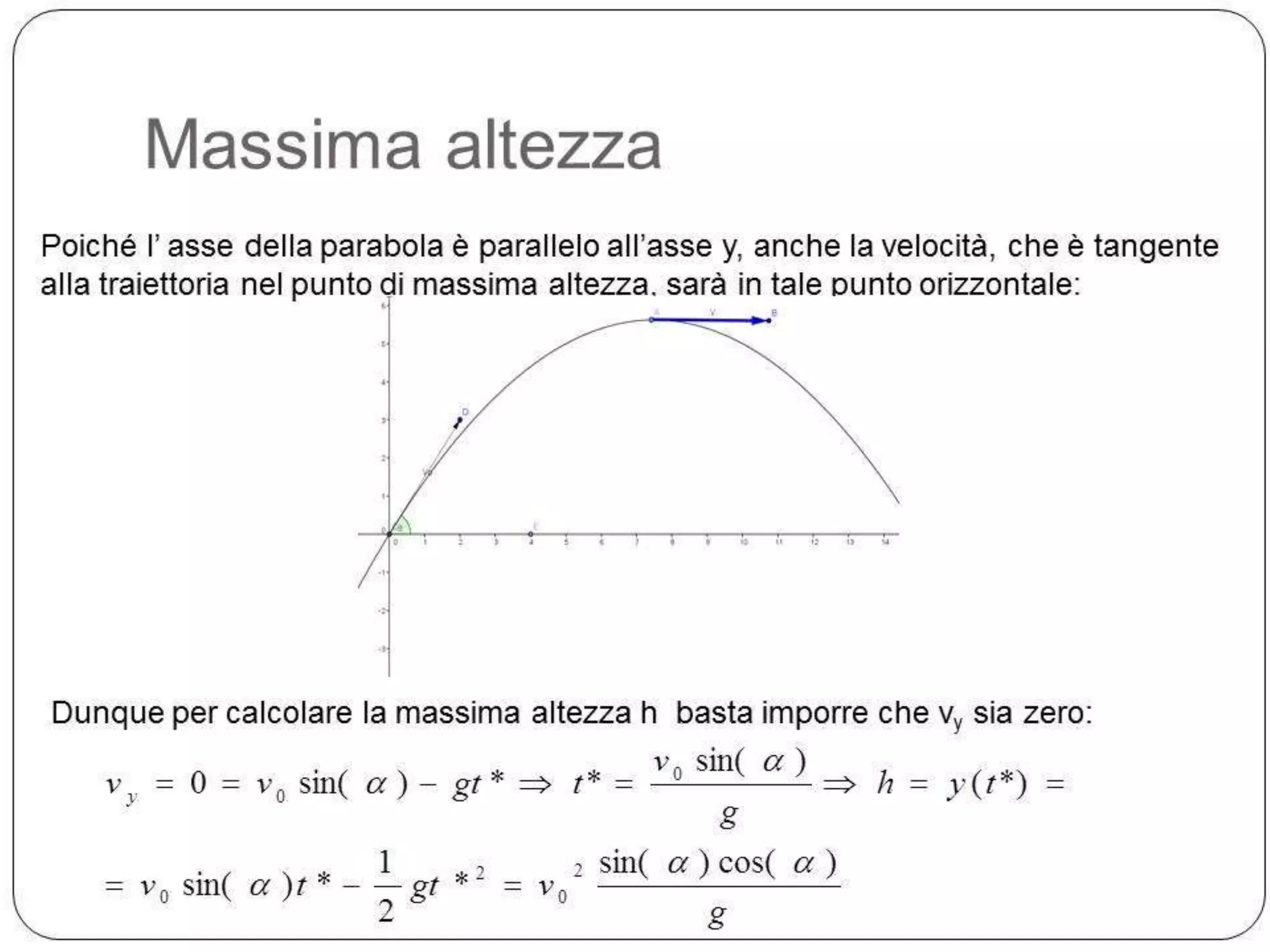
Il documento tratta del moto di un grave soggetto all'accelerazione di gravità di 9,8 m/s² e delle leggi del moto parabolico per un proiettile. Viene spiegato come calcolare la posizione e la velocità in funzione del tempo, utilizzando le componenti cartesiane per risolvere le equazioni del moto. Infine, viene indicato un link per esercizi pratici da svolgere.

1. MOTI ACCELERATI
PROF. ROMANO

2. Moto di un grave(1)
 E’ sperimentalmente provato che un grave in moto
lungo un asse verticale ha un’accelerazione di modulo
g = 9,8 m/s2 e diretta verso il basso. Se fissiamo un
asse z lungo la direzione di moto come in figura e
supponiamo z(0) = z0 abbiamo a = -g e quindi:
z (t )
v(t )
z0
v0t
v0
gt
1 2
gt
2
asse z
Z0
O

3. Un esempio
 Supponiamo di lasciar cadere un corpo da un’ altezza
z0. Poiché la velocità iniziale è nulla, la legge del moto
è:
z (t )
v(t )
1 2
z0
gt
2
gt 0
Il corpo arriva al suolo all’ istante t* tale che z(t*) =
0. Si ricava :
0
z0
v
1
g (t*)2
2
2 gz0
t*
2 z0
g
v(t*)
gt*
g
2 z0
g

4. Somma in coordinate cartesiane
 Se due vettori del piano u e v hanno rispettivamente
componenti (ux,uy) e (vx,vy), possiamo scrivere:
u = uxi + juy
v = vxi + jvy
essendo i e j i versori (vettori di modulo uno) degli assi.
u +v = (ux + vx)i+(uy + vy)j

5. Ogni vettore può essere scomposto nelle sue componenti
cartesiane secondo lo schema seguente:

6. Accelerazione vettoriale
Esattamente come si fa per la velocità, è possibile definire una accelerazione
media con la posizione:
Nel caso del moto di un proiettile si dimostra che l’accelerazione vettoriale
vale am = g con g diretta verso il basso e di modulo |g| = 9,8 m/s2 :
g

7. Moto di un grave(2) (proiettile)
Da quanto detto possiamo scrivere la relazione generale per Il moto parabolico:
R(t) = R0 + V0t + (1/2)gt2 1)
Se prendiamo un piano contenente sia g che V0 il moto avviene in questo piano e
quindi possiamo ridurci a solo due componenti. Quando si ha una relazione
vettoriale è possibile trasformarla in 2 equazioni tra numeri prendendo le
componenti dei due membri prima rispetto all’asse x e poi rispetto all’asse y.
Questa è una proprietà matematica che non dimostriamo. Dunque, del tutto in
generale, possiamo scrivere:
U
V
UX
VX ,U Y
VY
Il vettore R0 è il vettore posizione all’istante iniziale. Se il punto si trova per t = 0
all’origine degli assi, è R0 = 0 . Supponiamo inoltre che la velocità iniziale V0
formi con l’asse x un angolo α . La 1) da luogo alle due equazioni (scalari) :

8. x(t ) v0 cos( )t
1 2
y (t ) v0 sin( )t
gt
2
vx
v0 cos( )
vy
v0 sin( ) gt
v0 cos( )
v0 sin( )
v0 cos( )

9. Gittata del proiettile
Volendo trovare le coordinate del punto B del grafico, dobbiamo calcolare
l’istante t* in cui il proiettile, che parte da quota y = 0, si ritrova alla stessa
altezza. Calcolato t* dalla seconda equazione, lo inseriamo nella prima
per calcolare x(t*) = gittata:
1
0 y(t*) v0 sin( )t * g (t*)2
2
OB
v0 sin( )
v0 cos( )t* v0 cos( )2
g
0
t*
v0 sin( )
2
g
2
v sin( ) cos( )
2 0
g

10. Equazione della traiettoria
Se ricaviamo t dall’ equazione per x(t) e la sostituiamo in quella per y otteniamo
l’equazione della traiettoria:
t
x(t ) v0 cos( )t
1 2
y (t ) v0 sin( )t
gt
2
y
x
v0 cos( )
x
1
x
y v0 sin( )
g
v0 cos( ) 2 v0 cos( )
x2
xtg ( ) g
2
2v0 cos2 ( )
2

11. Massima altezza
Poiché l’ asse della parabola è parallelo all’asse y, anche la velocità, che è tangente
alla traiettoria nel punto di massima altezza, sarà in tale punto orizzontale:
Dunque per calcolare la massima altezza h basta imporre che vy sia zero:
vy
0
v0 sin( )
v0 sin( )t *
gt*
1
gt *2
2
v0 sin( )
g
sin( ) cos( )
g
t*
v0
2
h
y (t*)

12. Esercizi per casa
Gli esercizi presi dal Walker volume uno sono scaricabili dal seguente link:
http://antromano74.altervista.org/3b/esercizi-cinematica-3B.pdf
Consigliati 1, 2, 4 a pagina 45 , 17 pagina 46, 21 e 24 pagina 47