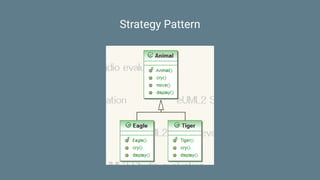
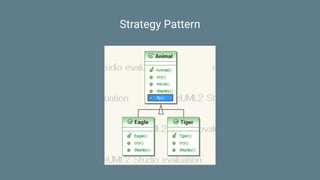
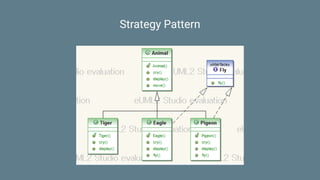
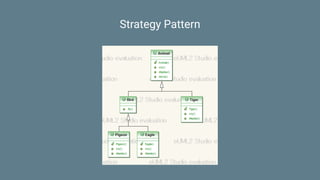
This document discusses functional programming concepts including SOLID design principles, strategy pattern, composition over inheritance, algebraic design, functors, monads, applicatives, and how monads can be used for railway oriented programming. It provides code examples for defining functors and monads in Scala as well as examples of type representations for monomorphism, epimorphism, and isomorphism.

1. Monad and Algebraic Design in
Functional Programming

2. SOLID Design Pattern Principles
• Single Responsibility Principle
• Open/Closed Principle
• Liskov Substitution Principle
• Interface Segregation Principle
• Dependency Inversion Principle

3. Strategy Pattern

4. Strategy Pattern

5. Strategy Pattern

6. Strategy Pattern

7. Composition over Inheritance
(in OOP)

8. Algebraic Design
if S (system of axioms) → then Q (set of theorems)

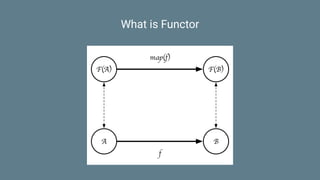
9. Functor
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)
def mapply[A, B](a: A)(f: F[A => B]): F[B] = map(f)((ff: A => B) => ff(a))
def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => (a, f(a)))
}
// Functor Law
// identity element
map(fa)(identity) == fa // must be true

10. What is Monad
Option, Either, List, Par, State and something like that...

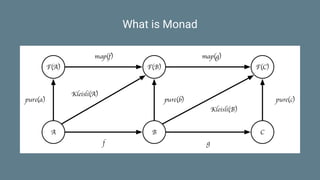
11. What is Monad: Part 1 - flatMap
trait Monad[F[_]] extends Functor[F] {
def pure[A](x: => A): F[A]
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
def map[A, B](fa: F[A])(f: A => B): F[B] = flatMap(fa)((a: A) => pure(f(a)))
}
// Monad Laws
// a. associated law
flatMap(flatMap(fa)(f))(g) == flatMap(fa)(b => flatMap(f(b))(g))
// b. identity element
flatMap(fa)(unit) == fa
flatMap(unit(a))(f) = f(a)

12. What is Monad: Part 2 - compose of Kleisli Arrow
type Kleisli[F[_], A, B] = A => F[B]
trait Monad[F[_]] extends Functor[F] {
def pure[A](x: => A): F[A]
def compose[A, B](k1: Kleisli[F, A, B], k2: Kleisli[F, B, C]): Kleisli[F, A, C]
// def compose(k1: A => F[B], k2: B => F[C]): A => F[C]
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] = compose(() => fa, f)
}
// Monad Laws
// a. associated law
compose(compose(f, g), h) == compose(f, compose(g, h))
// b. identity element
compose(f, pure) == f
compose(pure, f) == f

13. What is Monad: by definition
• pure & flatMap or pure & compose
• associated law and identity elements

14. What is Functor

15. What is Applicative

16. What is Monad

17. Why Monad
A monad is a control mechanism for sequencing computations

18. Why Monad: Railway Oriented Programming
def validate(a: A): Either[Exception, A] = ???
def update(a: A): Either[Exception, B] = ???
def send(b: B): Either[Exception, Response] = ???
val resE: Either[Exception, Response] = for {
va <- validate(a)
b <- update(va)
res <- send(b)
} yield res

19. Sample: Type Representation of Monomorphism &
Epimorphism
type Mon[A, B] = Kleisli[Some, A, B]
type Epi[A, B] = Kleisli[Option, A, B]

20. Isomorphism
type Iso[A, B] = A => B

21. Monomorphism
type Mon[A, B] = Kleisli[Some, A, B]

22. Epimorphism
type Epi[A, B] = Kleisli[Option, A, B]