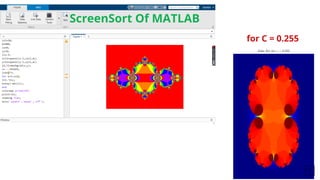
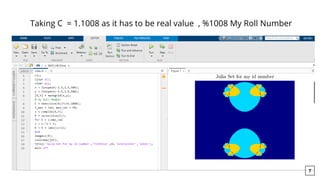
The document discusses the implementation of Julia sets using MATLAB, specifically for various complex numbers. It describes the process of generating fractals by iterating a complex function and provides sample code to visualize the Julia set for specific values of c. The document also mentions the connection to the Mandelbrot set and encourages experimentation with different parameters to create diverse graphics.

1. Implementation of
Julia Set

2. 1
2
3
Topics
For c = - 0 . 745429
For c = +1 . 1008 // My Id 1008
Graph for Different C
For C = 0.255
Different Julia Set as Per MAndelbrot Set .
About Julia Set
Introduction
MATLAB Code
Different graphs
2

3. 3
INTRODUCTION TO JULIA SET
Julia set fractals are normally generated by initializing a complex
number z = x + yi where i2 = -1 and x and y are image pixel coordinates
in the range of about -2 to 2. Then, z is repeatedly updated using:
f(z) = z² + c where c is another complex number that gives a specific
Julia set. After numerous iterations, if the magnitude of z is less than
2 we say that pixel is in the Julia set and color it accordingly.
Performing this calculation for a whole grid of pixels gives a fractal
image.

4. Que .)
Write a program using MATLAB to find the filled in Julia sets for the
function of the form f(z) = z^2 +c. For different real values of c.
10
% Implementing Julia Set in MATLAB for C = -0.74529
%For Random C
% here clearing command window and workspace
clc;
close all;
% here initialising initial values
col=30;
m=400;
cx=0;
cy=0;
l=1.5;
% As linspace will generate the vector for x and y as it will give linerly
% spacing between the points which help a lot in plotting at every point in
% the complex plane
x=linspace(cx-l,cx+l,m); 4

5. % using meshgrid to convert out vector x and y into array for plotting
% purpose
[X,Y]=meshgrid(x,y);
% initialising C as it was asked for real value of c
c= -.745429;
% Initialising the Z complex variable as i in term of x and y .
Z=X+1i*Y;
% Iterates till col = 30
for k=1:col;
Z =Z.^2+c;
% finding absolute value of the complex variable for the c
W=exp(-abs(Z));
end
% using colormap to give colour to the graph as it was required for
% colourful images
colormap prism(415)
% pcolor because it create a colourful pseudo plot what we wanted;
pcolor(W);
5

6. % shading sets the EdgeColor and FaceColor properties to flat to picture it
% more nice .
shading flat;
% give title to the graph ,
title('Julia Set for $c=-0.74529$','FontSize',16,'interpreter','latex');
% provide axis details
axis('square','equal','off');
% we can change the value of c in the code to get different graph
6

7. ScreenSort Of MATLAB
for C = 0.255
7

8. 7
Taking C = 1.1008 as it has to be real value , %1008 My Roll Number

9. MandelBrot has Fixed Image :
Fot that We can take different
value of C from mandelbrot
set and can see what actual
graph for the Corresponding
Julia Set .
8

10. We can also see very different and beautiful graph for complex value of c .
For example :-
9

11. 3D Julia set
10

12. THANK
YOU !
Reference : MATLAB ,
Wikipedia
My Code : Matlab
11