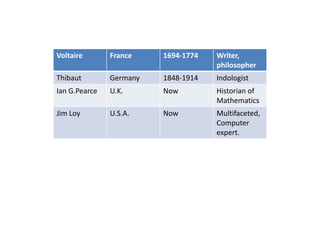
This document discusses the presence of the Pythagorean theorem in ancient Sanskrit texts that predate Pythagoras. It provides quotes and passages from several Sanskrit works including the Sulvasutras, Aryabhateeyam, Brahmasphutasiddhanta, Trishatika, and Lilavati that describe or prove the Pythagorean theorem. The document also notes that scholars like Thibaut, Pearce, and Loy have acknowledged the theorem's early description in Indian mathematics texts, with some versions possibly dating back to 800 BCE.

1. Modern Mathematics in old Sanskrit
books
Module 4
Pythagoras Theorem

2. Three Parts
• Part 1: Four Quotes.
• Part 2: Five Sanskrit passages.
• Part 3: Six remarks.

3. Pythagoras formula
In a triangle ABC, if the
angle at B is a right
angle, then AC2 = AB2 +
BC2.
• If c is the largest side in
a right angled triangle,
and if a and b are the
other two sides, then c2
= a2 + b2.
A
B C

4. Pythagoras
• Pythagoras of Samos
was a Greek
philosopher,
mathematician and
founder of a religious
movement called
Pythagoreanism.

5. Quote
• “I am convinced that
everything has come
down to us from the
banks of
Ganga(Ganges), -
Astronomy, Astrology,
metempsychosis,etc.”

6. William Thibaut
George Frederick William Thibaut
(March 20, 1848–1914) was an
Indologist notable for his
contributions to the understanding
of ancient Indian mathematics and
astronomy.
Thibaut was born in Germany,
worked briefly in England, and then
in 1875 was appointed Professor at
the Government Sanskrit College ,
Varanasi

7. Quote
The geometrical theorem I-47 of Sulba sutra
which tradition ascribes to Pythagoras, was
solved by Hindus atleast two centuries earlier.
- Dr. Thibaut,
Jour.Asiatic society of Bengal
(1875),p.227.

8. Quote
• “Many of the vedic contributions to
mathematics have been neglected or worse.
When it first became apparent that there was
geometry contained within works that were
not of Greek origin, historians and
mathematical commentators went to great
length to try and claim that this geometry was
Greek-influenced.”
--Ian G.Pearce.

9. Jim Loy
• One of the most visited sites on the internet.
• “The proof by Legendre was probably
originally devised by an ancient Hindu
mathematician”.

10. Voltaire France 1694-1774 Writer,
philosopher
Thibaut Germany 1848-1914 Indologist
Ian G.Pearce U.K. Now Historian of
Mathematics
Jim Loy U.S.A. Now Multifaceted,
Computer
expert.

11. Part 1 ends.
Part 2 starts.

12. Names of this theorem
• Bhuja koti karna nyaya
• Hypotenuse theorem
• Diagonal square theorem
• Sulva theorem
• Bodhayana theorem.

13. Five Sanskrit books
• Sulvasutra (of Bodhaayana and of Apastamba)
• Aryabhateeyam (of Aryabhata)
• Brahmasphutasiddhanta (of Brahmagupta)
• Trishatika (of Sridhara)
• Lilavati (of Bhaskara)

14. This is a statement in Chapter I of Bodhaayana’s
Sulvasutra.
Deergha chaturasrasya akshnayaa rajjuh
paarshvamaanee tiryangmaanee cha
yat pruthagbhuute kurutah tat ubhayam karoti

15. Source Book

16. Translation: In a rectangle, the square of the
diagonal is equal to the sum of the squares of
the adjacent sides.
Technical terms:
Dirgha caturasra = rectangle.
Akshnayaa = along the diagonal.
Parshvam &tiryak = two adjacent sides.
Karoti = yields a square.

17. Usages of the word akshnaya
(this word seems to be available only
in vedic literature.)word meaning book
akshnayavan One who goes transversely Rigveda
akshnaya 1.Across 2.in a crooked way Satapata Brahmanam
Akshnayadesam Interim region --do--
Akshnayaapaccedanam Cutting across Sulvasutra
akshnayaastomeeya Name of something Taittiriya samhita

18. Quote
• “This (passage from Sulbasutra) appears to be
referring to a rectangle, although some
interpretations consider this to refer to a
square. … The text seems to be quite open to
unequal sides. If this refers to a rectangle, it is
the earliest recorded statement of the
Pythagorean theorem”. – Wikipedia.

19. Quote
• “Sulba sutras include unarguable evidence of
the use of Pythagoras theorem and
Pythagorean triples, predating Pythagoras
(c.572-497B.C.) and evidence of a number of
geometrical proofs”. – Ian G.Pearce., May
2002.

20. Aryabhateeyam
•
Whatever is the square of
the base and the square
of the perpendicular
side, that (together) is
the square of the
hypotenuse.

21. From Brahma gupta’s work
•
• Hypotenuse is the square root of the sum of
the squares of the base and the perpendicular
side.
• C = √(a^2+b^2)
-- Brahma sphuta siddhanta.

22. Sridhara
•
Take the two quantities namely base and the
perpendicular side. Square them and add.
Take the square root. It becomes the length of
the hypotenuse.
-- Trisatika.

23. Bhaskara
•
•
Given a side, the other side perpendicular to it is
called koti. This terminology applies to both the
triangles and quadrilaterals. The square root of
the sum of the squares of these two is the
hypotenuse.
-Lilavati, kshetra vyavahara.

24. A page from Lilavati describing
Pythagoras theorem.

25. Time
• Bodhayana
• Aryabhata
• Brahmagupta
• Sridhara
• Bhaskara
• 800B.C.
• 476A.D.
• 628A.D.
• 8th century A.D.
• 1114A.D.

26. Six remarks
• Pythagoras theorem is very important. It is the first
among “the seventeen equations that changed the
world”.
• It is probably the only theorem having more than 200
proofs.
• Some proofs are available in Sanskrit books. One of the
oldest proofs is due to Bhaskara.
• Visit of Pythagoras to India is a controversial topic.
• Dating of Sulvasutras is a rich topic of investigation.
• Pythagorean triples form an interesting related topic.