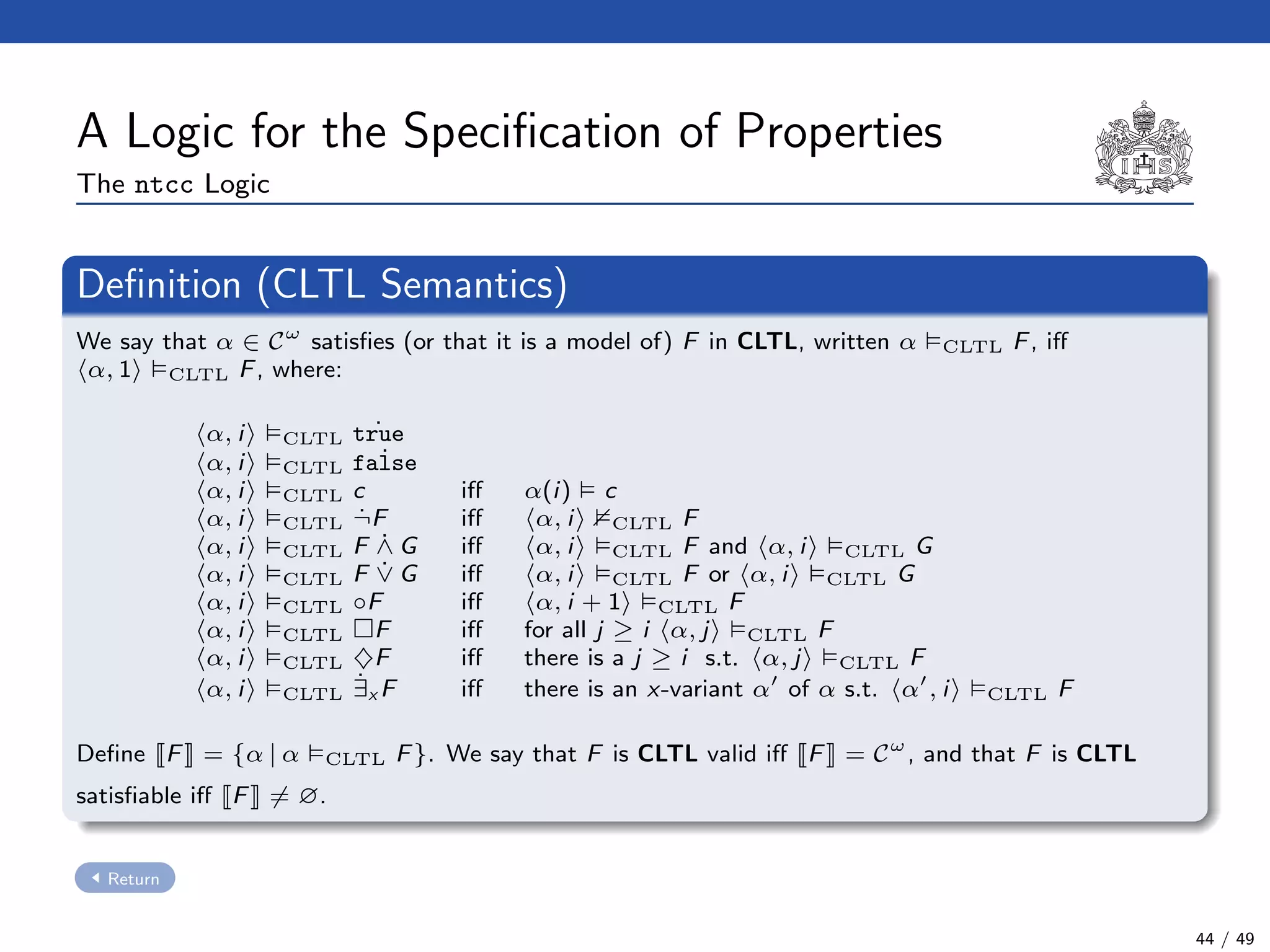
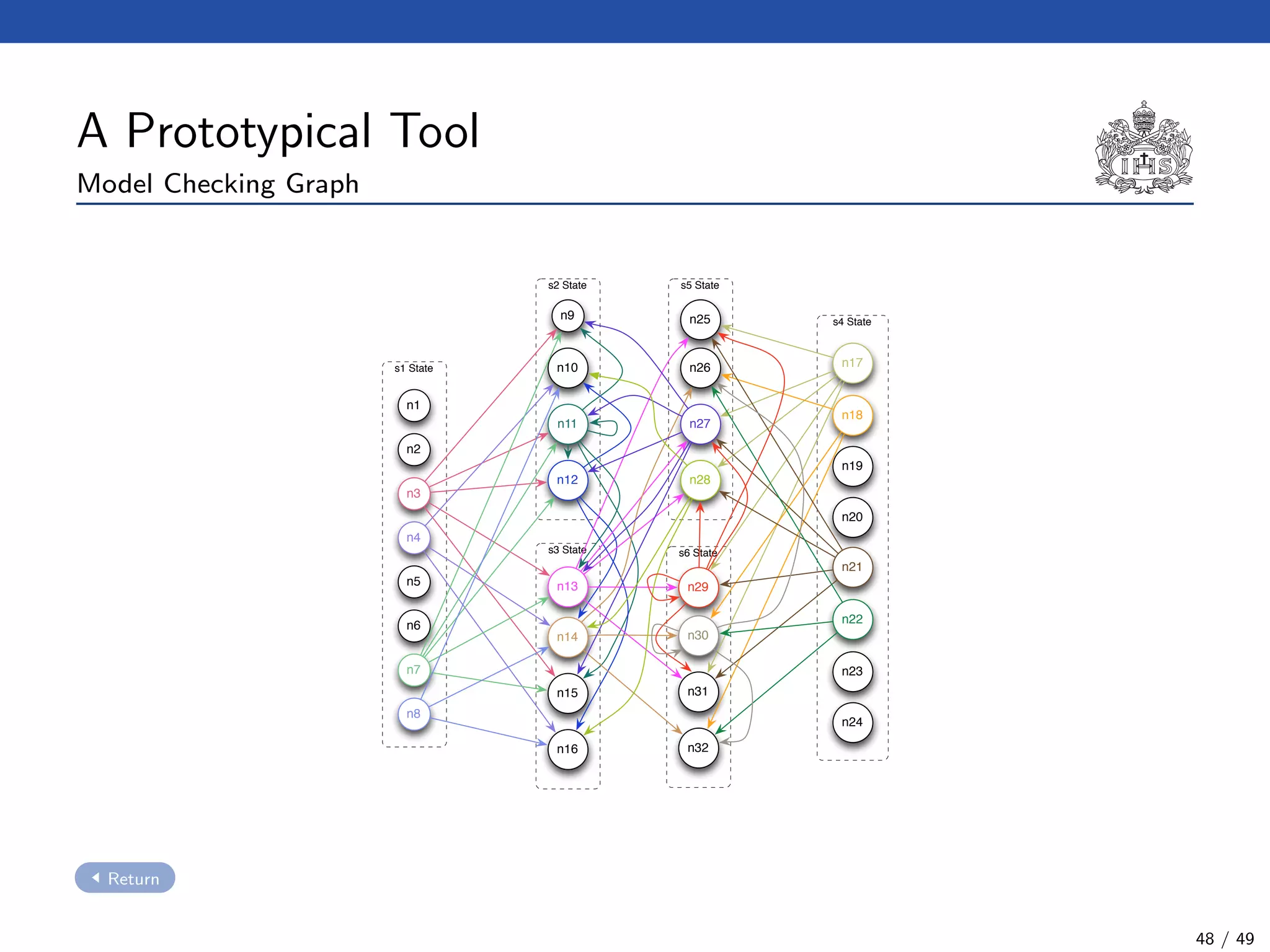
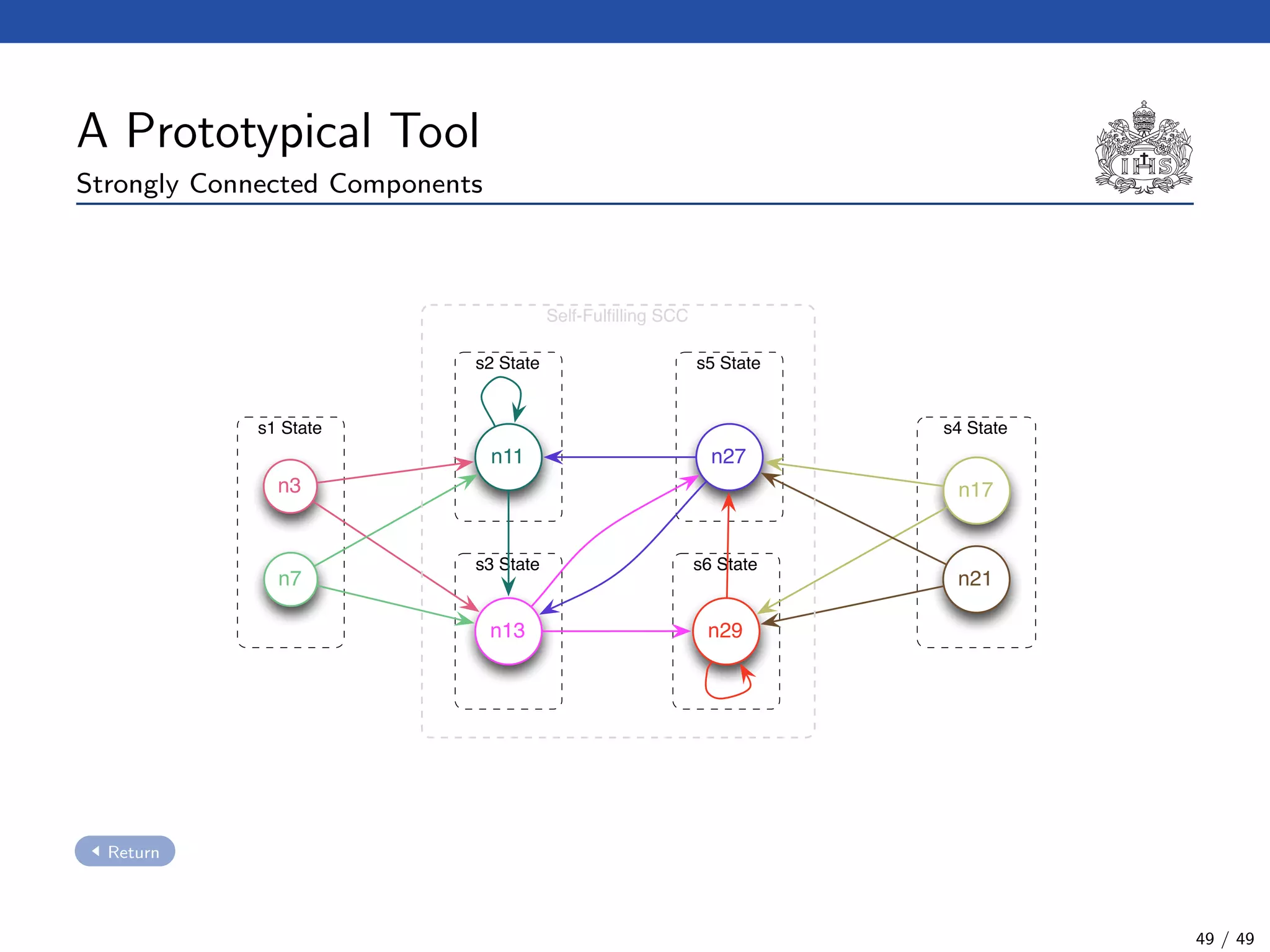
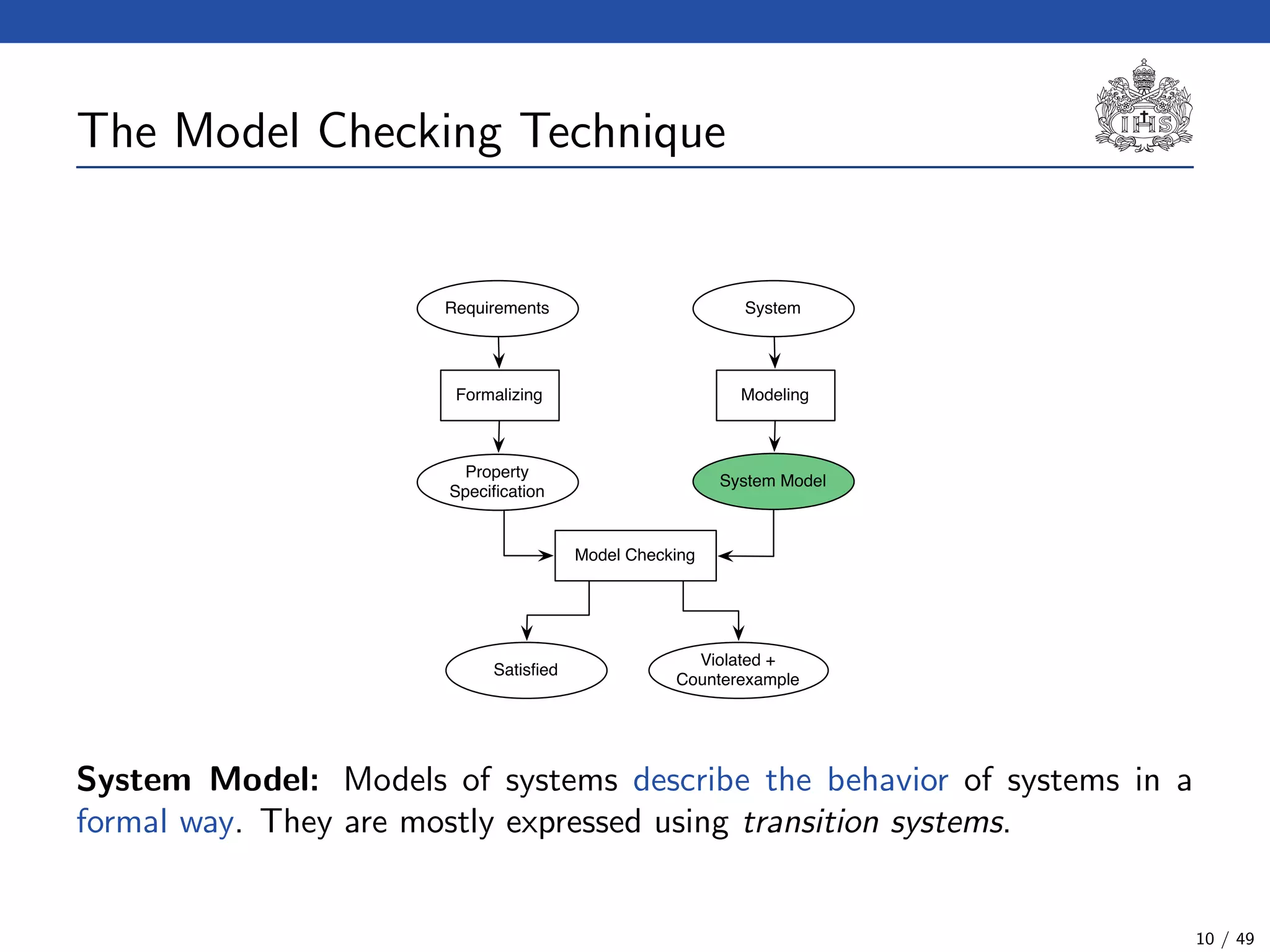
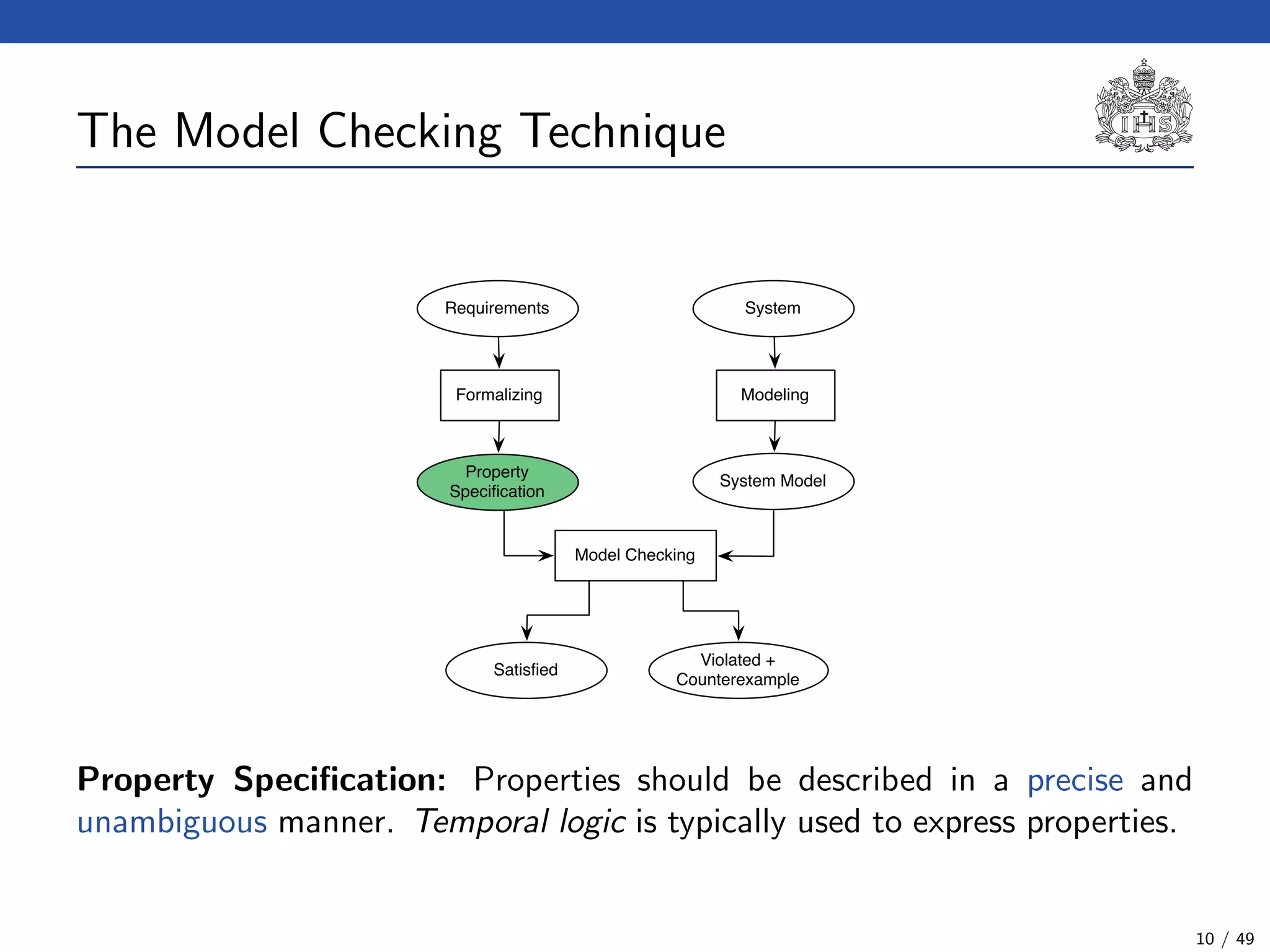
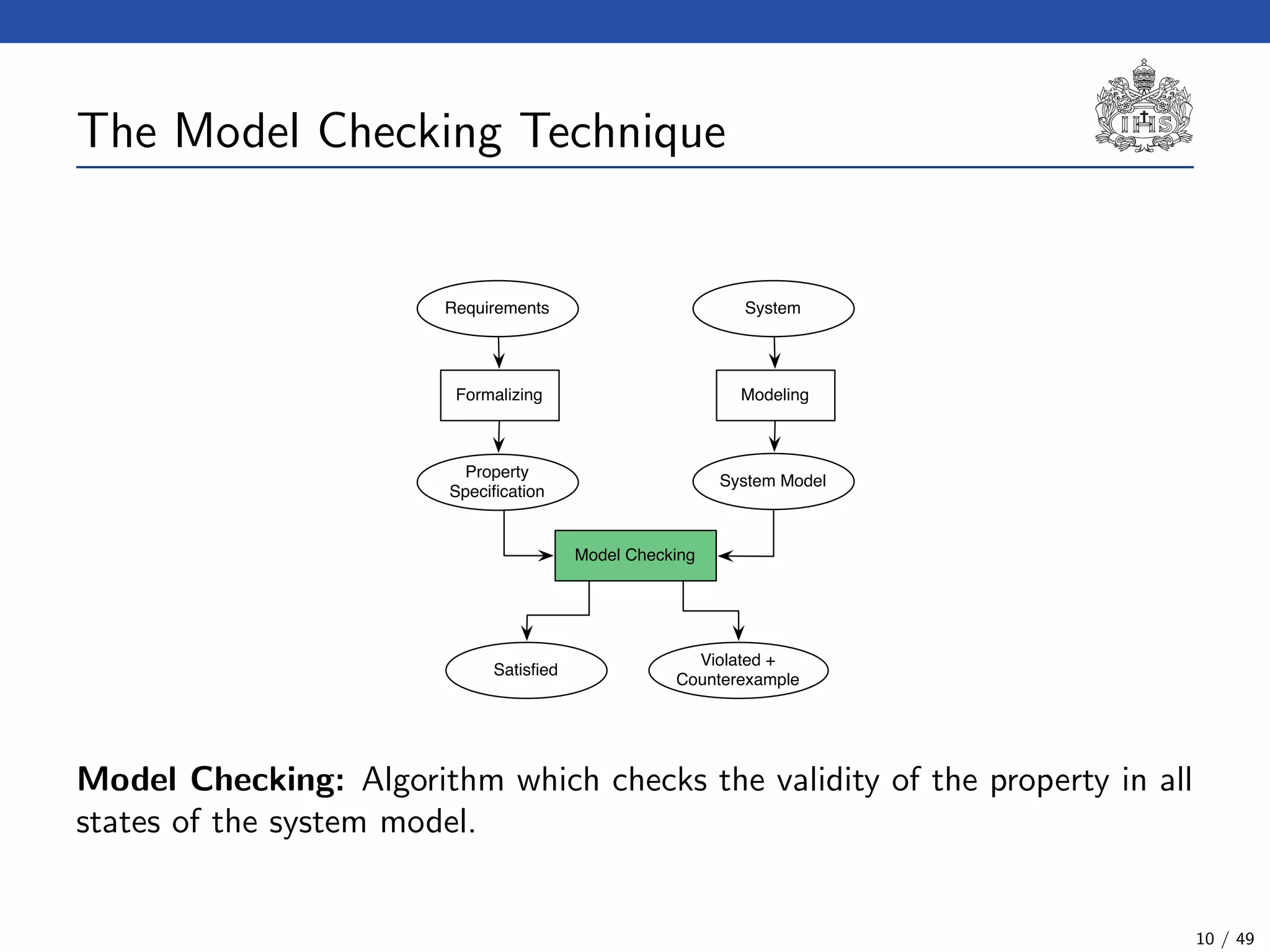
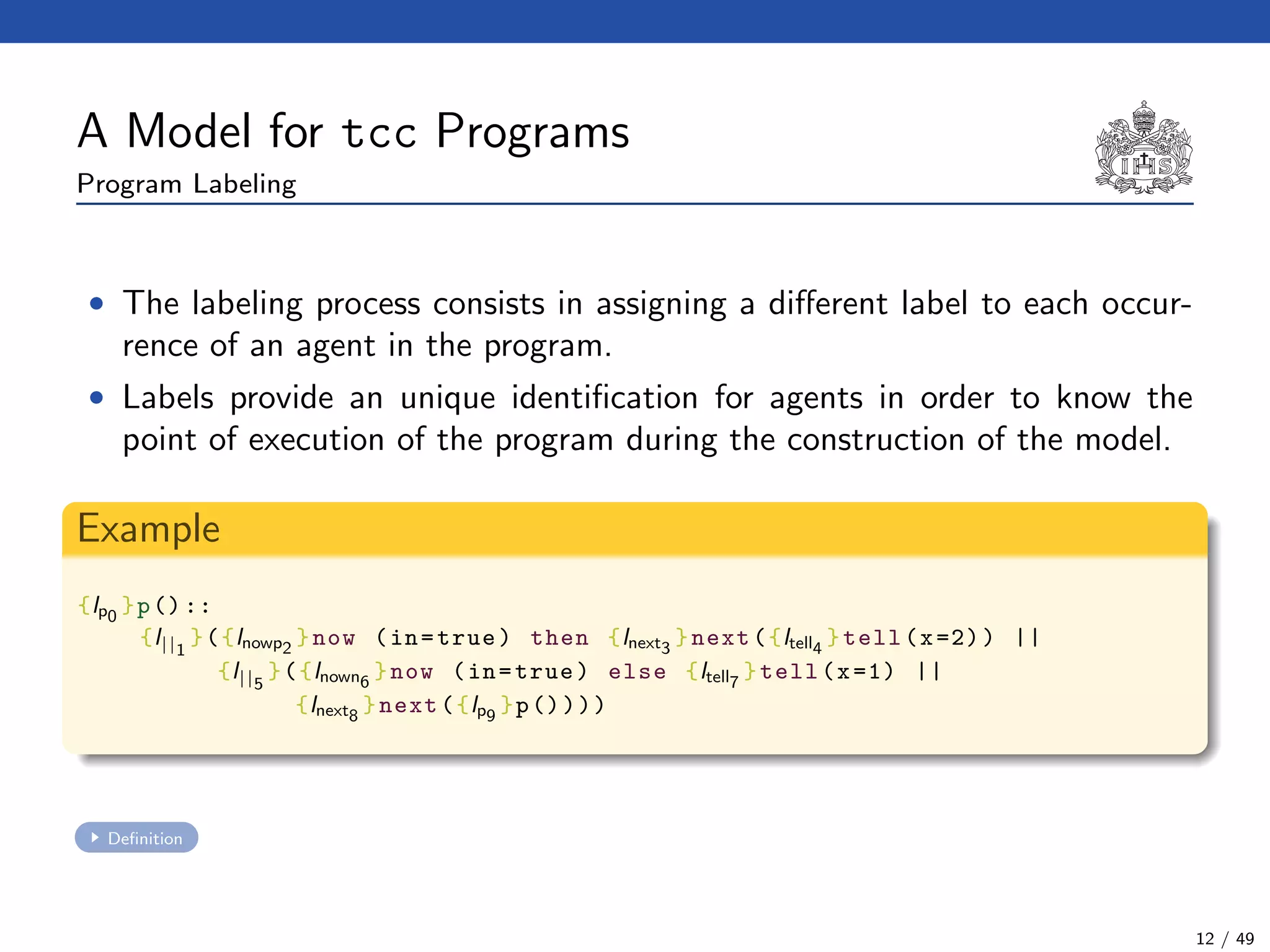
The document describes a model checking technique for the ntcc calculus. It involves constructing a tcc structure model from ntcc programs by labeling occurrences of agents. The tcc structure is a variant of a Kripke structure that models the behavior of ntcc specifications. Properties are formally specified using temporal logic. The model checking algorithm then checks if the tcc structure model satisfies the temporal logic properties.

1. ntccKMC: A Kripke-structure-based model checker for the
ntcc calculus
Cali
Mauricio Toro Bermudez,
in joint work with Jaime Arias,
Carlos Olarte and Camilo Rueda
AVISPA Research Group
Pontificia Universidad Javeriana - Cali
February, 2013

2. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
2 / 49

3. Motivation
• Verification of ntcc programs is performed using inductive techniques since
the model does not provide automatic formal verification tools.
• Problems:
◦ Difficult
◦ Error prone
◦ Experts are required.
• Hubert Garavel [Gar08]: “...The research agenda for theoretical concur-
rency should therefore address the design of efficient algorithms for trans-
lating and verifying formal specifications of concurrent systems”.
3 / 49

4. Motivation
• Model checking is an automated technique that, given a finite-state model
of a system and a formal property, systematically checks whether this
property holds for (a given state in) that model [CGP99].
• Advantages
◦ Formal technique.
◦ Fully-automatic.
◦ Experts are not required.
◦ Counterexample.
• Drawback
◦ State-space explosion problem.
4 / 49

5. React-PLUS project
• REACT PLUS addresses the development and application of formal
methods in real-life systems.
• It takes the challenging task of developing the underlying theory and
machine-assisted tools for verifying concurrent systems specified in a
formalism AVISPA has recently developed, the ntcc calculus.
5 / 49

6. The problem
• At present, ntcc does not provide for the automatic, or even
machine-assisted, verification of system properties.
• Since we deal with complex and large systems, machine-assisted
verification is essential to our intended applications.
6 / 49

7. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
7 / 49

8. Previous work
1. Given a ntcc process and a CLTL property, transform the process into a
B¨uchi automaton and the formula into a process [Val05].
8 / 49

9. Previous work
1. Given a ntcc process and a CLTL property, transform the process into a
B¨uchi automaton and the formula into a process [Val05].
2. Given a tccp process, a temporal logic property and a number n of time
units, generate a kripke structure and verify if the property satisfy such
structure [FV06].
8 / 49

10. Previous work
1. Given a ntcc process and a CLTL property, transform the process into a
B¨uchi automaton and the formula into a process [Val05].
2. Given a tccp process, a temporal logic property and a number n of time
units, generate a kripke structure and verify if the property satisfy such
structure [FV06].
3. Given a probabilistic ntcc process, a probabilistic CTL property and
sequence of n inputs (i.e., constraints), generate a discrete-time markov
chain, export the chain into PRISM model checker and verify the
property [TB09]. http://ntccrt.sourceforge.net
8 / 49

11. Previous work
1. Given a ntcc process and a CLTL property, transform the process into a
B¨uchi automaton and the formula into a process [Val05].
2. Given a tccp process, a temporal logic property and a number n of time
units, generate a kripke structure and verify if the property satisfy such
structure [FV06].
3. Given a probabilistic ntcc process, a probabilistic CTL property and
sequence of n inputs (i.e., constraints), generate a discrete-time markov
chain, export the chain into PRISM model checker and verify the
property [TB09]. http://ntccrt.sourceforge.net
4. Given a ntcc process, a CLTL property and a number n of time units,
generate a finite-state automaton that represents the process and another
one that represents the property, then verify if the process satisfies the
formula [TB12]. http://ntccmc.sourceforge.net
8 / 49

12. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
9 / 49

13. The Model Checking Technique
Requirements System
Formalizing Modeling
Property
Specification
System Model
Model Checking
Satisfied
Violated +
Counterexample
System Model: Models of systems describe the behavior of systems in a
formal way. They are mostly expressed using transition systems.
10 / 49

14. The Model Checking Technique
Requirements System
Formalizing Modeling
Property
Specification
System Model
Model Checking
Satisfied
Violated +
Counterexample
Property Specification: Properties should be described in a precise and
unambiguous manner. Temporal logic is typically used to express properties.
10 / 49

15. The Model Checking Technique
Requirements System
Formalizing Modeling
Property
Specification
System Model
Model Checking
Satisfied
Violated +
Counterexample
Model Checking: Algorithm which checks the validity of the property in all
states of the system model.
10 / 49

16. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
11 / 49

17. A Model for tcc Programs
Program Labeling
• The labeling process consists in assigning a different label to each occur-
rence of an agent in the program.
• Labels provide an unique identification for agents in order to know the
point of execution of the program during the construction of the model.
Example
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) ||
{lnext8
}next({lp9
}p())))
Definition
12 / 49

18. A Model for tcc Programs
The tcc Structure
• tcc Structure is a graph structure which allows to model the behavior of
a tcc specification.
• It is a variant of a Kripke Structure.
current store
internal labels temporal labels
(a) tcc state
Internal Transition
Temporal Transition
(b) Transitions
Figure: Components of a tcc Structure
Definition
13 / 49

19. A Model for tcc Programs
Construction of the Model
Procedure Call:
p0
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

20. A Model for tcc Programs
Construction of the Model
Procedure Call:
p0
1
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

21. A Model for tcc Programs
Construction of the Model
Procedure Call:
p0
1
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

22. A Model for tcc Programs
Construction of the Model
Procedure Call:
p0
||1
1
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

23. A Model for tcc Programs
Construction of the Model
Parallel:
p0
||1
1
2
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

24. A Model for tcc Programs
Construction of the Model
Parallel:
p0
||1
1
2
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

25. A Model for tcc Programs
Construction of the Model
Parallel:
p0
||1
1
2
nowp2,
||5
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

26. A Model for tcc Programs
Construction of the Model
Parallel:
nowp2,
nown6,
next8
3
p0
||1
1
2
nowp2,
||5
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

27. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
3
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

28. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
3
4 19
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

29. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
3
4 19
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

30. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
in=true
3
4 19
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

31. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
~(in=true)in=true
3
4 19
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

32. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
~(in=true)in=true
3
4 19next3,
nown6,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

33. A Model for tcc Programs
Construction of the Model
Timed Positive Ask:
nowp2,
nown6,
next8
~(in=true)in=true
3
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

34. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

35. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
5 33
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

36. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
5 33
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

37. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5 33
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

38. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5
in=true,~(in=true)
33
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

39. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

40. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

41. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
34 20
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

42. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
34 20
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

43. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
34
~(in=true),in=true
20
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

44. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
34
~(in=true),in=true
20
~(in=true)
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

45. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
20
~(in=true)
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

46. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
20
~(in=true)
nowp2,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

47. A Model for tcc Programs
Construction of the Model
Timed Negative Ask:
~(in=true)in=true
4 19next3,
nown6,
next8
nowp2,
nown6,
next8
in=true
5next3,
next8
20
~(in=true)
nowp2,
next8
tell7
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

48. A Model for tcc Programs
Construction of the Model
Unit Delay:
5next3,
next8
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

49. A Model for tcc Programs
Construction of the Model
Unit Delay:
in=true
5next3,
next8
6
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

50. A Model for tcc Programs
Construction of the Model
Unit Delay:
in=true
5next3,
next8
6
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

51. A Model for tcc Programs
Construction of the Model
Unit Delay:
in=true
5next3,
next8
6
in=true
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

52. A Model for tcc Programs
Construction of the Model
Unit Delay:
in=true
5next3,
next8
6tell4,
p9
in=true
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

53. A Model for tcc Programs
Construction of the Model
Passage to the Next Time:
6tell4,
p9
in=true
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

54. A Model for tcc Programs
Construction of the Model
Passage to the Next Time:
6tell4,
p9
in=true
7
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

55. A Model for tcc Programs
Construction of the Model
Passage to the Next Time:
6tell4,
p9
in=true
7
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

56. A Model for tcc Programs
Construction of the Model
Passage to the Next Time:
6tell4,
p9
in=true
7tell4,
p9
{lp0
}p()::
{l||1
}({lnowp2
}now (in=true) then {lnext3
}next({ltell4
}tell(x=2)) ||
{l||5
}({lnown6
}now (in=true) else {ltell7
}tell(x=1) || {lnext8
}next({lp9
}p())))
14 / 49

57. A Model for tcc Programs
Construction of the Model
Equivalent States:
6tell4,
p9
in=true
7tell4,
p9
13tell4,
p9
x=2, in=true
14tell4,
p9
15 / 49

58. A Model for tcc Programs
Construction of the Model
Equivalent States:
6tell4,
p9
in=true
7tell4,
p9
13tell4,
p9
x=2, in=true
14tell4,
p9
15 / 49

59. A Model for tcc Programs
Construction of the Model
Equivalent States:
6tell4,
p9
in=true
7tell4,
p9
13tell4,
p9
x=2, in=true
15 / 49

60. A Model for tcc Programs
Construction of the Model
Equivalent States:
6tell4,
p9
in=true
7tell4,
p9
13tell4,
p9
x=2, in=true
• Reduction of states is necessary to decrease the state explosion problem.
• The store on the quiescent point is defined as the output of the
computation.
15 / 49

61. A Model for tcc Programs
Simplification of the Model
1 54
1 2 3 4 5
Sequence of internal transitions
(a) Reduction of a sequence of
internal transitions
2
1
3 4
2 2
1
3 4
(b) Reduction of a branching
Figure: Reduction rules
16 / 49

62. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
17 / 49

63. A Logic for the Specification of Properties
The ntcc Logic
• Linear temporal logic (LTL) named CLTL for reasoning about ntcc
processes.
• It expresses properties over sequences of constraints.
• ntcc is an extension of tcc.
Definition (CLTL Syntax)
The formulae F, G, . . . ∈ F are built from constraints c ∈ C in the
underlying constraint system by
F, G, . . . := c | ˙true | ˙false | F ˙∧ G | F ˙∨ G | ˙¬F | ˙∃x F | ◦ F | F | ♦F
Semantics
18 / 49

64. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
19 / 49

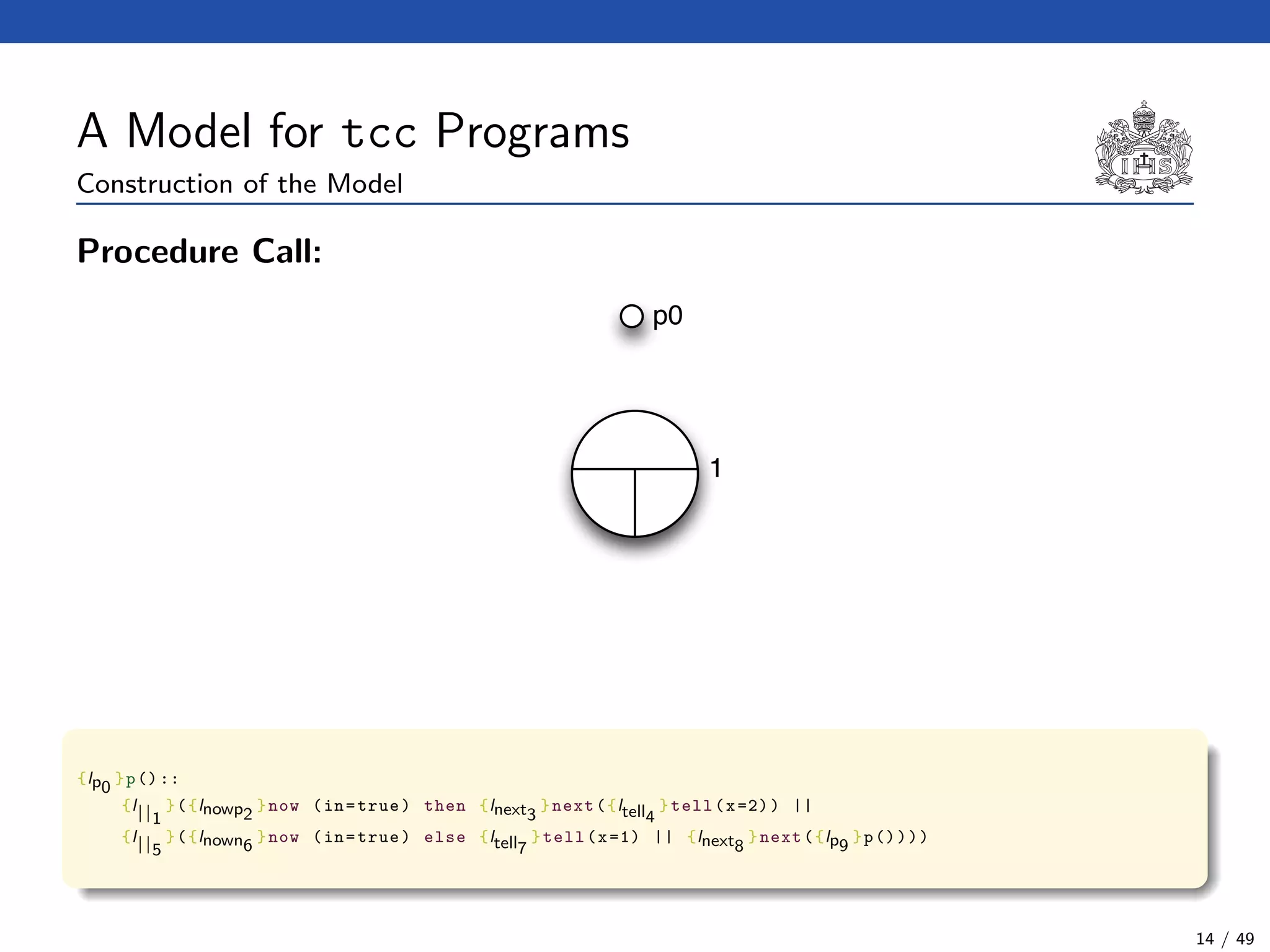
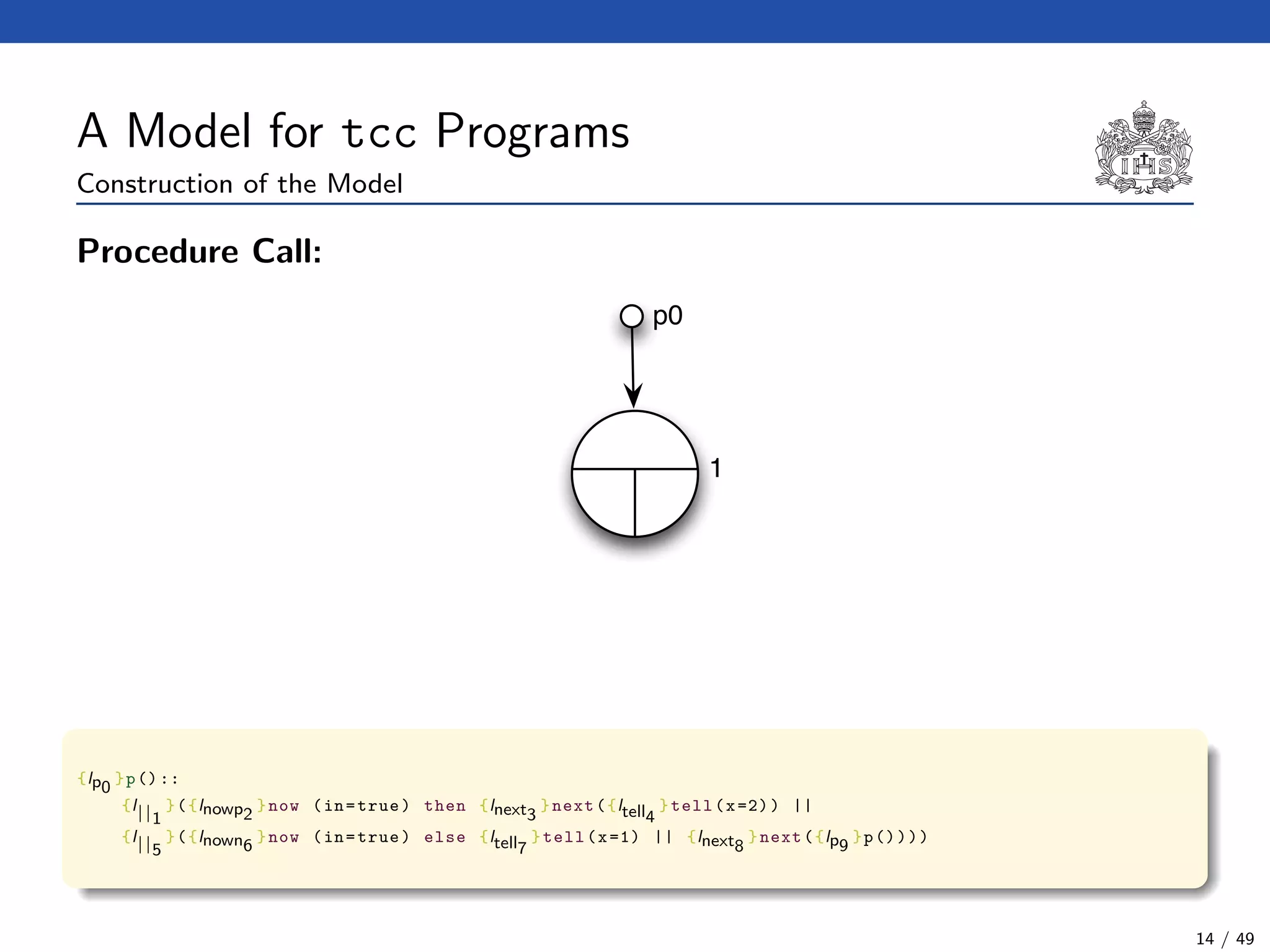
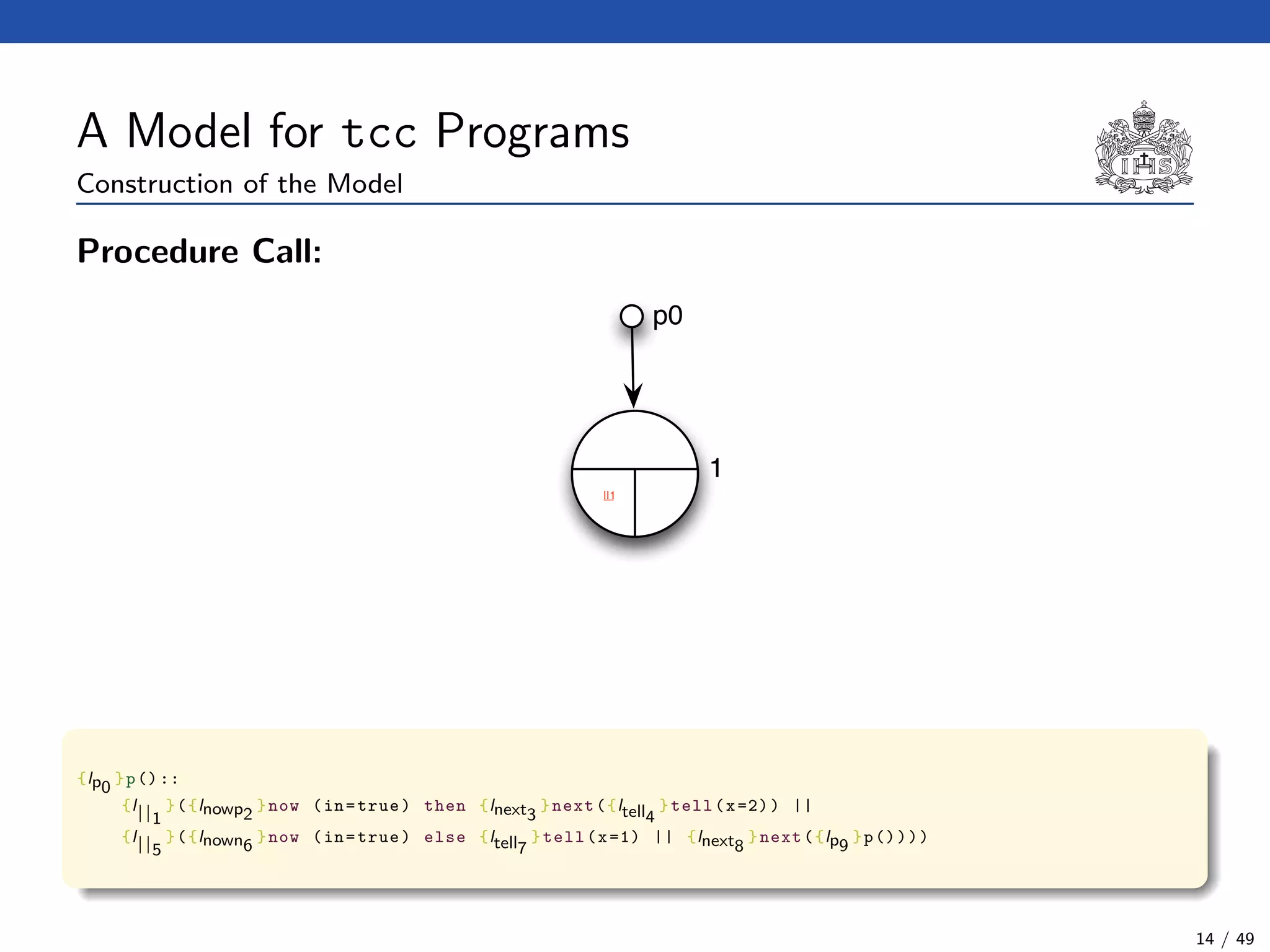
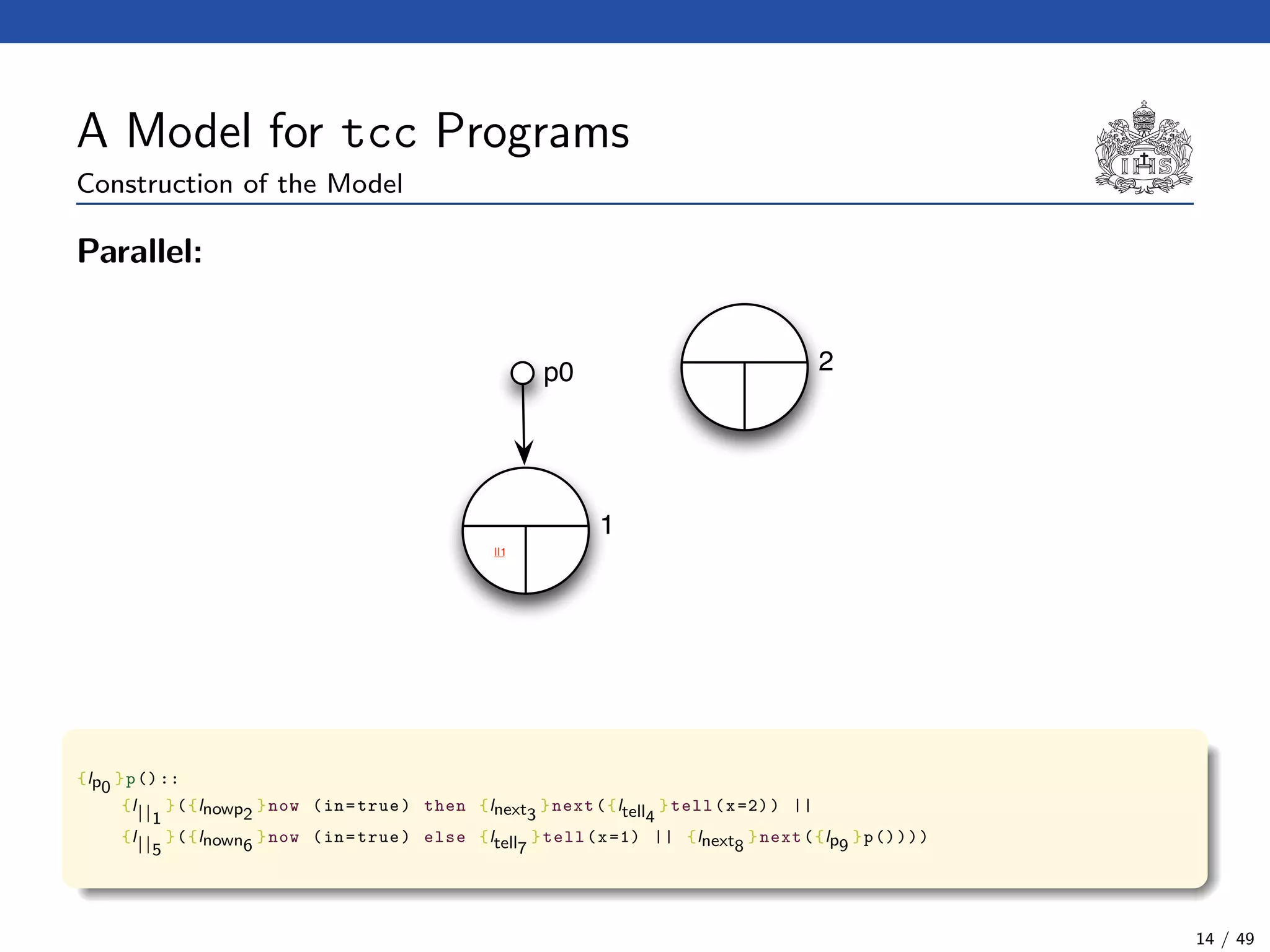
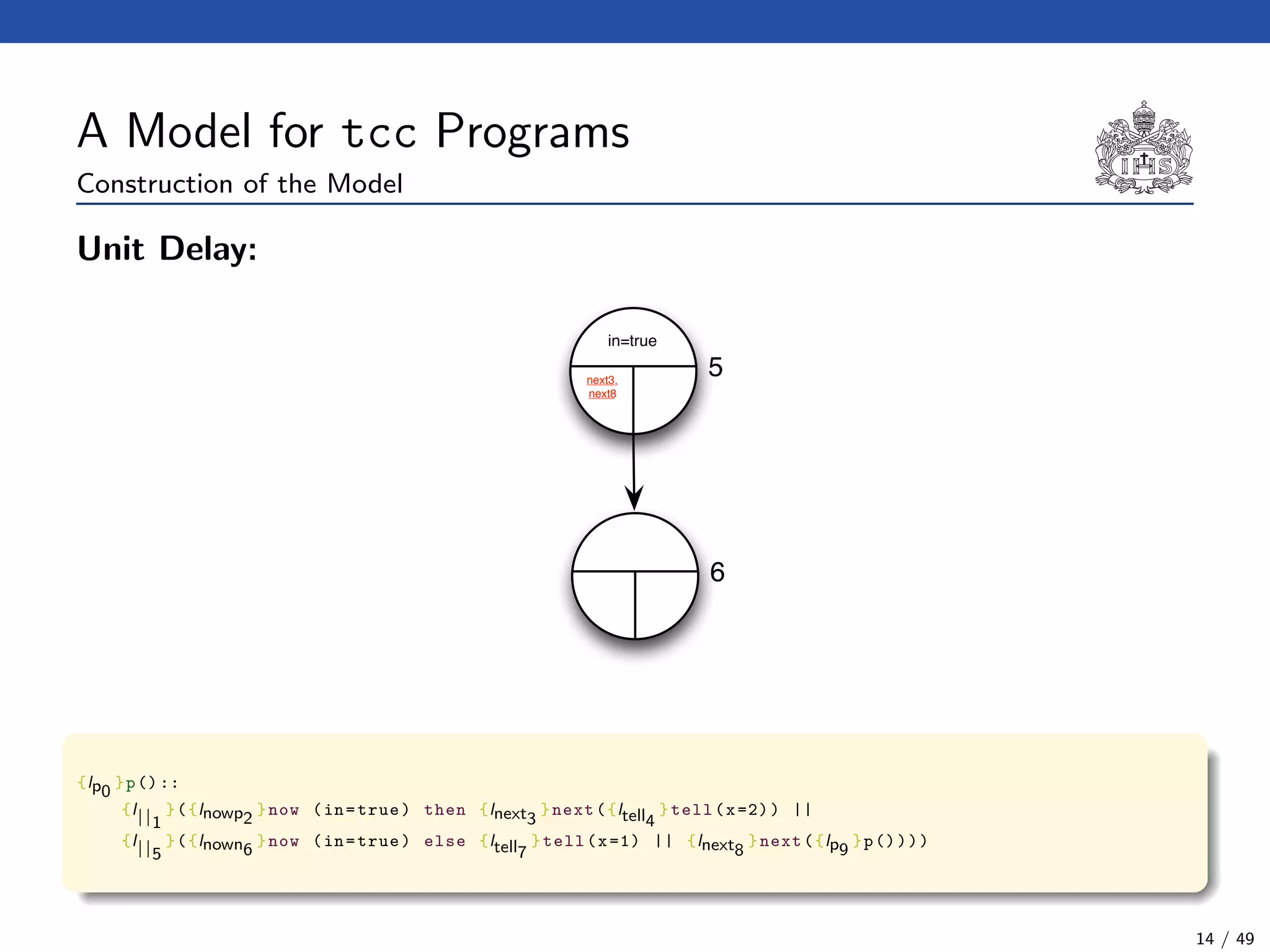
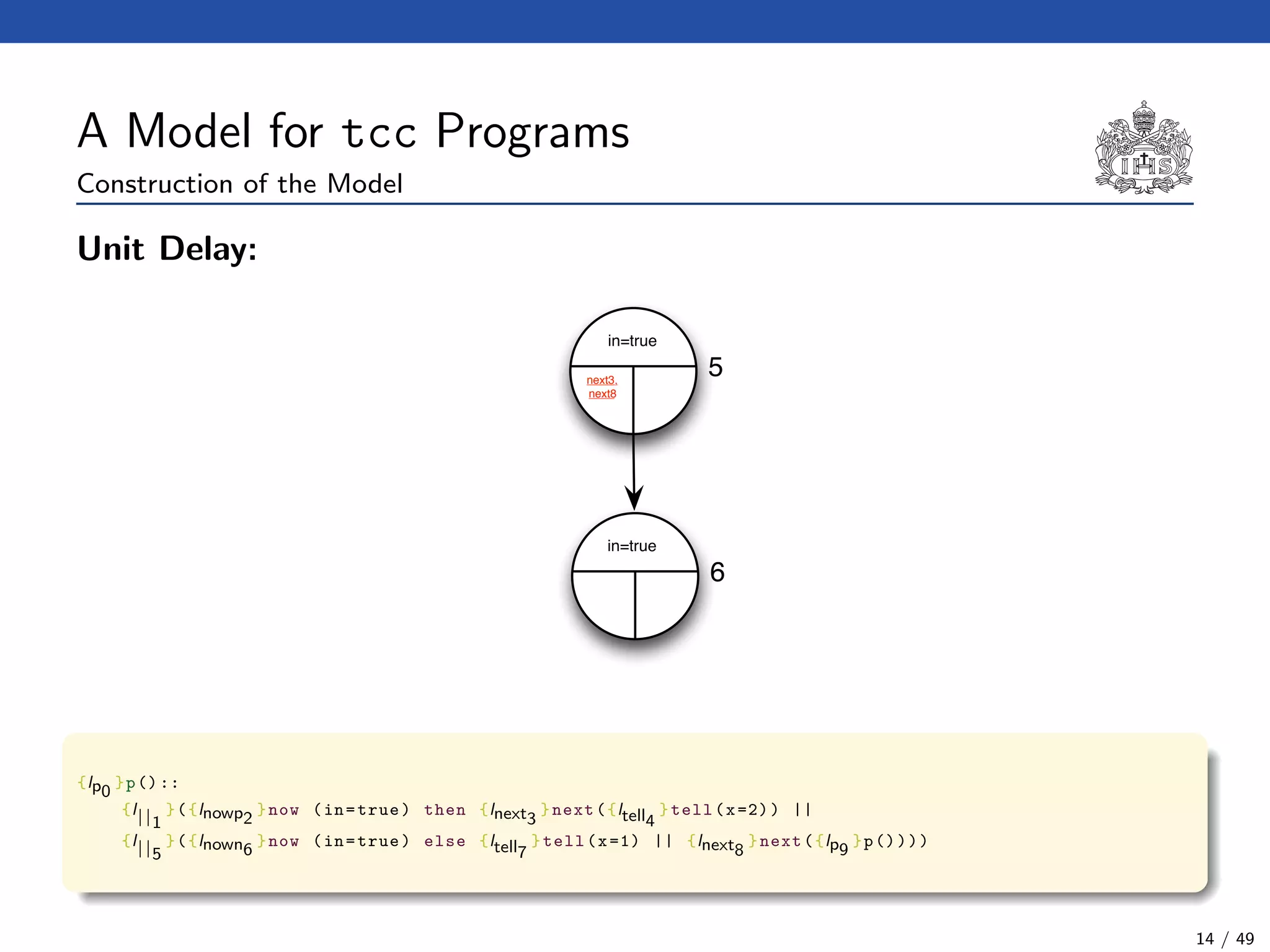
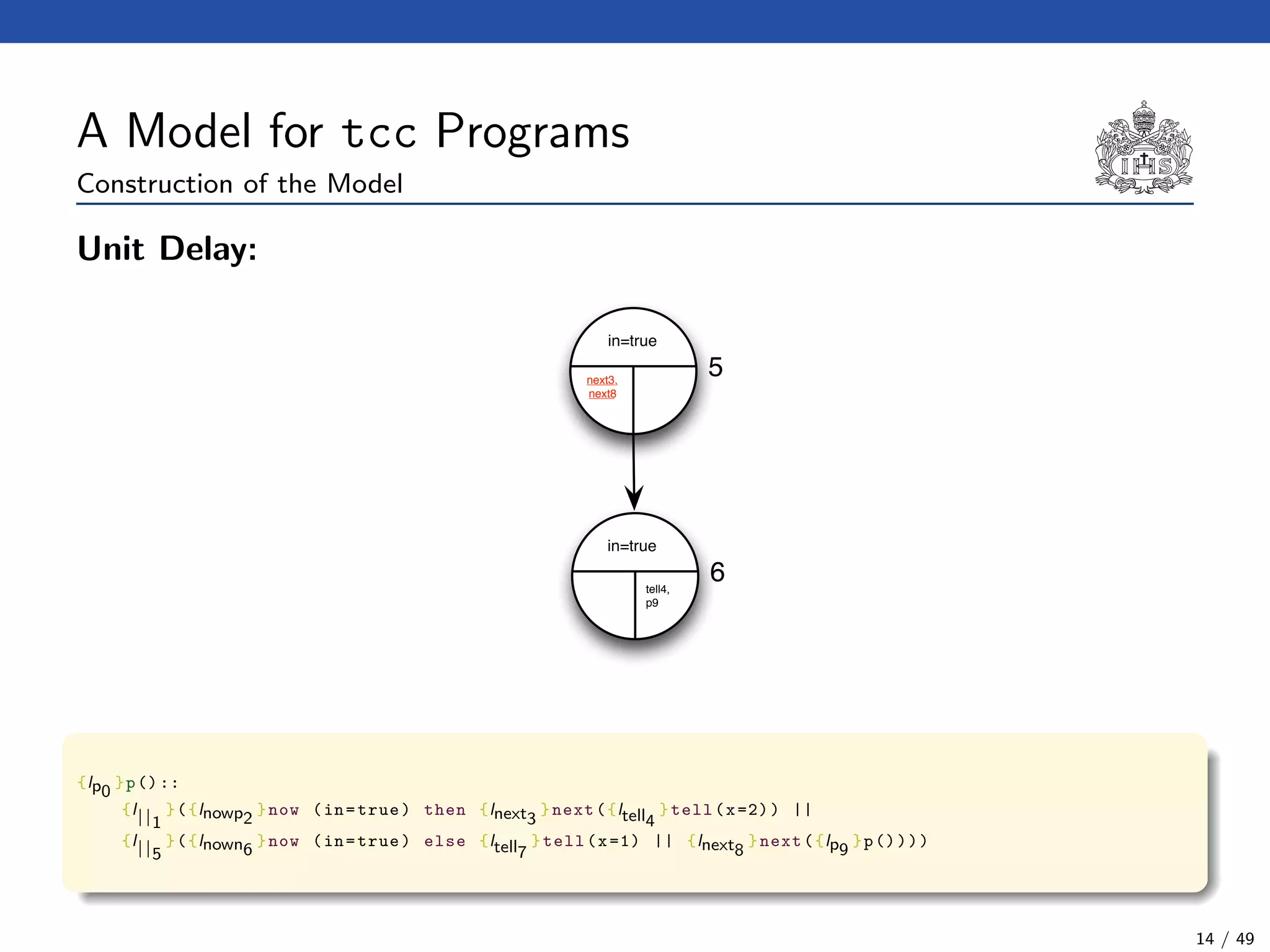
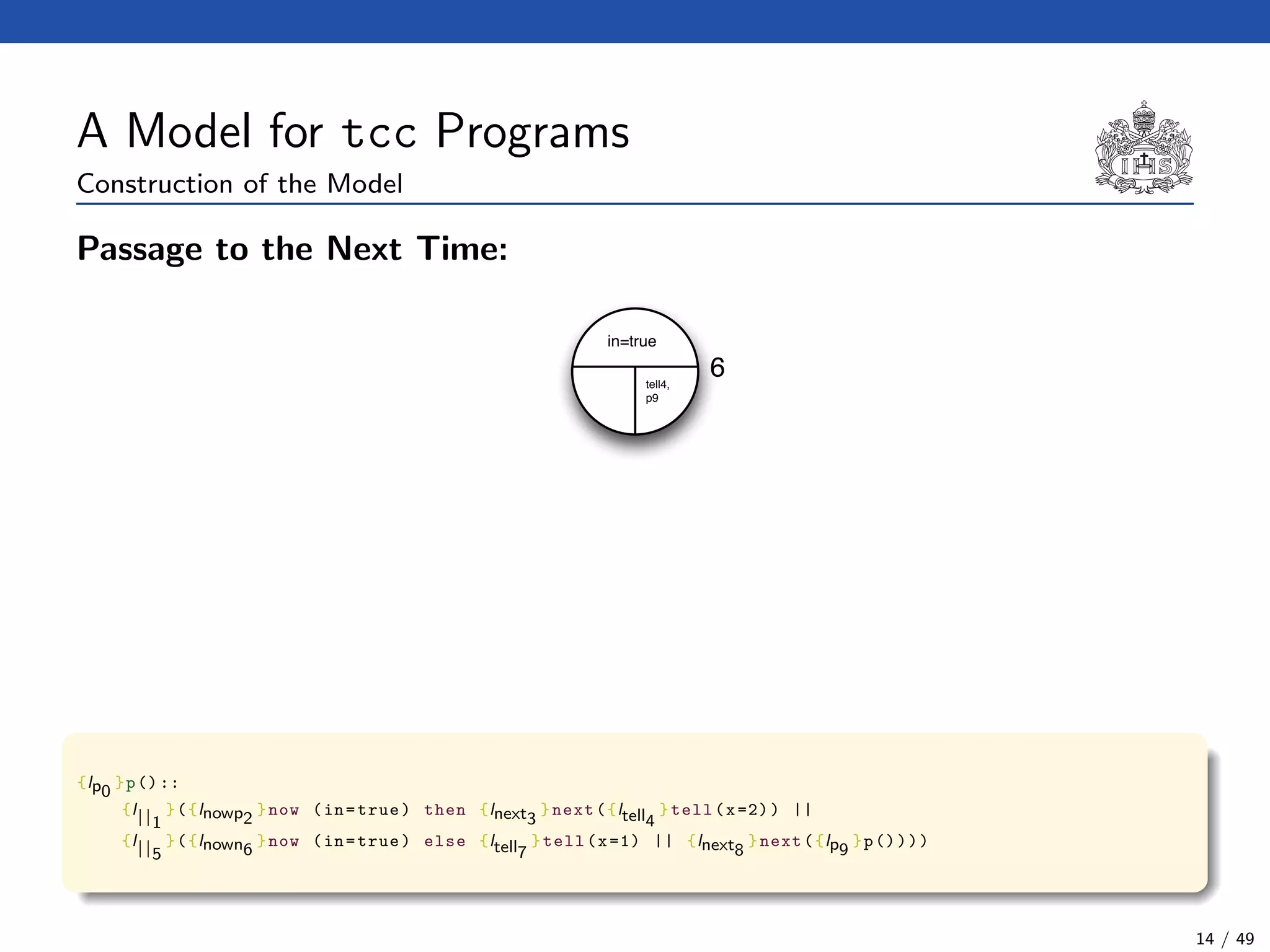
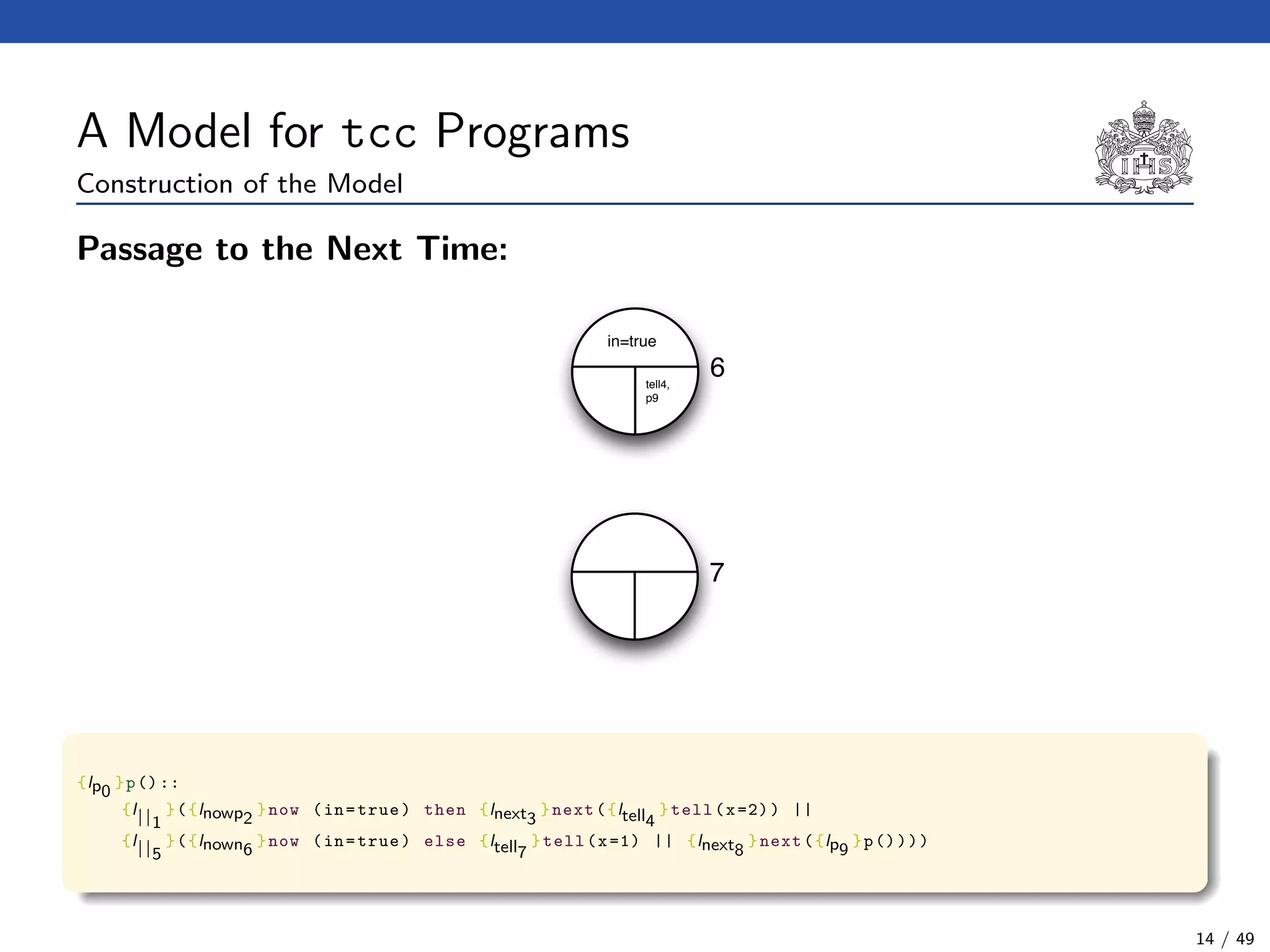
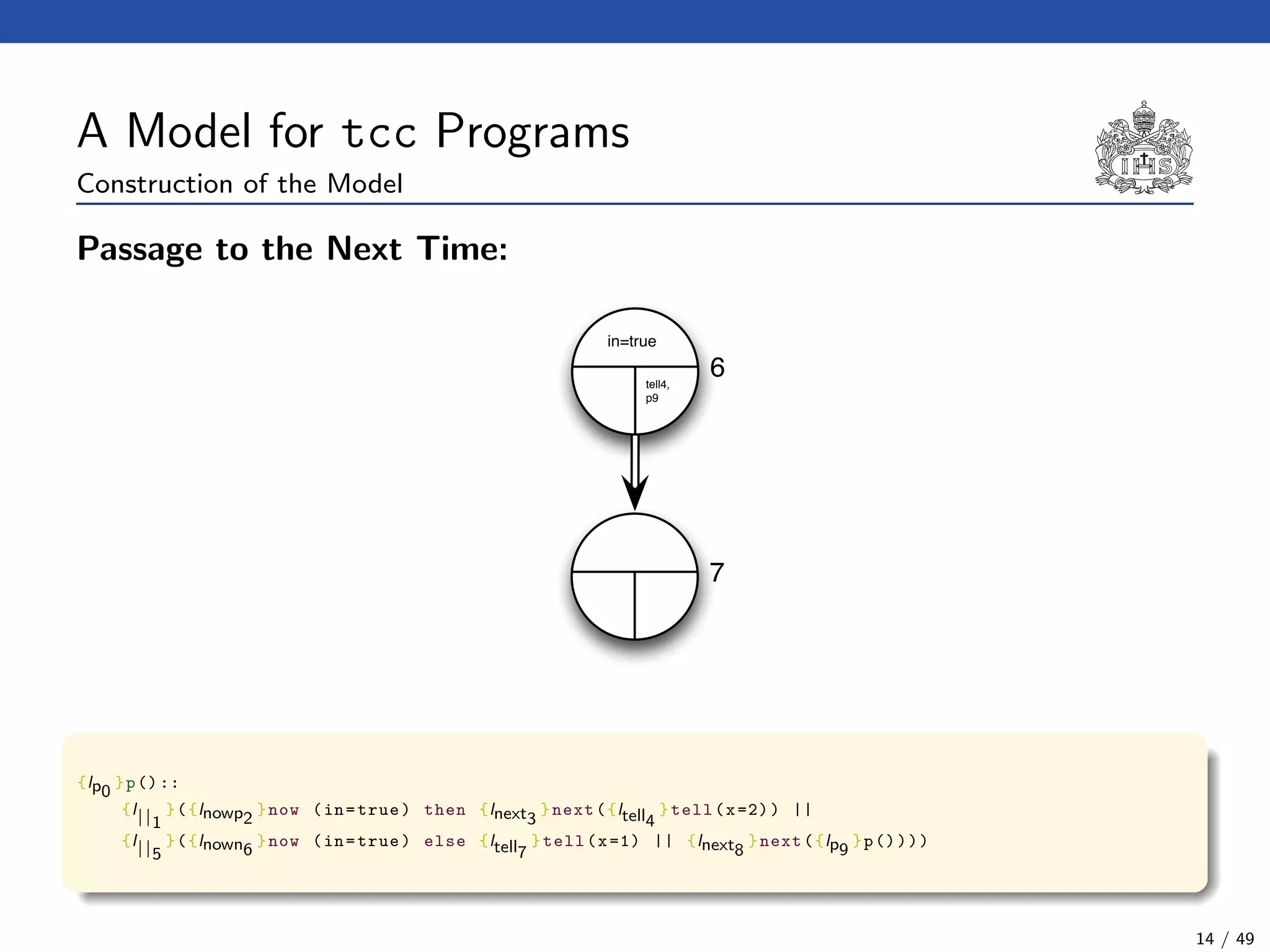
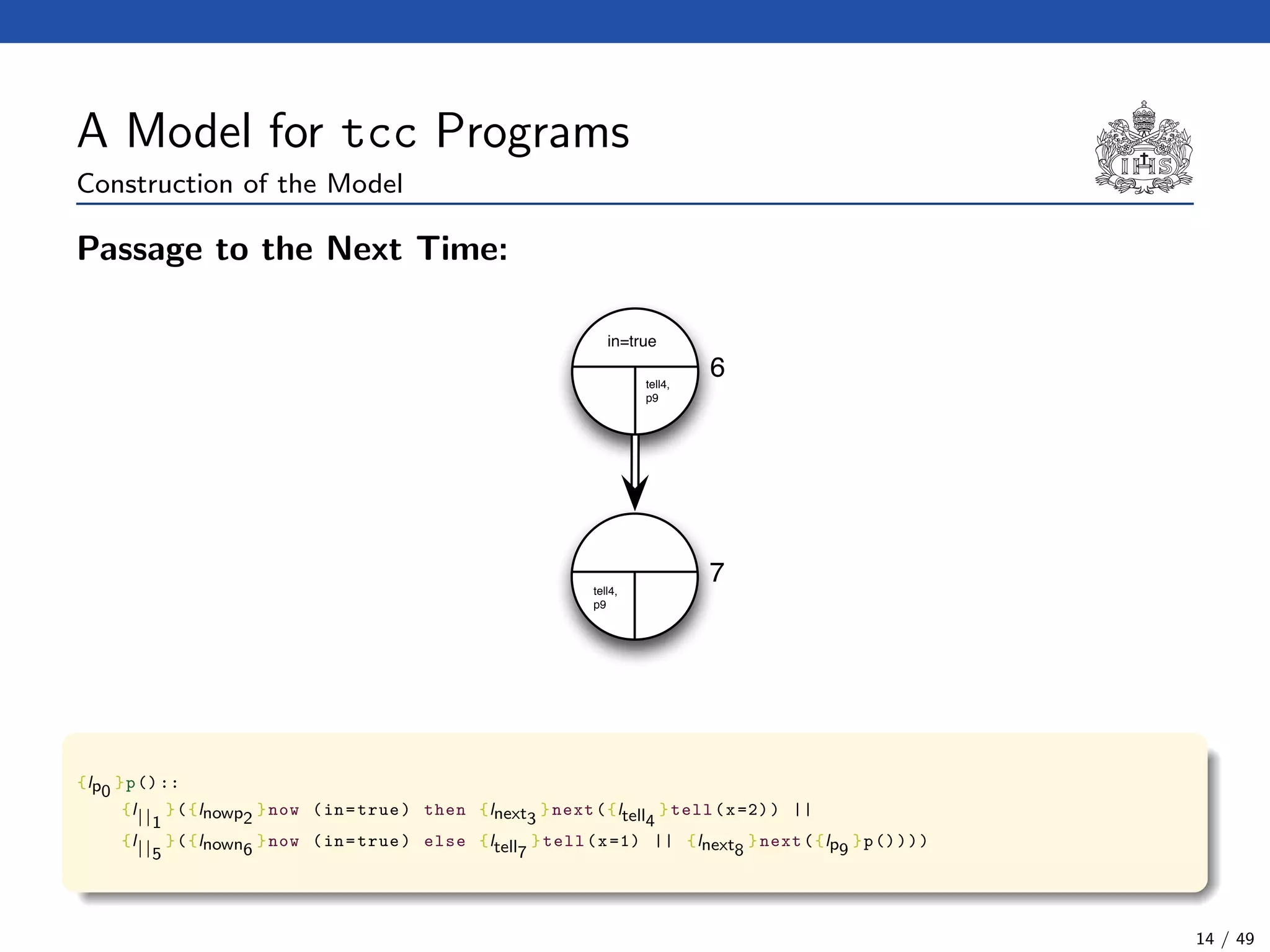
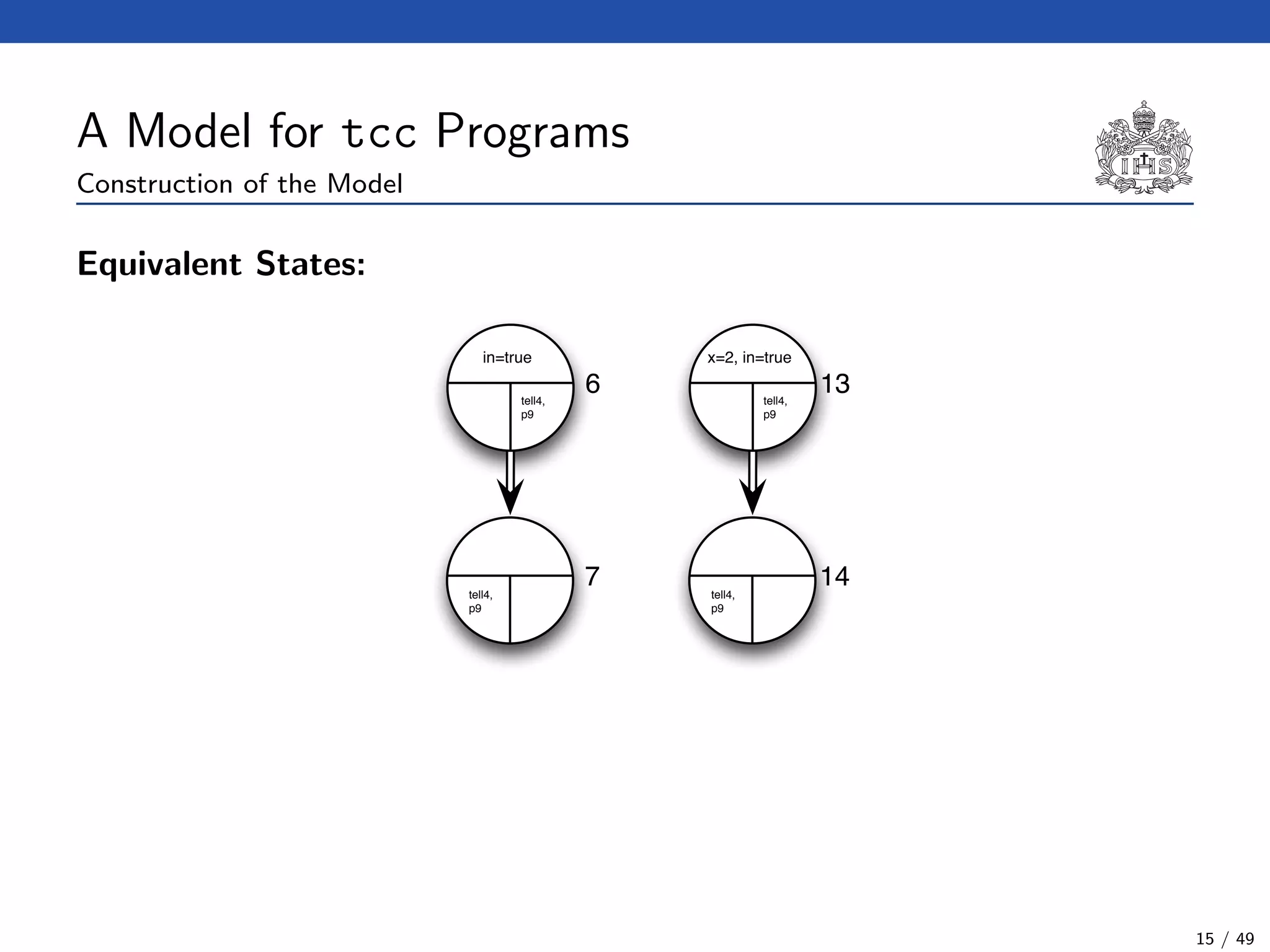
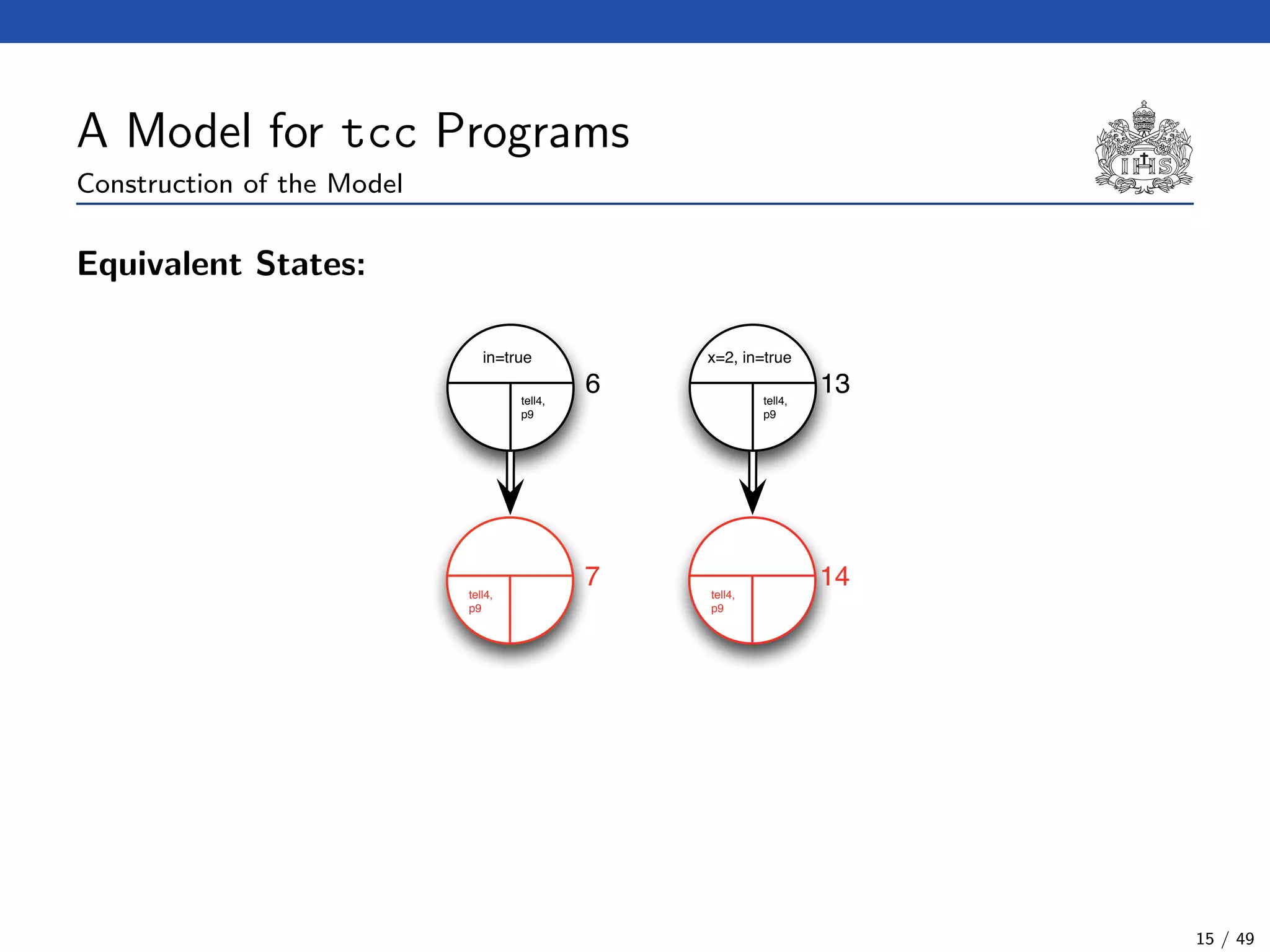
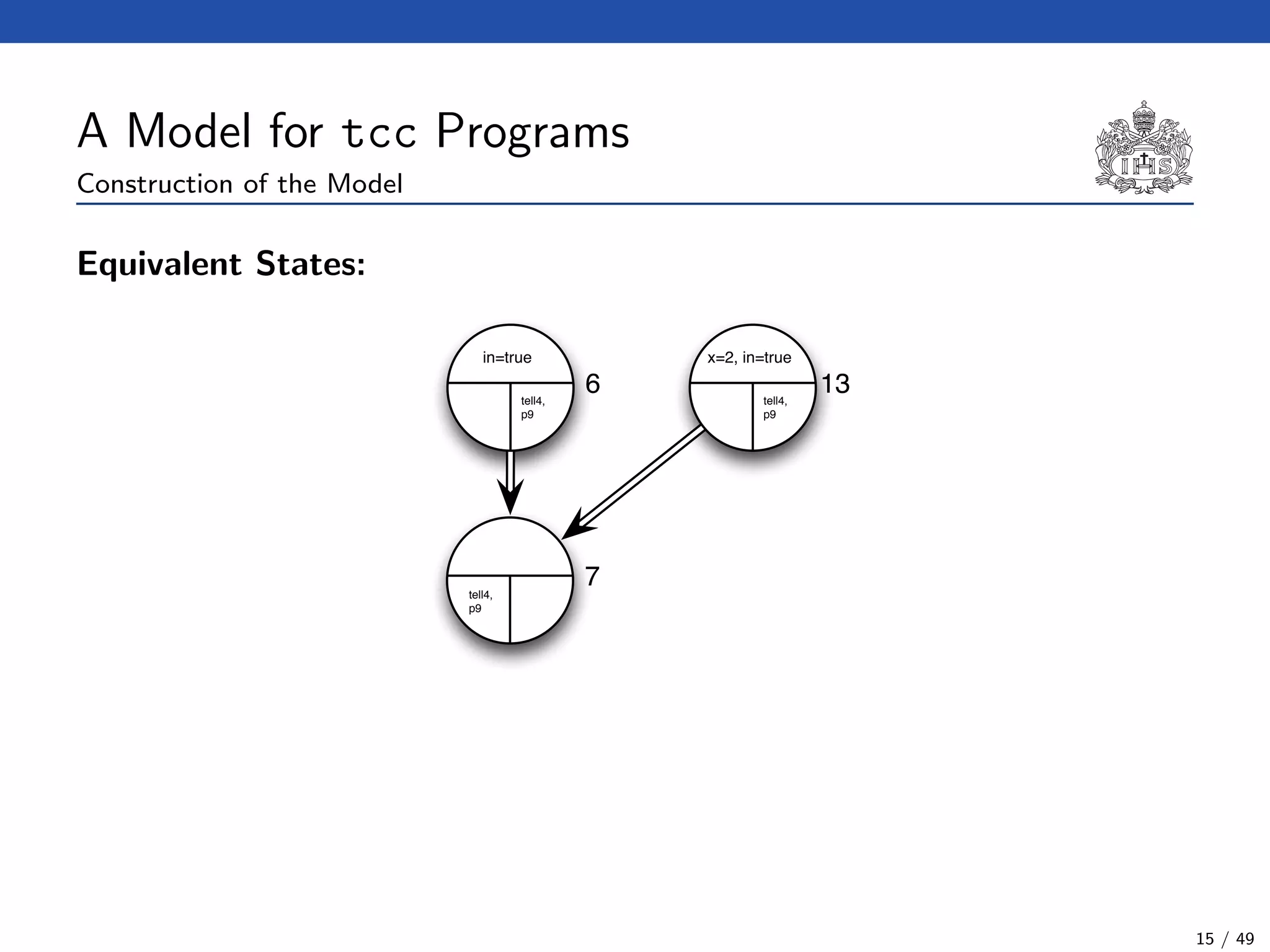
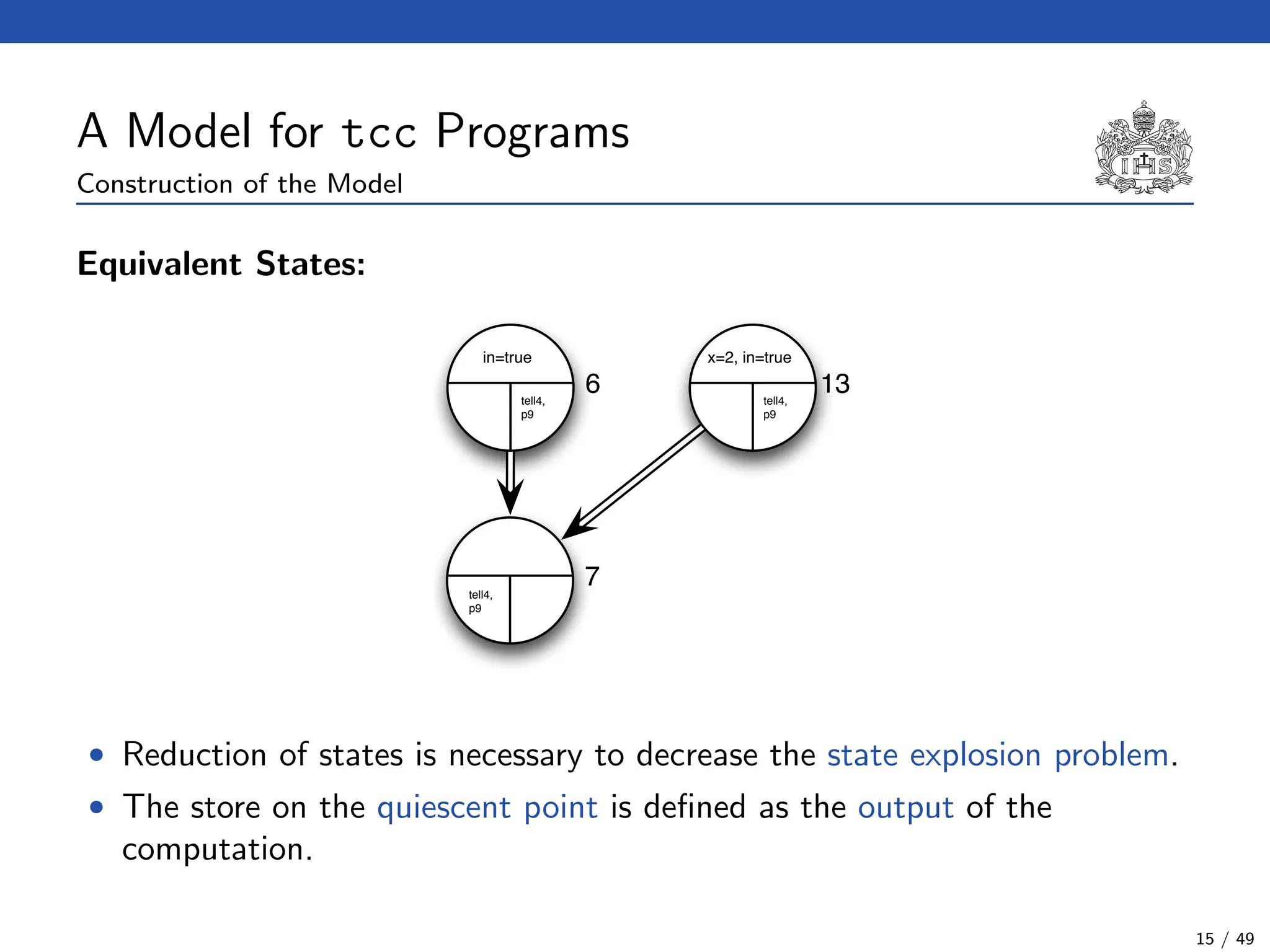
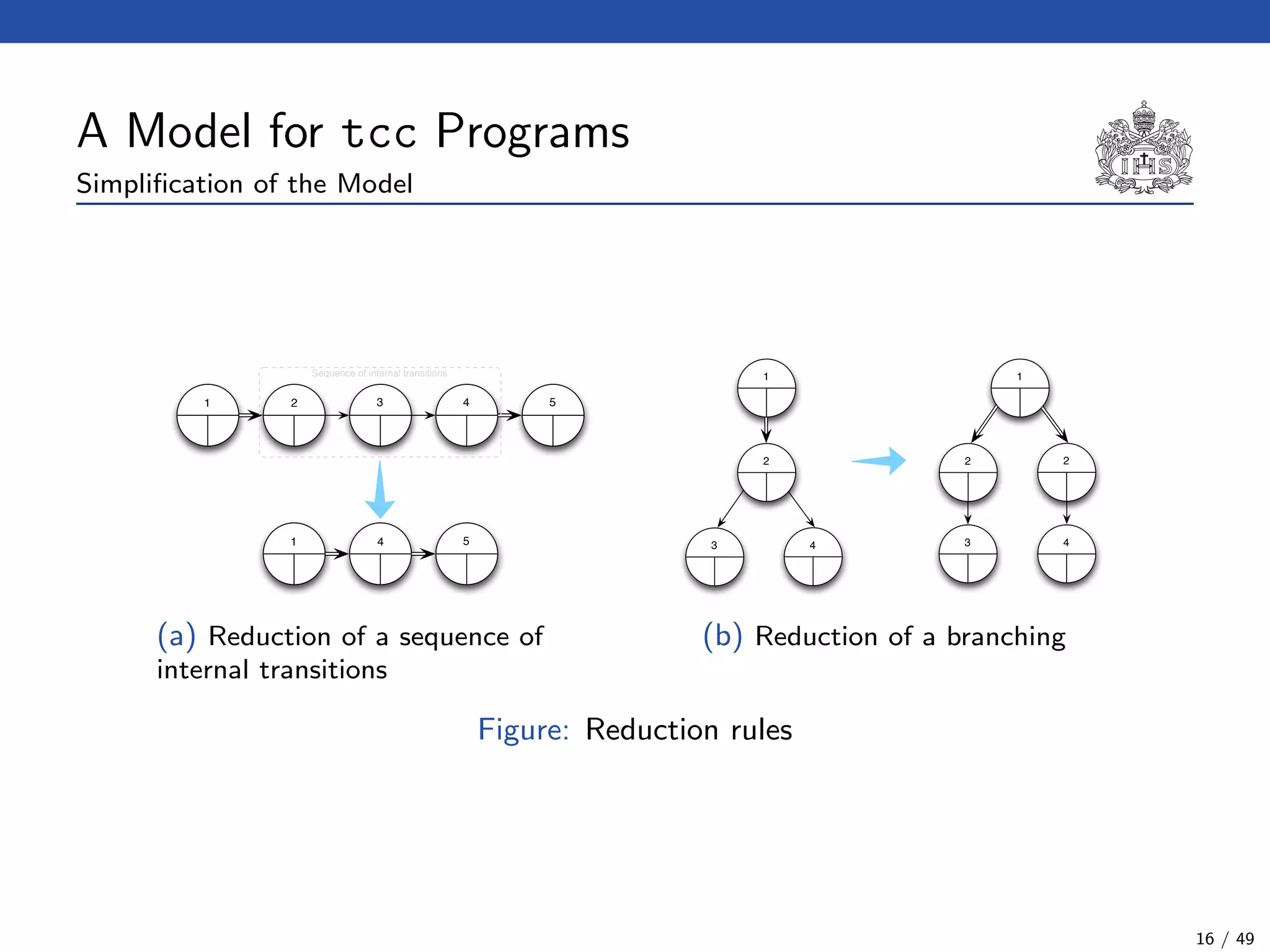
65. The Model Checking Algorithm
• Classical tableau algorithm for the LTL model checking
problem [CGP99, MP95, LP85].
• To prove that a property is satisfied, it is possible to prove that there is no
path in the model checking graph satisfying the negation of the formula.
20 / 49

66. The Model Checking Algorithm
Algorithm:
1. To construct the model checking graph using the negation of φ (i.e. ¬φ).
Definition
21 / 49

67. The Model Checking Algorithm
Algorithm:
1. To construct the model checking graph using the negation of φ (i.e. ¬φ).
Definition
◦ First of all, we have to compute the closure CL(¬φ). This closure is
reminiscent to the Fisher Ladner’s one [MP95, FL79]. Definition
21 / 49

68. The Model Checking Algorithm
Algorithm:
1. To construct the model checking graph using the negation of φ (i.e. ¬φ).
Definition
◦ First of all, we have to compute the closure CL(¬φ). This closure is
reminiscent to the Fisher Ladner’s one [MP95, FL79]. Definition
2. To look for a sequence such that starting from an initial node of the
graph that satisfies the negation of φ, it reaches a self-fulfilling strongly
connected component.
21 / 49

69. The Model Checking Algorithm
Algorithm:
1. To construct the model checking graph using the negation of φ (i.e. ¬φ).
Definition
◦ First of all, we have to compute the closure CL(¬φ). This closure is
reminiscent to the Fisher Ladner’s one [MP95, FL79]. Definition
2. To look for a sequence such that starting from an initial node of the
graph that satisfies the negation of φ, it reaches a self-fulfilling strongly
connected component.
3. If we find a self-fulfilling SCC in the graph, then the system satisfies the
property represented by the negated formula (i.e. the model does not
satisfy the property).
21 / 49

70. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
22 / 49

71. Advantages and drawbacks of Arias’ prototype
• Advantages
◦ Does not require the number of time units as input
◦ The size of the closure of the formula is reasonable small
◦ State explosion is reduced due to tableau method
◦ Does not require a sequence of n inputs
◦ Does not require to compute automata complementation nor
determinization
23 / 49

72. Advantages and drawbacks of Arias’ prototype
• Advantages
◦ Does not require the number of time units as input
◦ The size of the closure of the formula is reasonable small
◦ State explosion is reduced due to tableau method
◦ Does not require a sequence of n inputs
◦ Does not require to compute automata complementation nor
determinization
• Drawbacks
◦ It is not efficient
◦ It is imperative
◦ Does not build automatically the tcc structure
◦ Does not use constraint deduction
◦ Does not output the counter-example
◦ Does not support non-deterministic choice
◦ Does not support local processes
23 / 49

73. Advantages and drawbacks of Mozart/OZ’s
implementation
• To adapt the implementation to ntcc, instead of “now,else”, we use
“unless,next” and instead of procedure calls, we use “bang”
24 / 49

74. Advantages and drawbacks of Mozart/OZ’s
implementation
• To adapt the implementation to ntcc, instead of “now,else”, we use
“unless,next” and instead of procedure calls, we use “bang”
• Advantages
◦ Does not require the number of time units as input
◦ The size of the closure of the formula is reasonable small
◦ State explosion is reduced due to tableau method
◦ Does not require the a sequence of n inputs
◦ Does not require to compute automata complementation nor
determinization
◦ Is extended for ntcc syntax
◦ It is mostly declarative (functional)
◦ Builds automatically the ntcc structure
◦ Uses constraint deduction
◦ Exhibits the counter-example
24 / 49

75. Advantages and drawbacks of Mozart/OZ’s
implementation
• To adapt the implementation to ntcc, instead of “now,else”, we use
“unless,next” and instead of procedure calls, we use “bang”
• Advantages
◦ Does not require the number of time units as input
◦ The size of the closure of the formula is reasonable small
◦ State explosion is reduced due to tableau method
◦ Does not require the a sequence of n inputs
◦ Does not require to compute automata complementation nor
determinization
◦ Is extended for ntcc syntax
◦ It is mostly declarative (functional)
◦ Builds automatically the ntcc structure
◦ Uses constraint deduction
◦ Exhibits the counter-example
• Drawbacks
◦ Does not support non-deterministic choice
◦ Does not suppor local processes
24 / 49

76. Outline
1 Introduction
2 Previous work
3 The Model Checking Technique
4 A Model for tcc Programs
5 A Logic for the Specification of Properties
6 The Model Checking Algorithm
7 Implementation
8 Concluding Remarks
25 / 49

77. Summary
• At present, ntcc does not provide for the automatic, or even
machine-assisted, verification of system properties.
26 / 49

78. Summary
• At present, ntcc does not provide for the automatic, or even
machine-assisted, verification of system properties.
• Previous work on verification for ntcc has not been satisfactory
26 / 49

79. Summary
• At present, ntcc does not provide for the automatic, or even
machine-assisted, verification of system properties.
• Previous work on verification for ntcc has not been satisfactory
• The implementation of Arias’ algorithms in Mozart/OZ, ntccKMC
◦ Can be downloaded from http://ntcckmc.sourceforge.net
◦ Is extended for ntcc syntax
◦ Builds automatically the ntcc structure
◦ Uses constraint deduction
◦ Exhibits the counter-example
◦ Does not support non-deterministic choice (easy to solve)
◦ Does not support local processes (hard to solve)
26 / 49

80. Thank you!

81. References (1)
Edmund M. Clarke, Orna Grumberg, and Doron A. Peled.
Model Checking.
MIT Press, Cambridge, 1999.
Michael J. Fischer and Richard E. Ladner.
Propositional Dynamic Logic of Regular Programs.
Journal of Computer and System Sciences, 18(2):194–211, 1979.
Moreno Falaschi and Alicia Villanueva.
Automatic verification of timed concurrent constraint programs.
Theory and Practice of Logic Program, 6(4):265–300, 2006.
28 / 49

82. References (2)
Hubert Garavel.
Reflections on the Future of Concurrency Theory in General and
Process Calculi in Particular.
In Proceedings of LIX Colloquium on Emergent Trends in Concurrency
Theory, volume 209 of Electronic Notes in Theoretical Computer
Science, pages 149–164. Elsevier, 2008.
Orna Lichtenstein and Amir Pnueli.
Checking that Finite State Concurrent Programs Satisfy their Linear
Specification.
In Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on
Principles of Programming Languages, pages 97–107, New York, NY,
USA, 1985. ACM Press.
Zohar Manna and Amir Pnueli.
Temporal Verification of Reactive Systems: Safety.
Springer-Verlag New York, Inc., 1995.
29 / 49

83. References (3)
Vijay A. Saraswat, Radha Jagadeesan, and Vineet Gupta.
Programming in Timed Concurrent Constraint Languages.
In Constraint Programming: Proceedings 1993, NATO Advanced
Science Institute Series, pages 361–410, Berlin, 1994. Springer-Verlag.
Mauricio Toro-Berm´udez.
Towards a correct and efficient implementation of simulation and
verification tools for probabilistic ntcc.
Technical report, Pontificia Universidad Javeriana, May 2009.
Mauricio Toro-Berm´udez.
Structured Musical Interactive Scores (short).
PhD thesis, Universit´e de Bordeaux, 2012.
Frank D. Valencia.
Decidability of infinite-state timed ccp processes and first-order ltl.
Theor. Comput. Sci., 330(3):557–607, 2005.
30 / 49

84. The Model Checking Algorithm
Definition (Strongly Connected Component)
Given a graph G, we define a Strongly Connected Component (SCC) S as a
maximal subgraph of G such that for every two distinct nodes A, B ∈ S,
there exists a path from A to B that passes through nodes of S.
We say that S is transient if it consists of a single node that is not
connected to itself.
Definition (Self-fulfilling SCC)
Given a model-checking graph G, a self-fulfilling strongly connected
component C is defined as a non-transient strongly connected component in
G which satisfies that for every node n in C and for every ♦φ ∈ Qn there
exists a node m in C such that φ ∈ Qm.
31 / 49

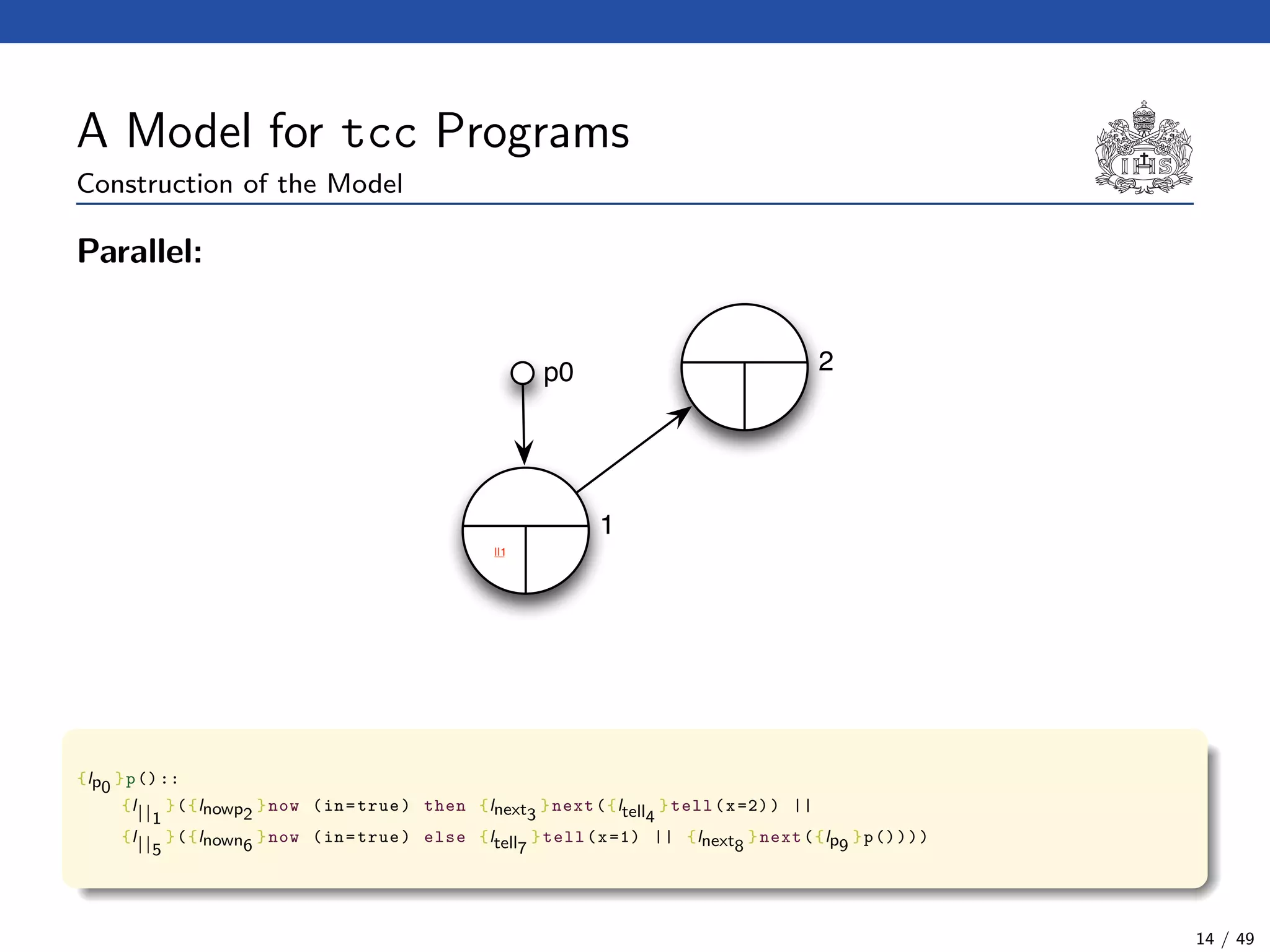
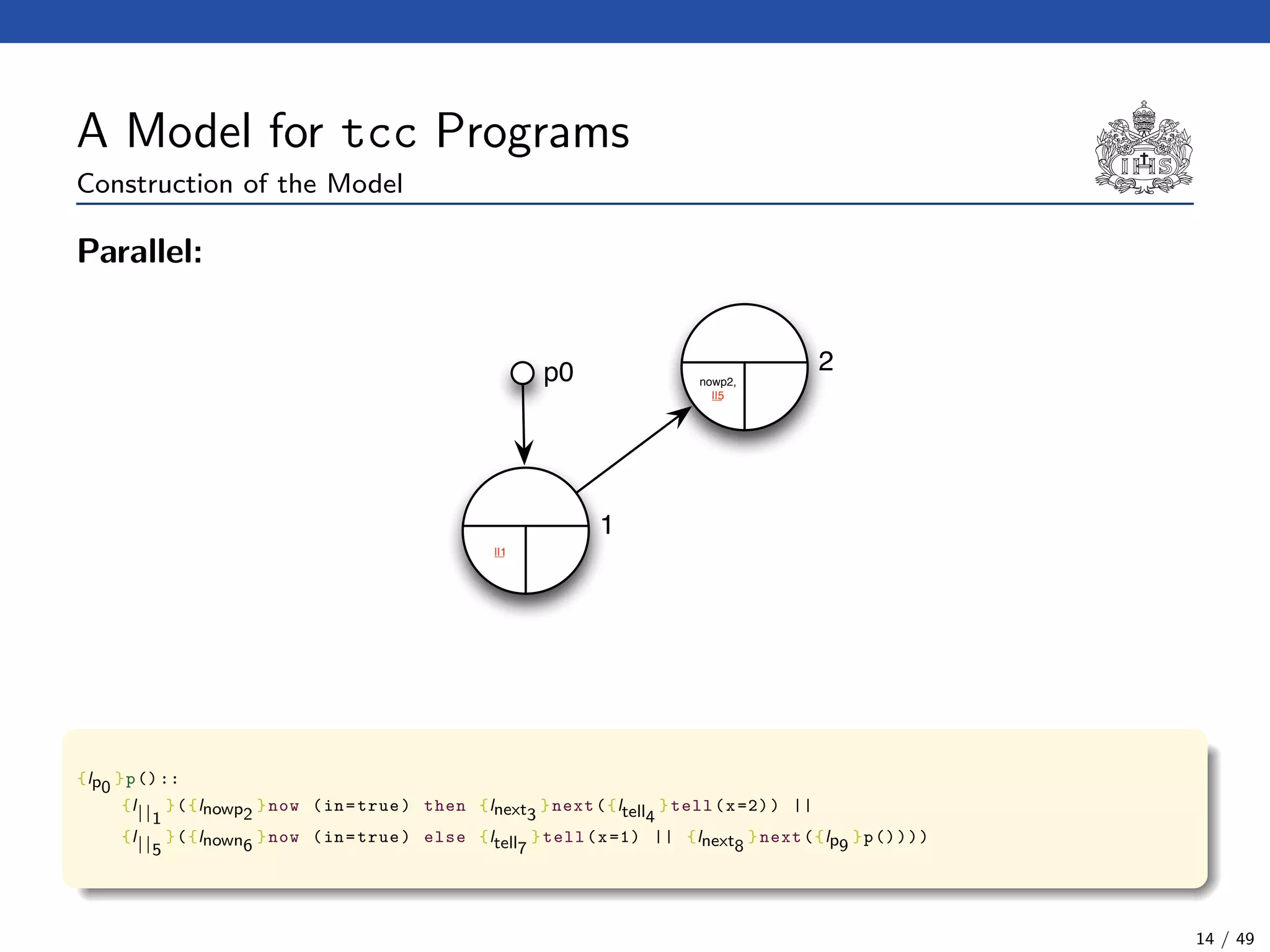
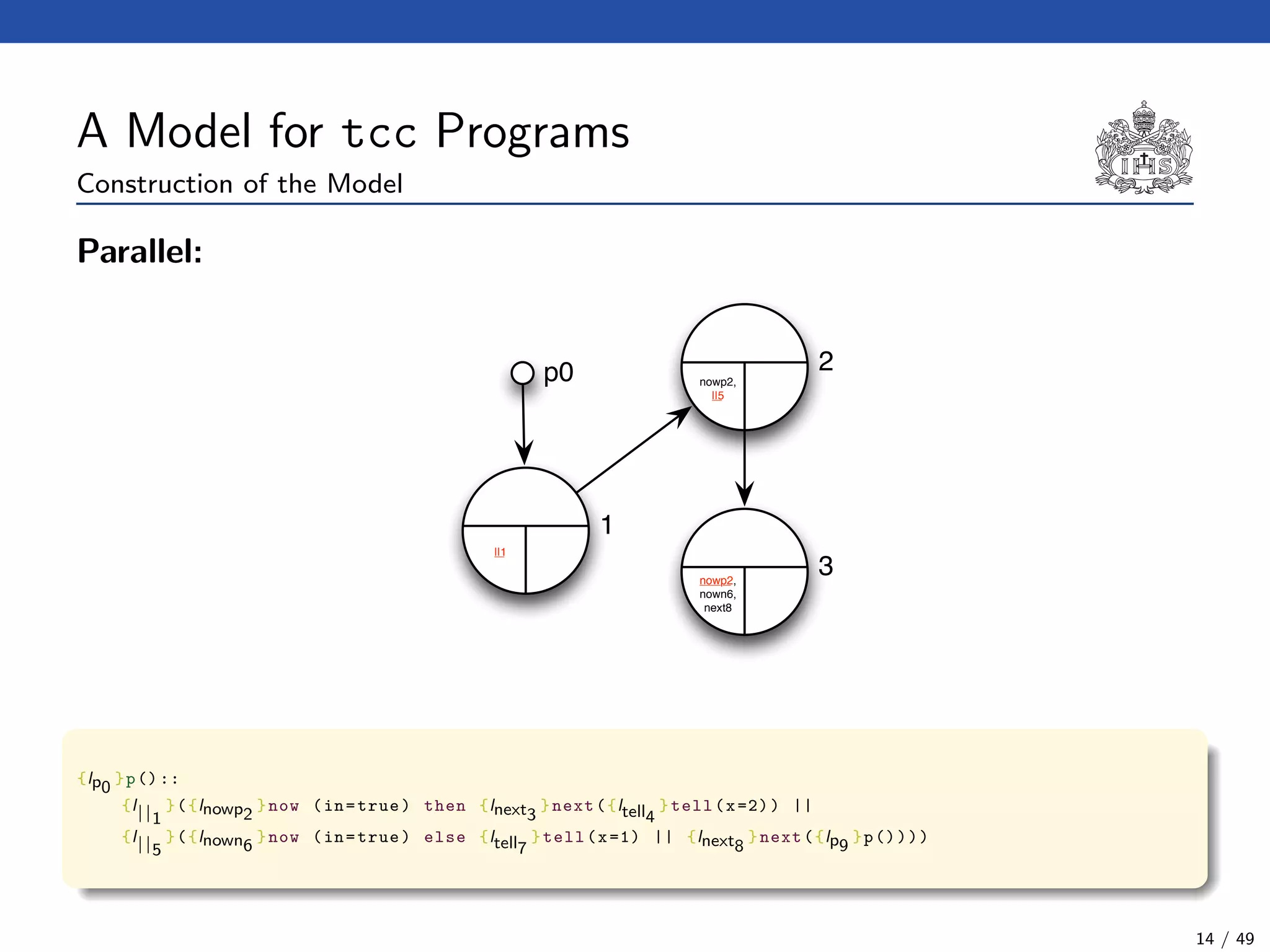
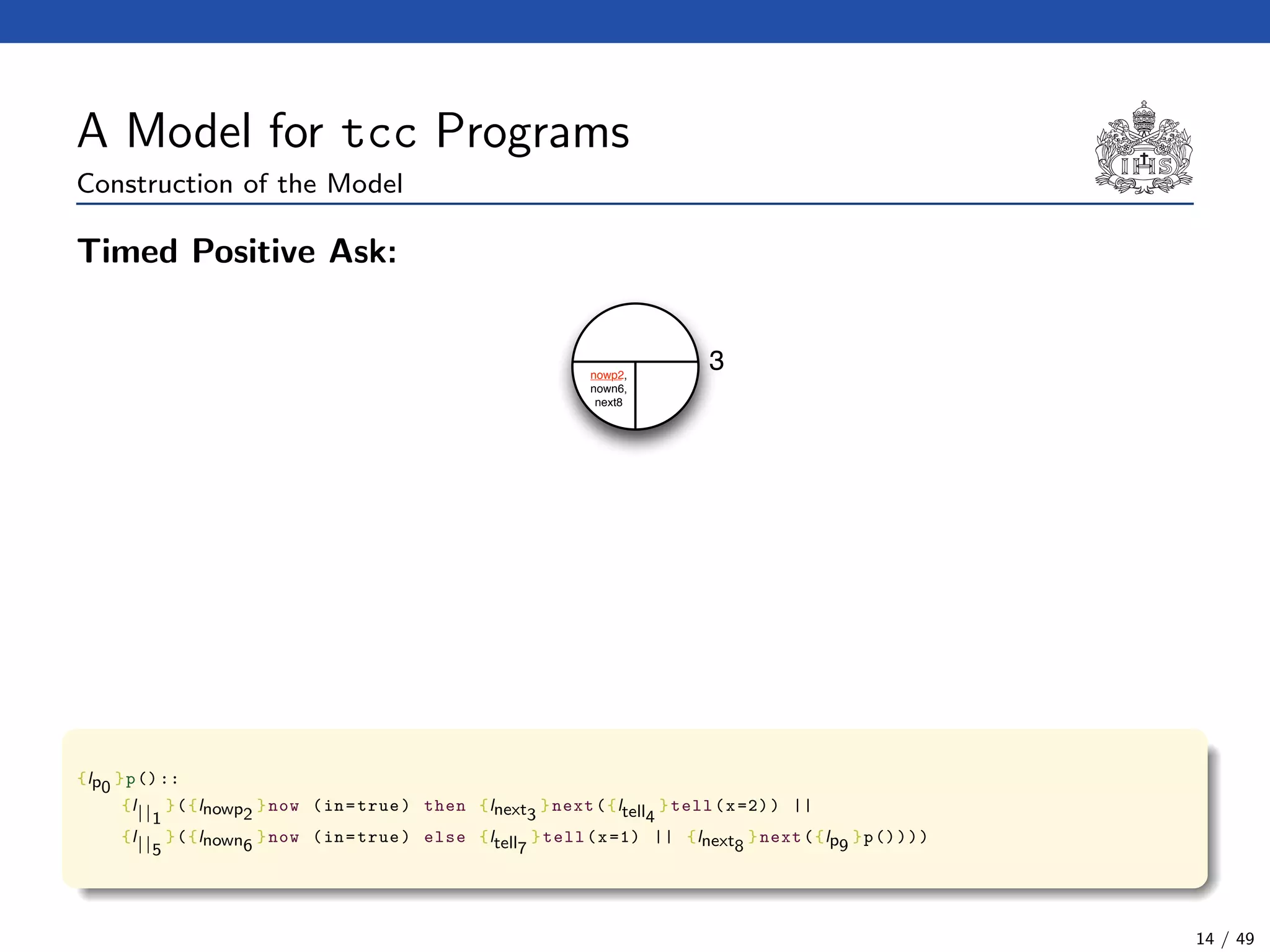
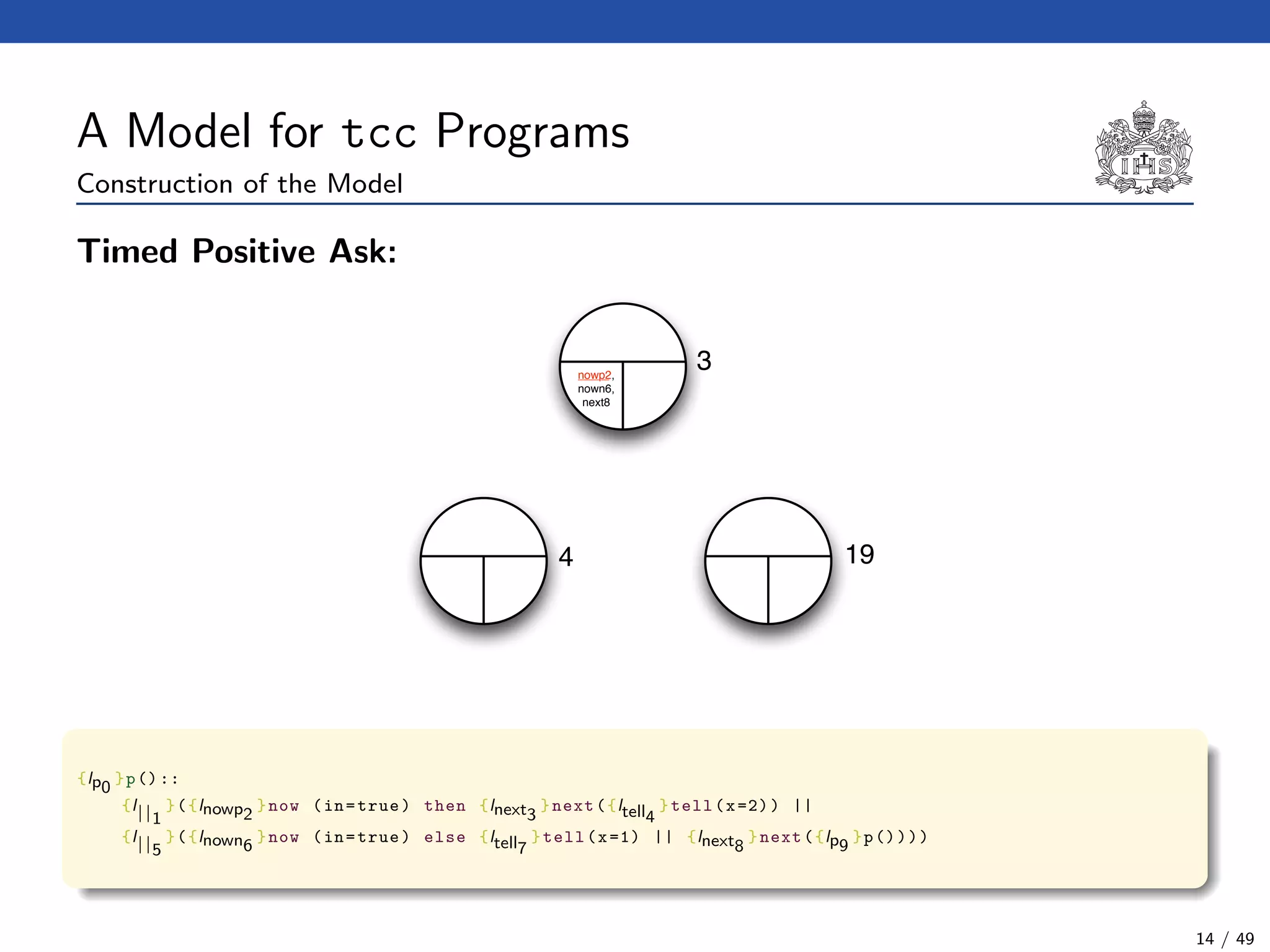
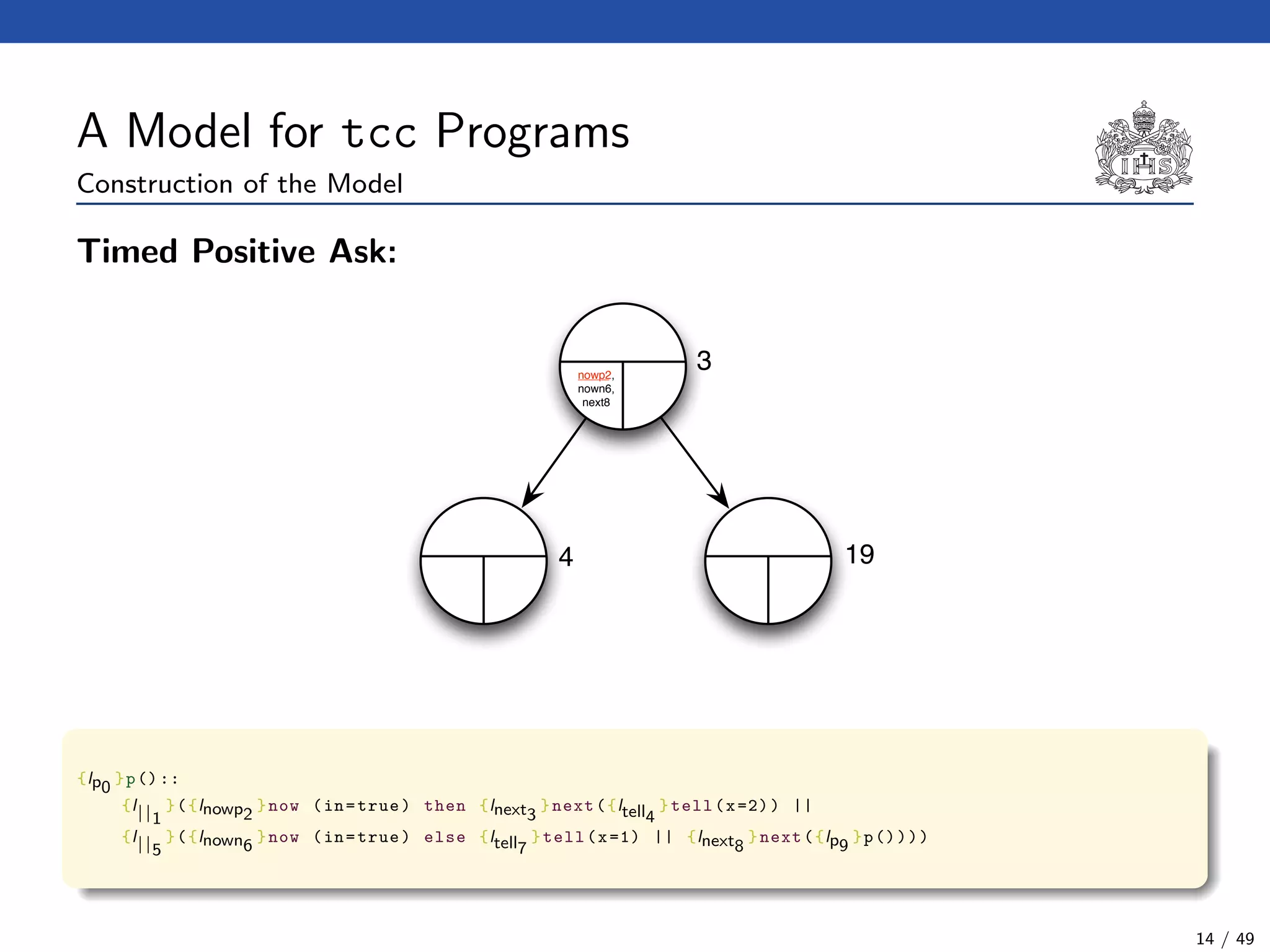
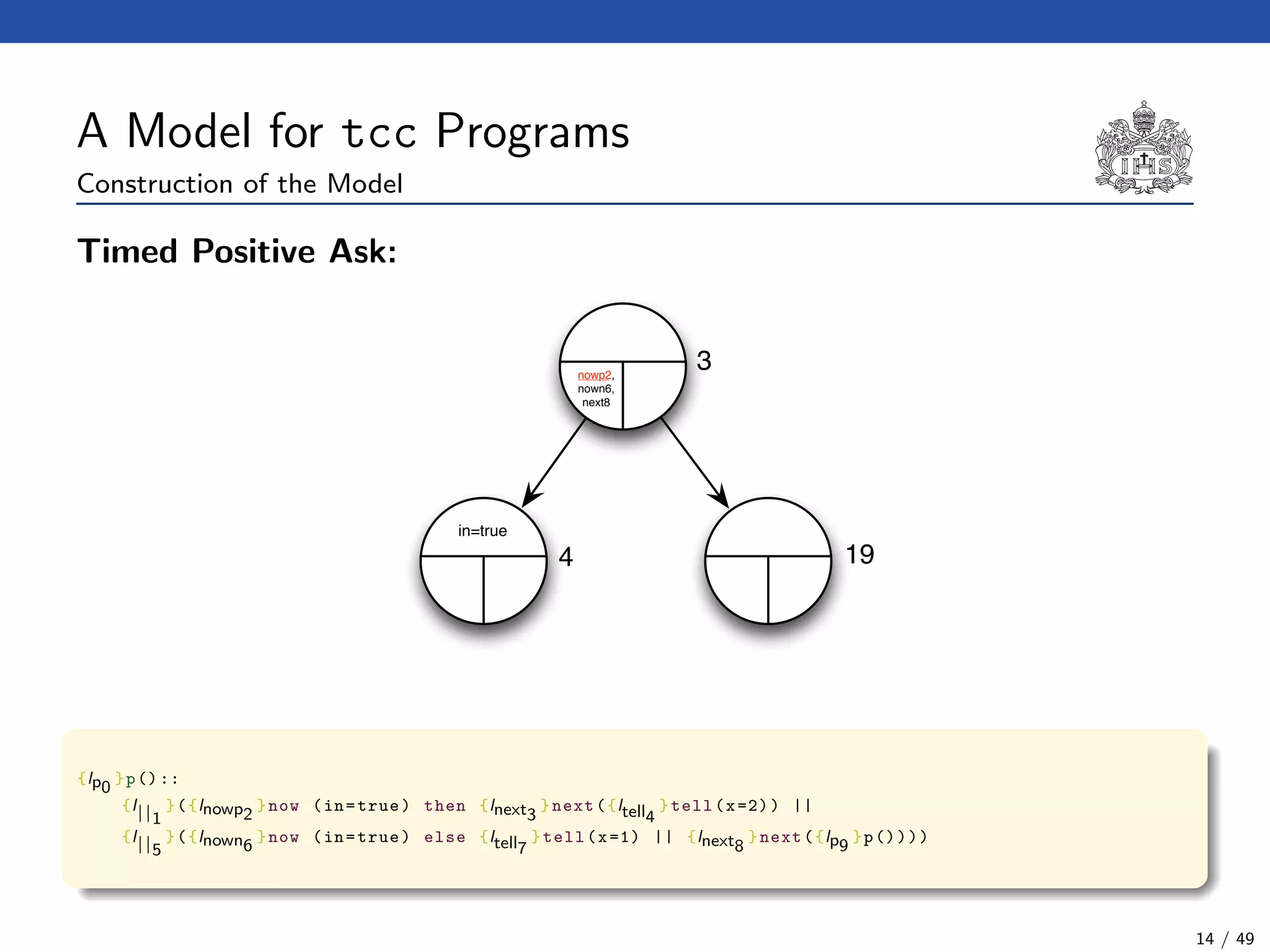
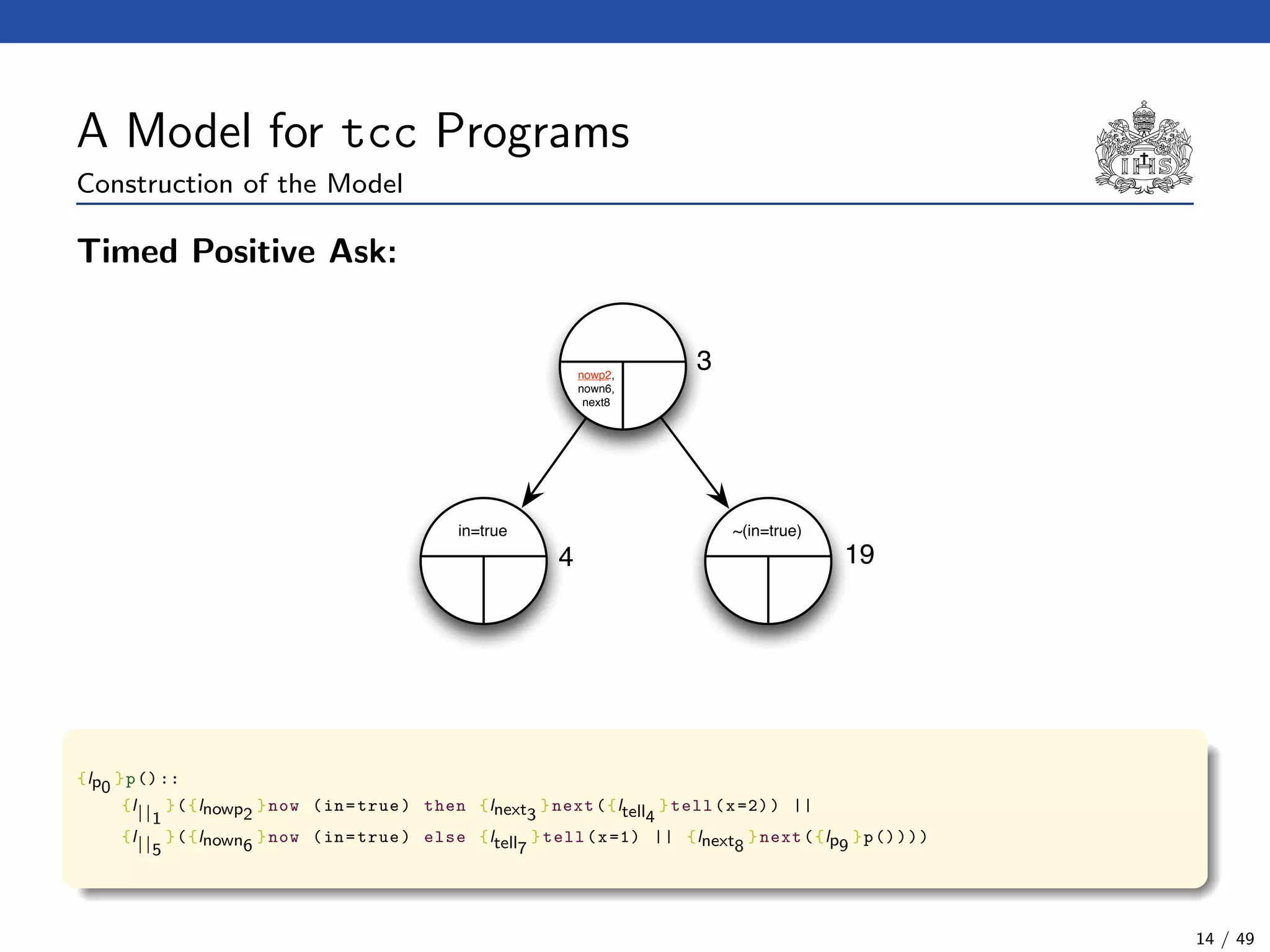
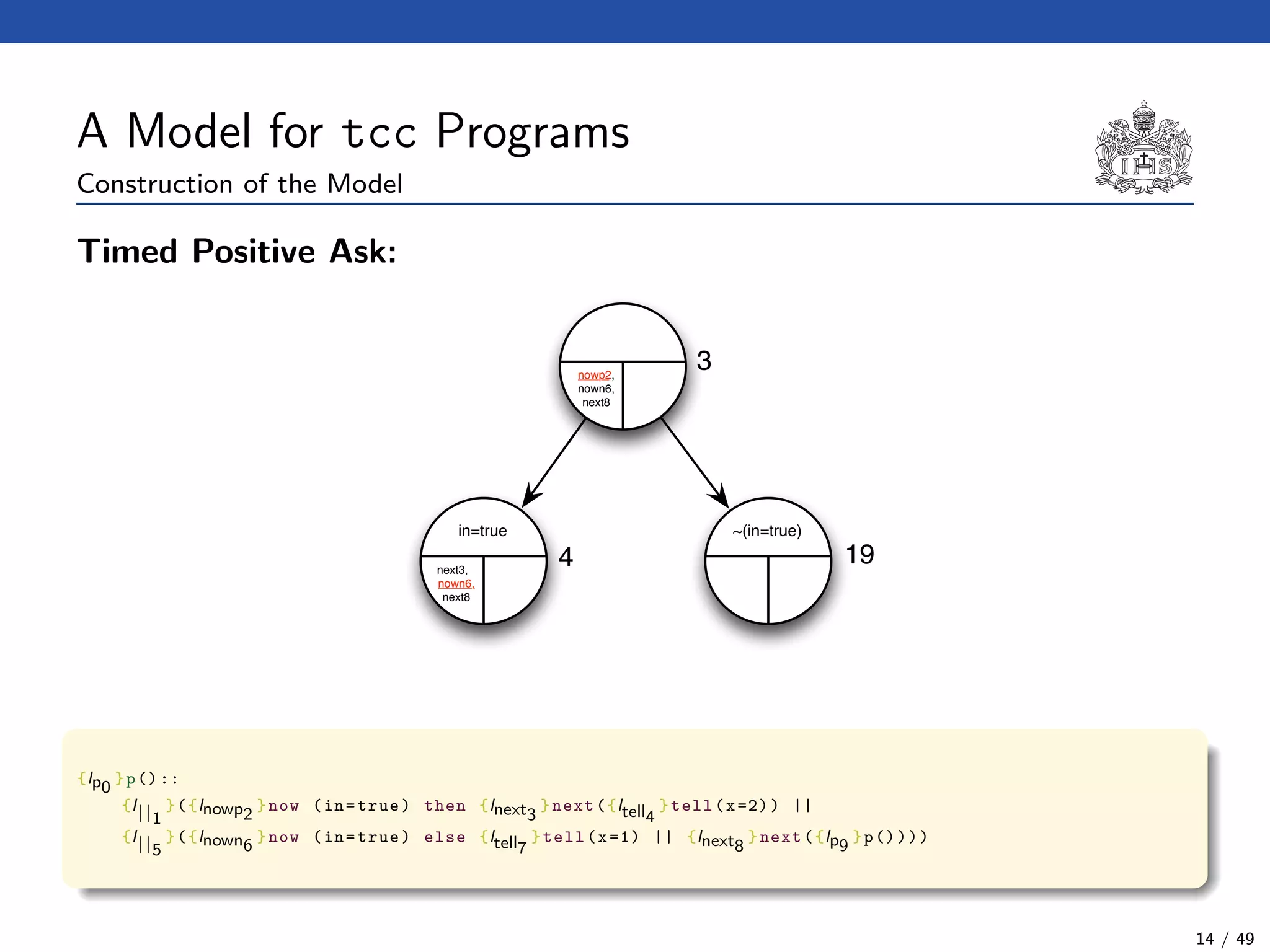
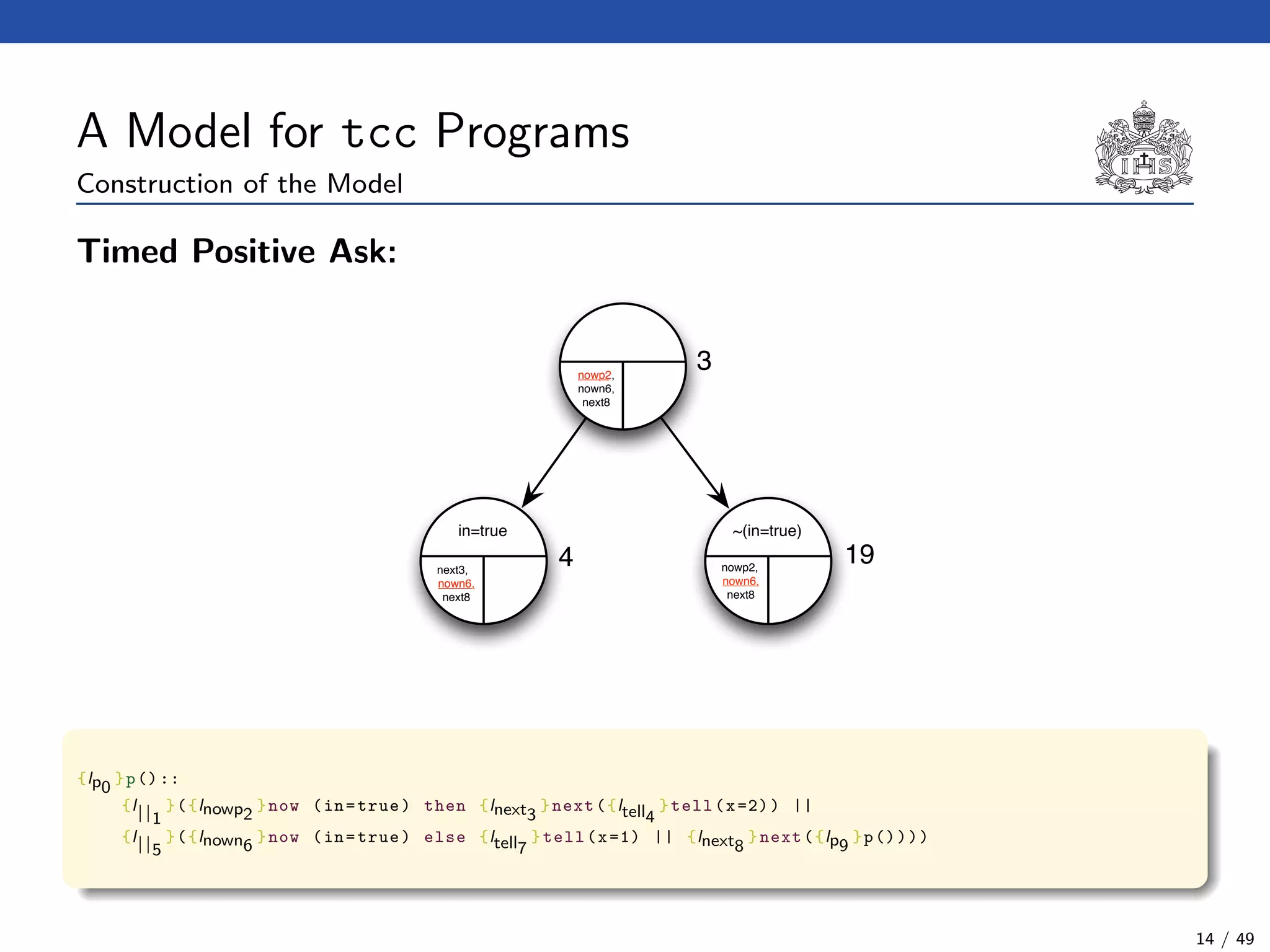
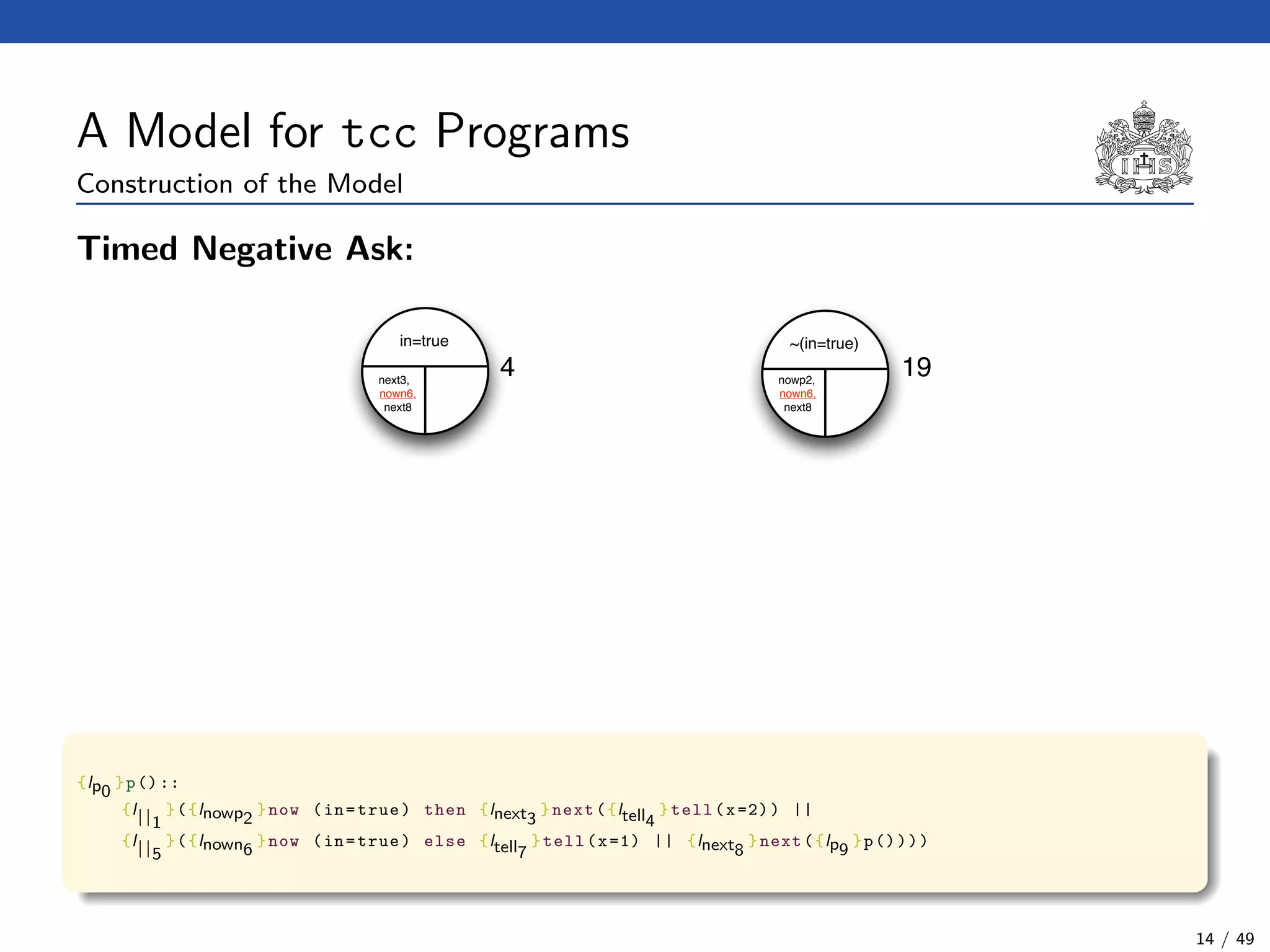
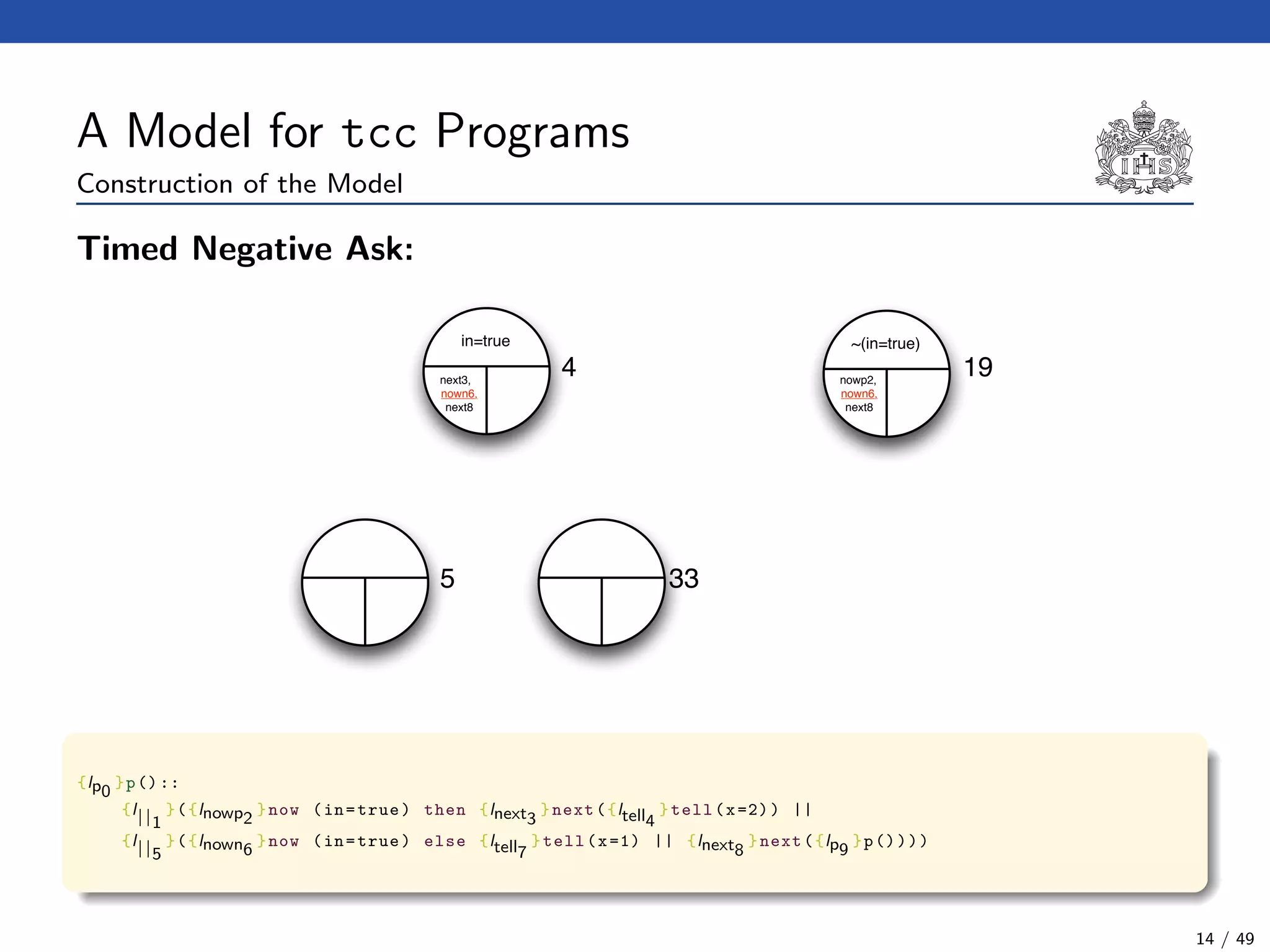
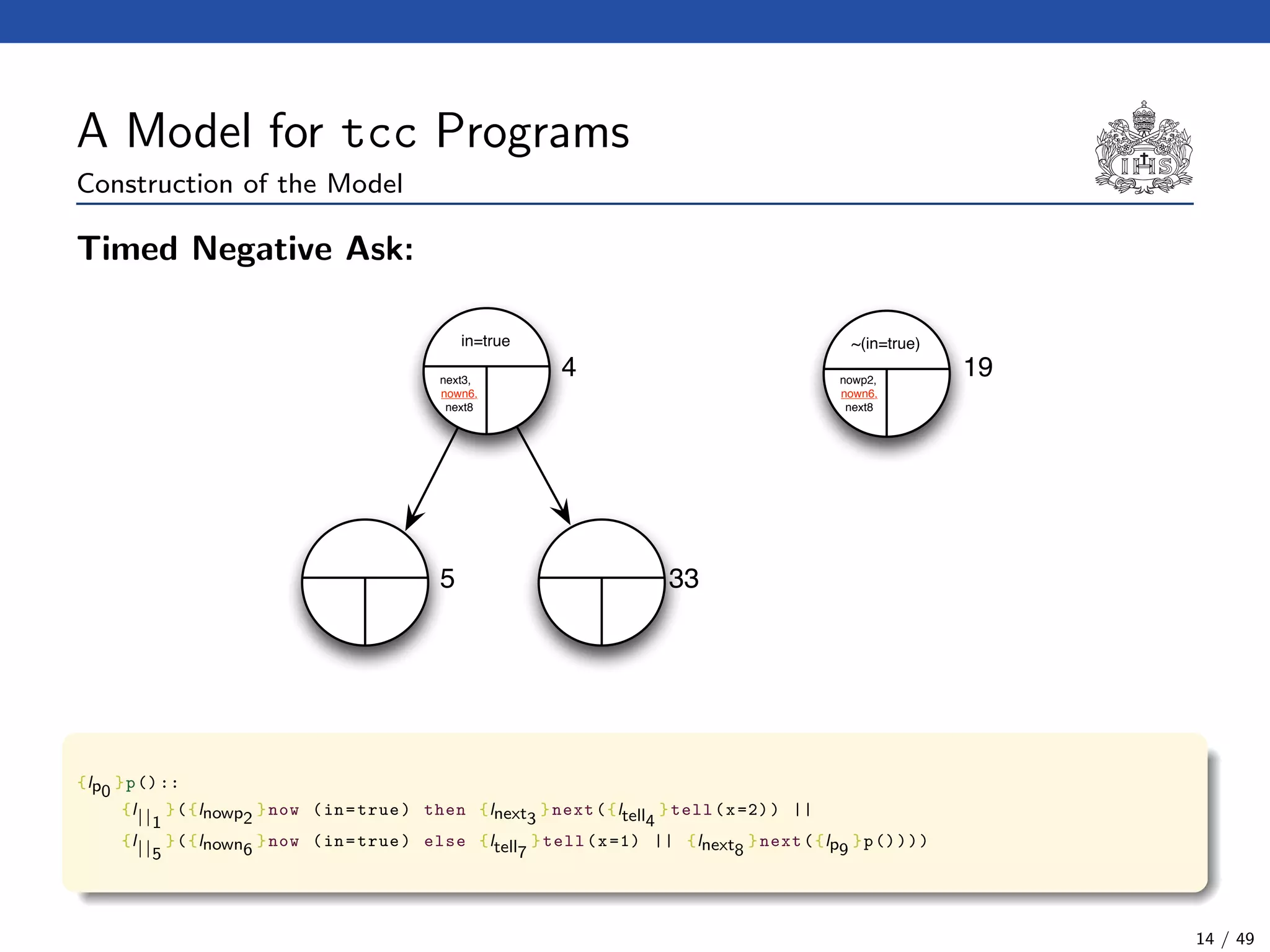
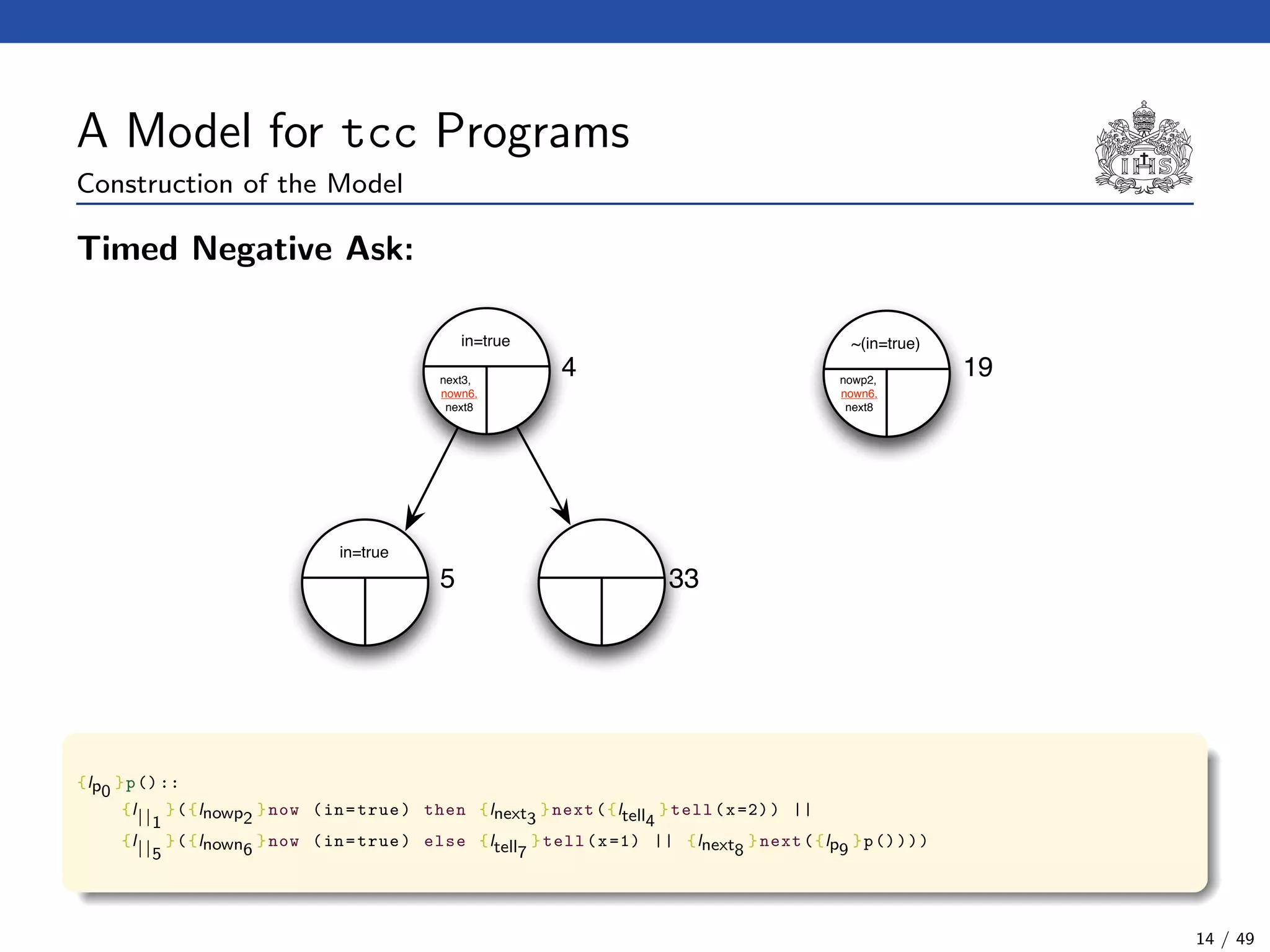
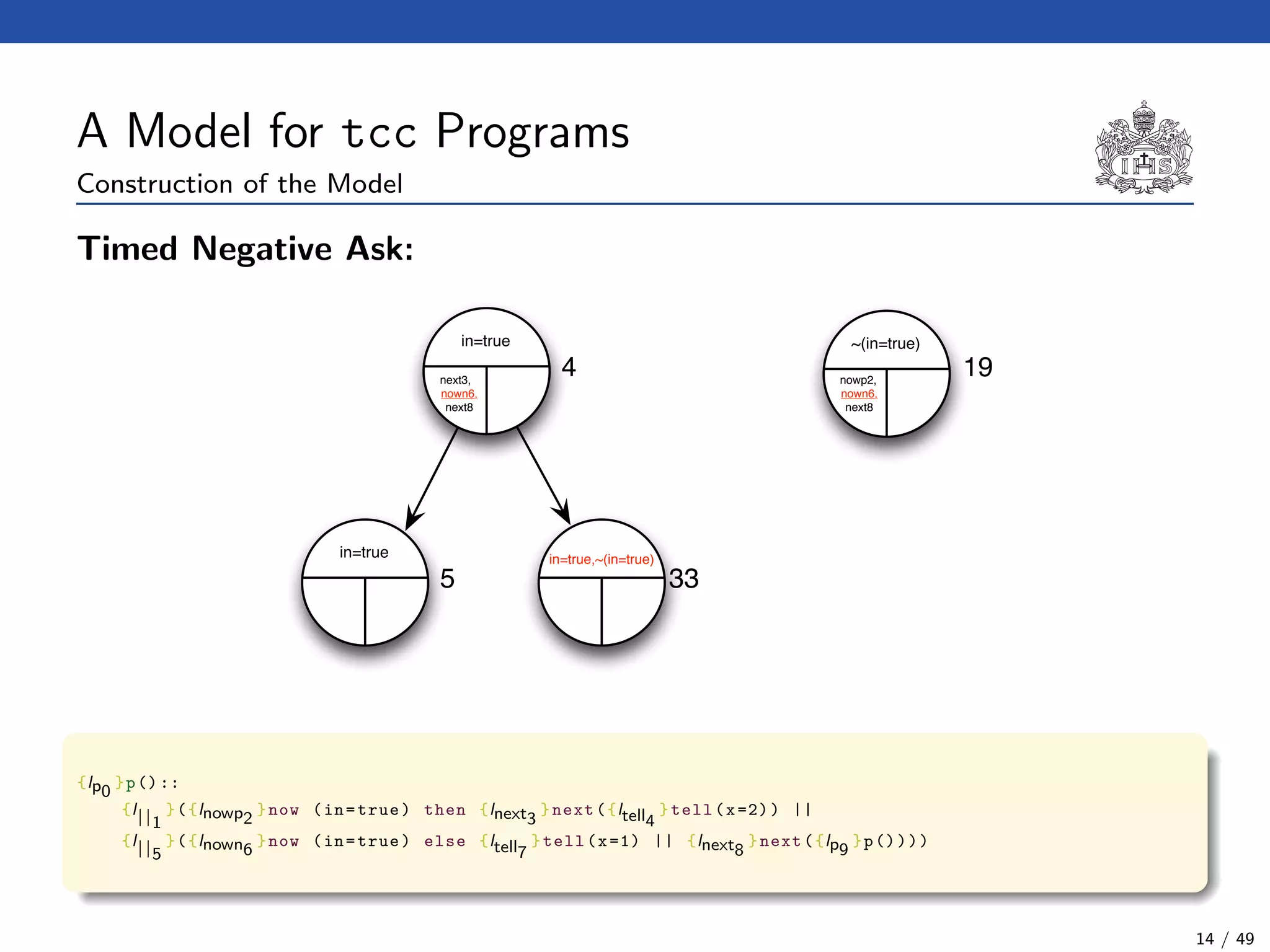
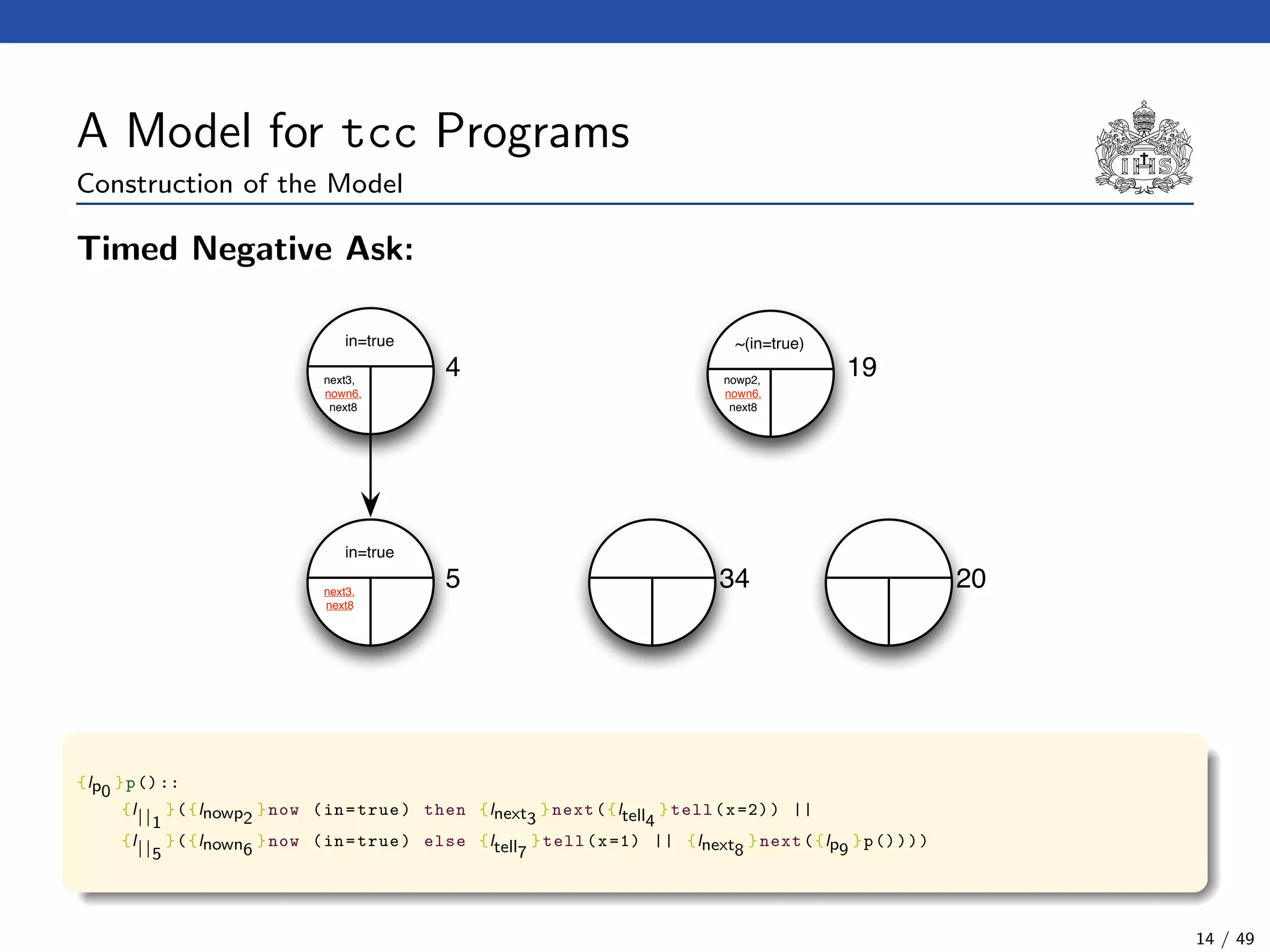
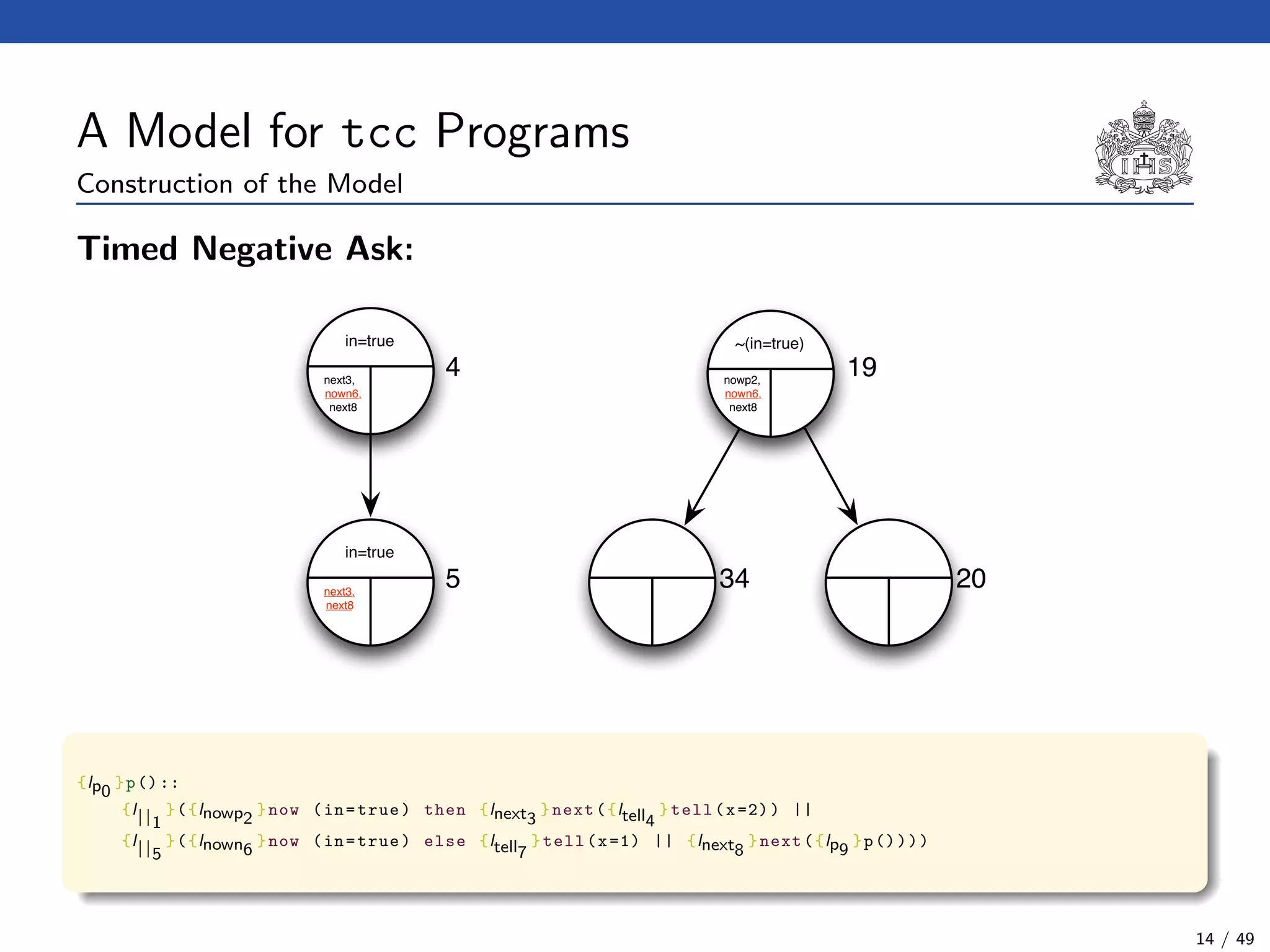
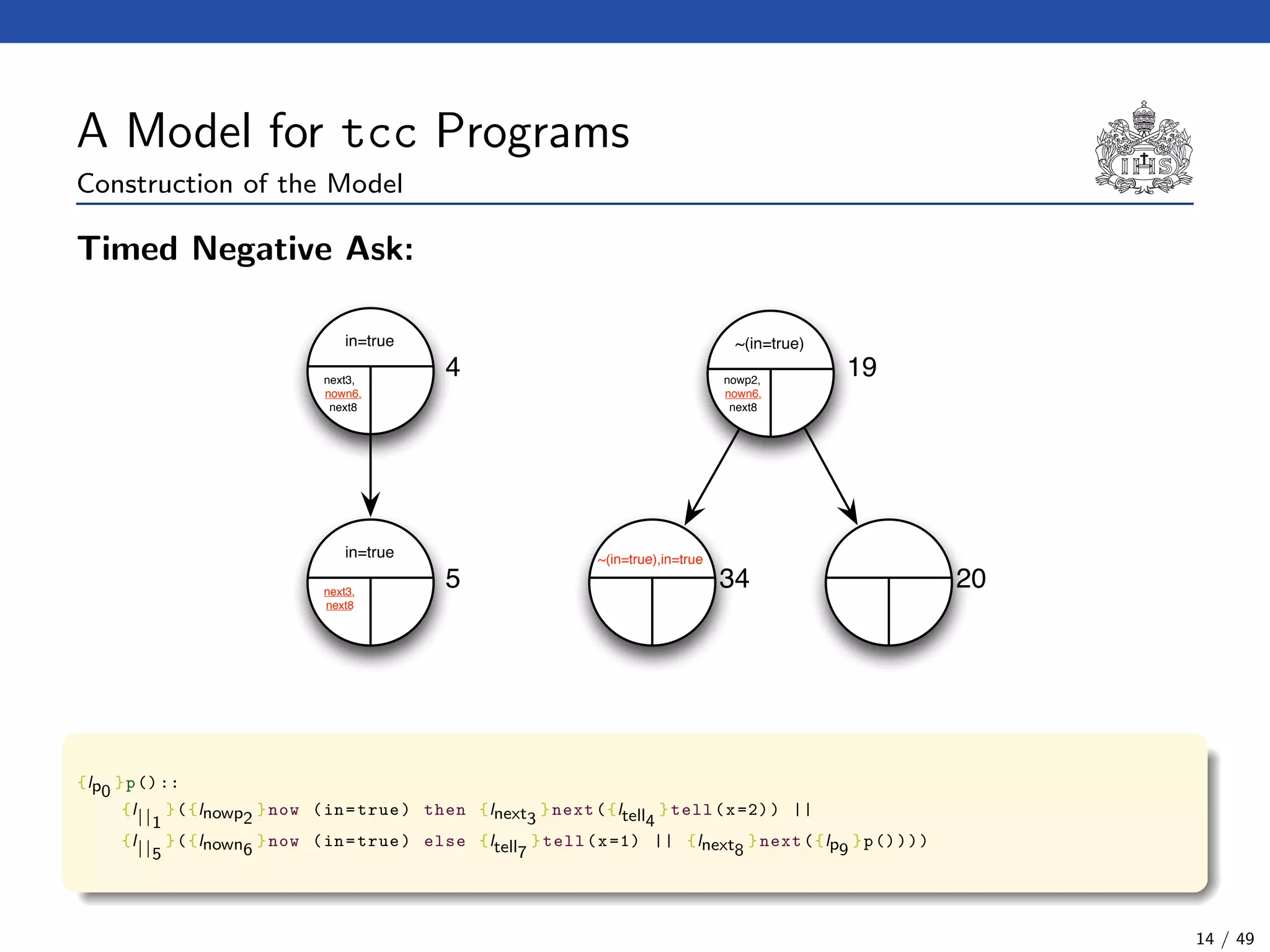
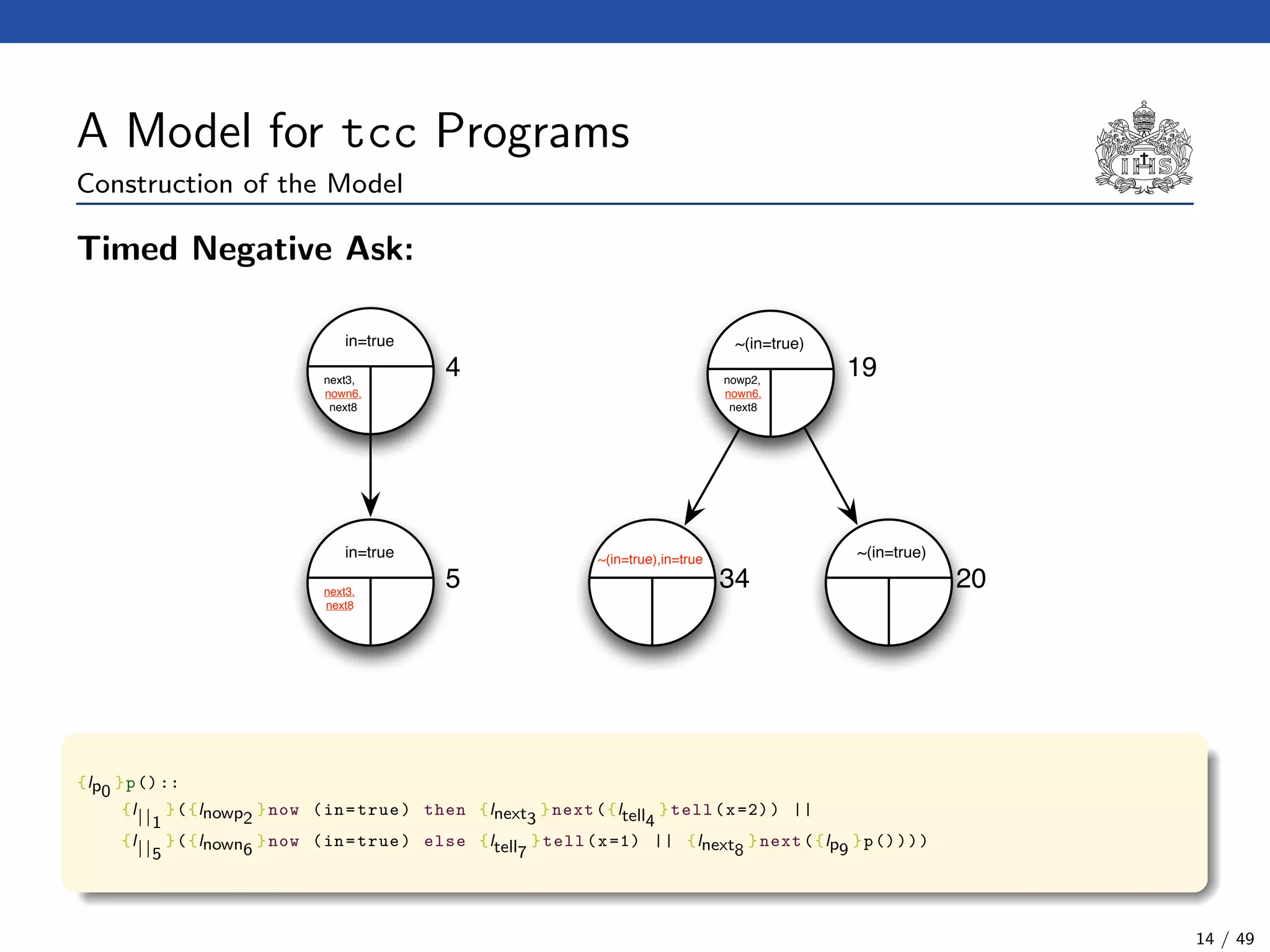
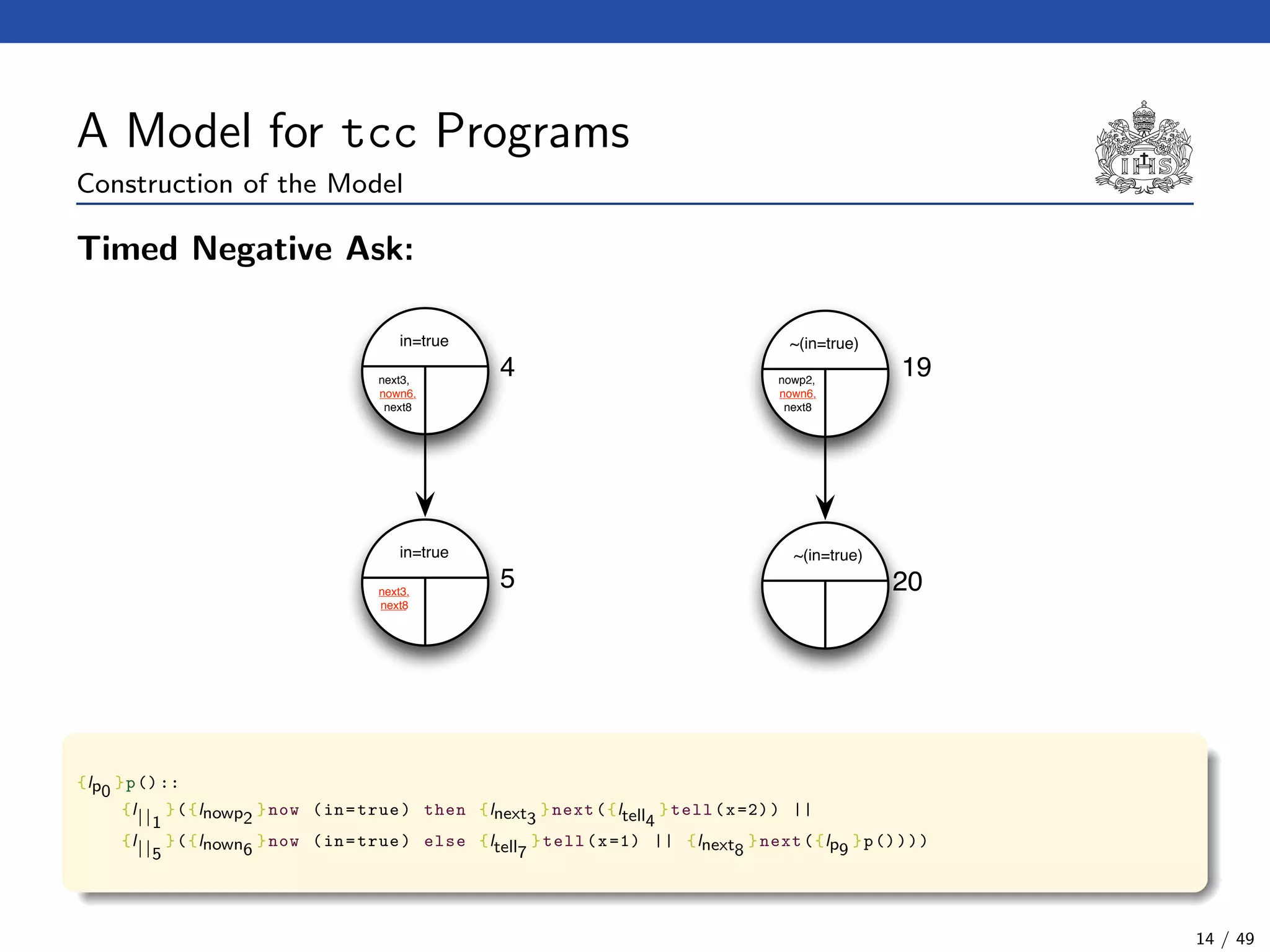
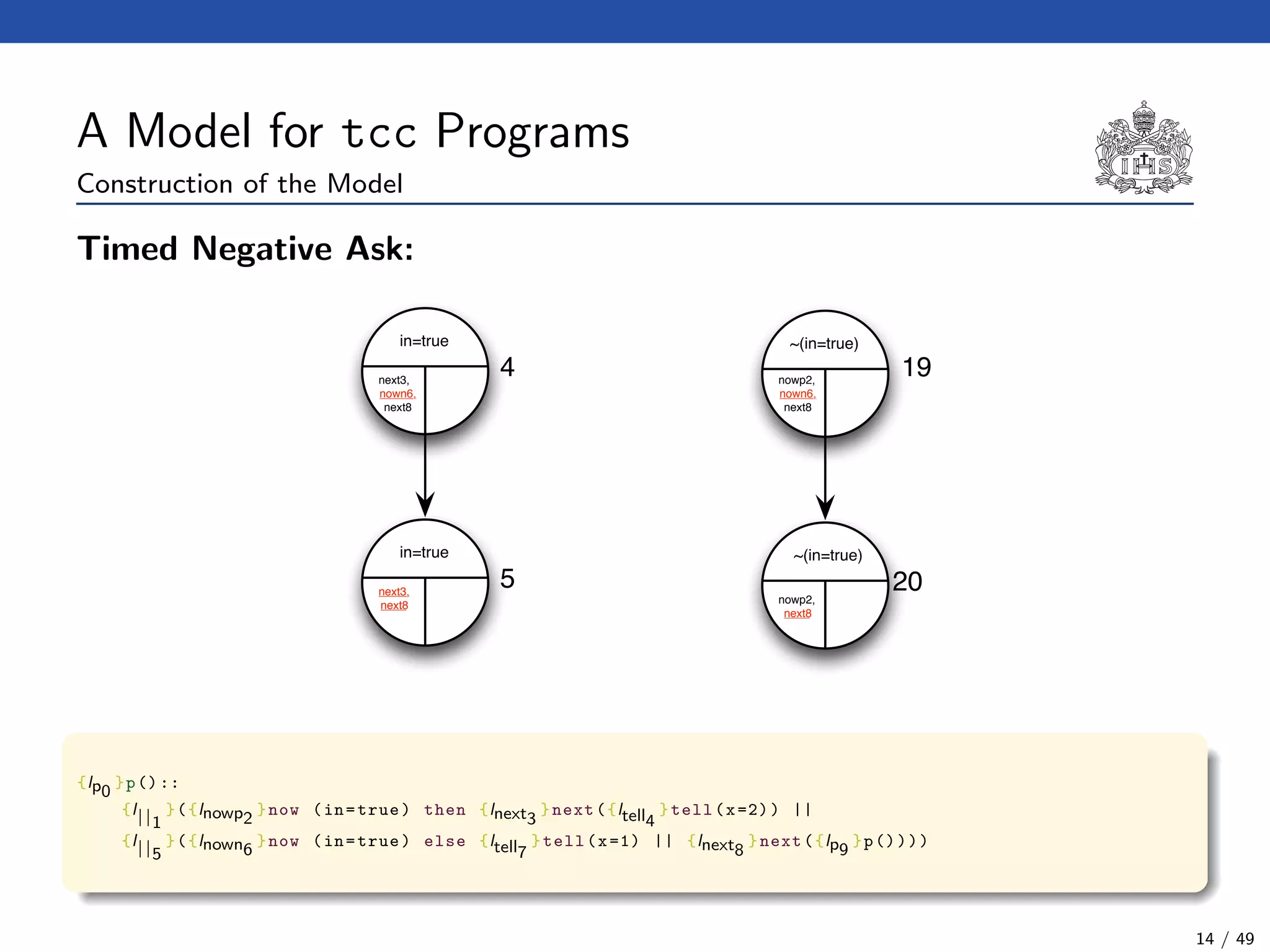
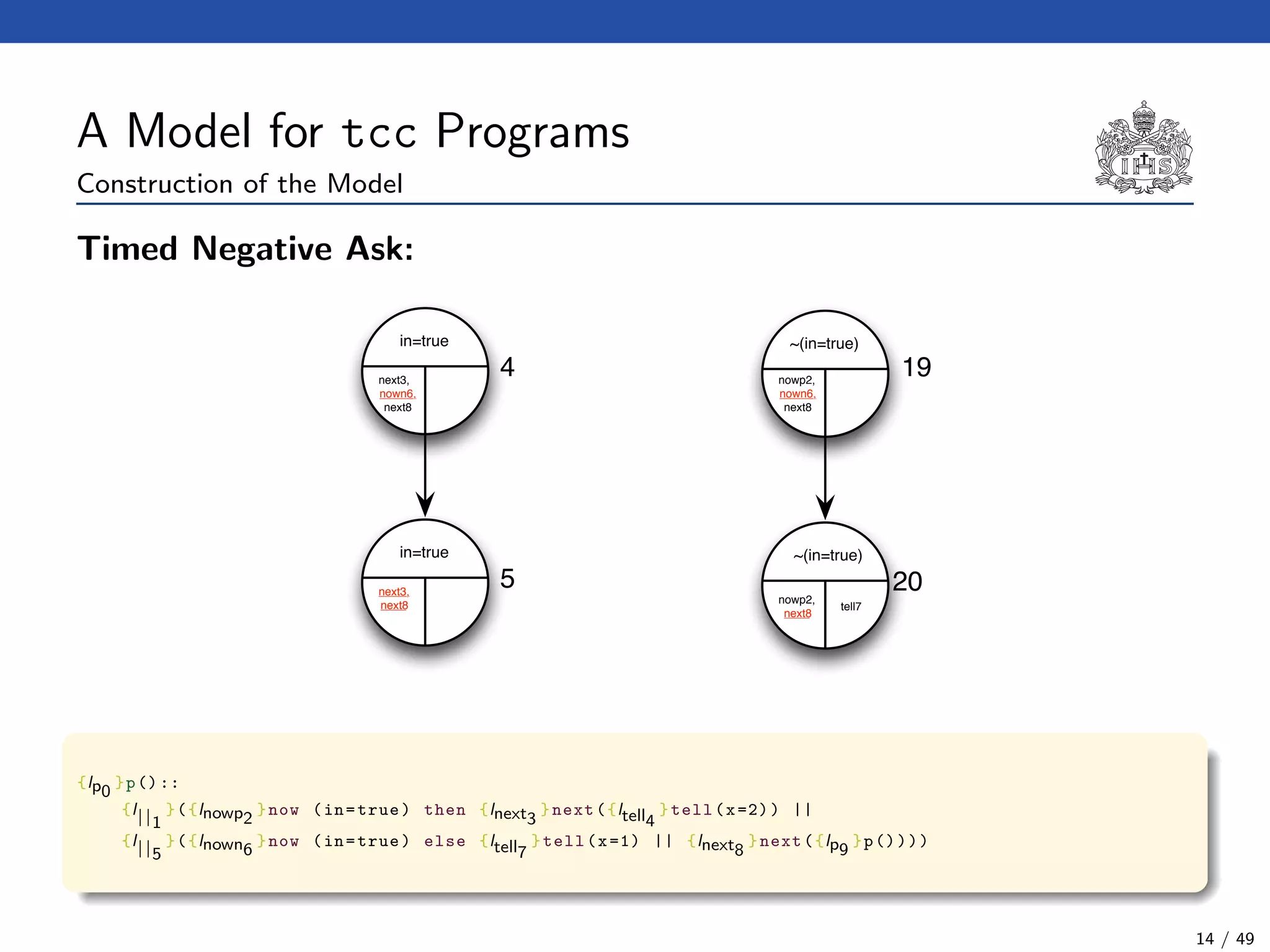
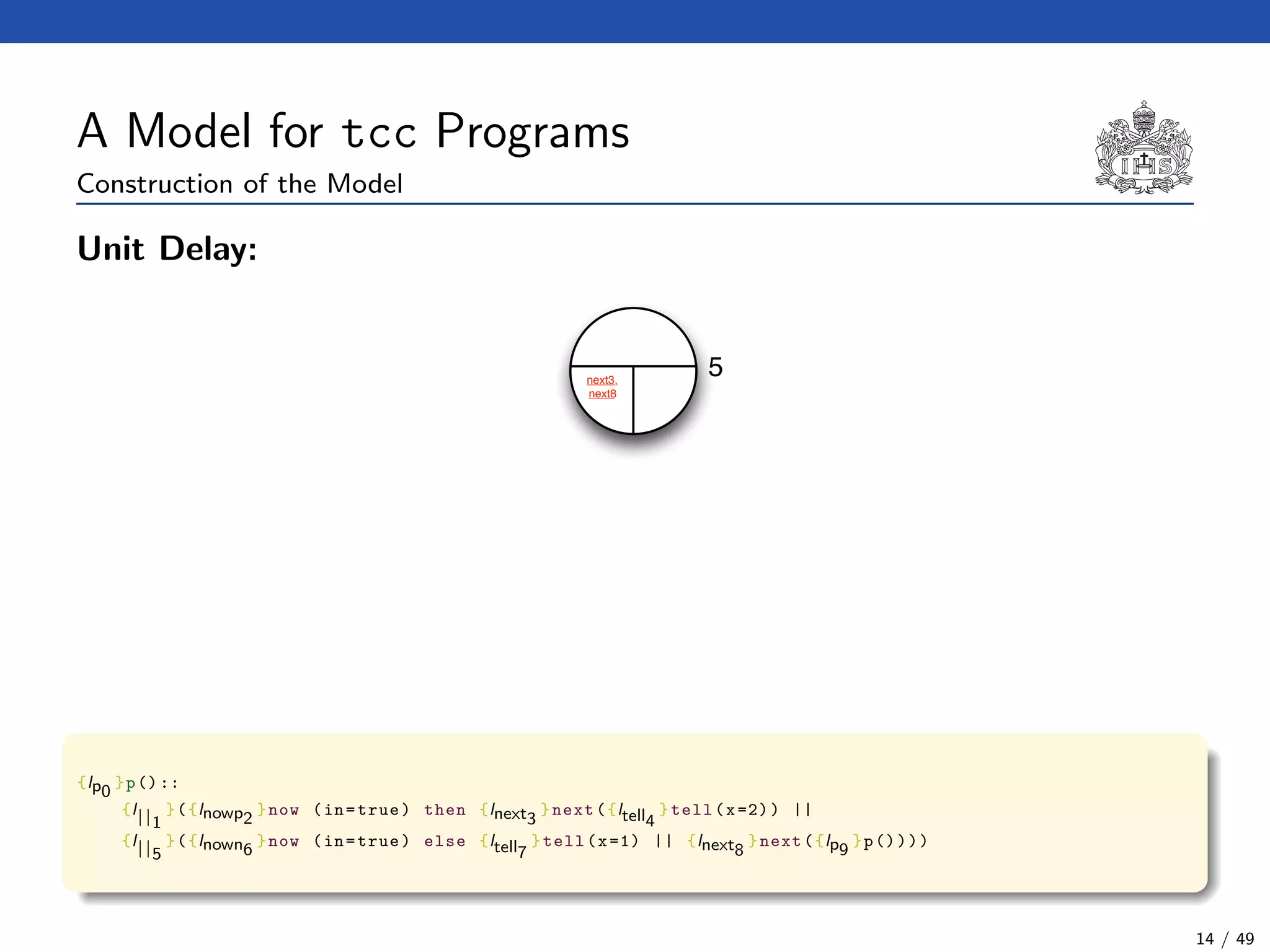
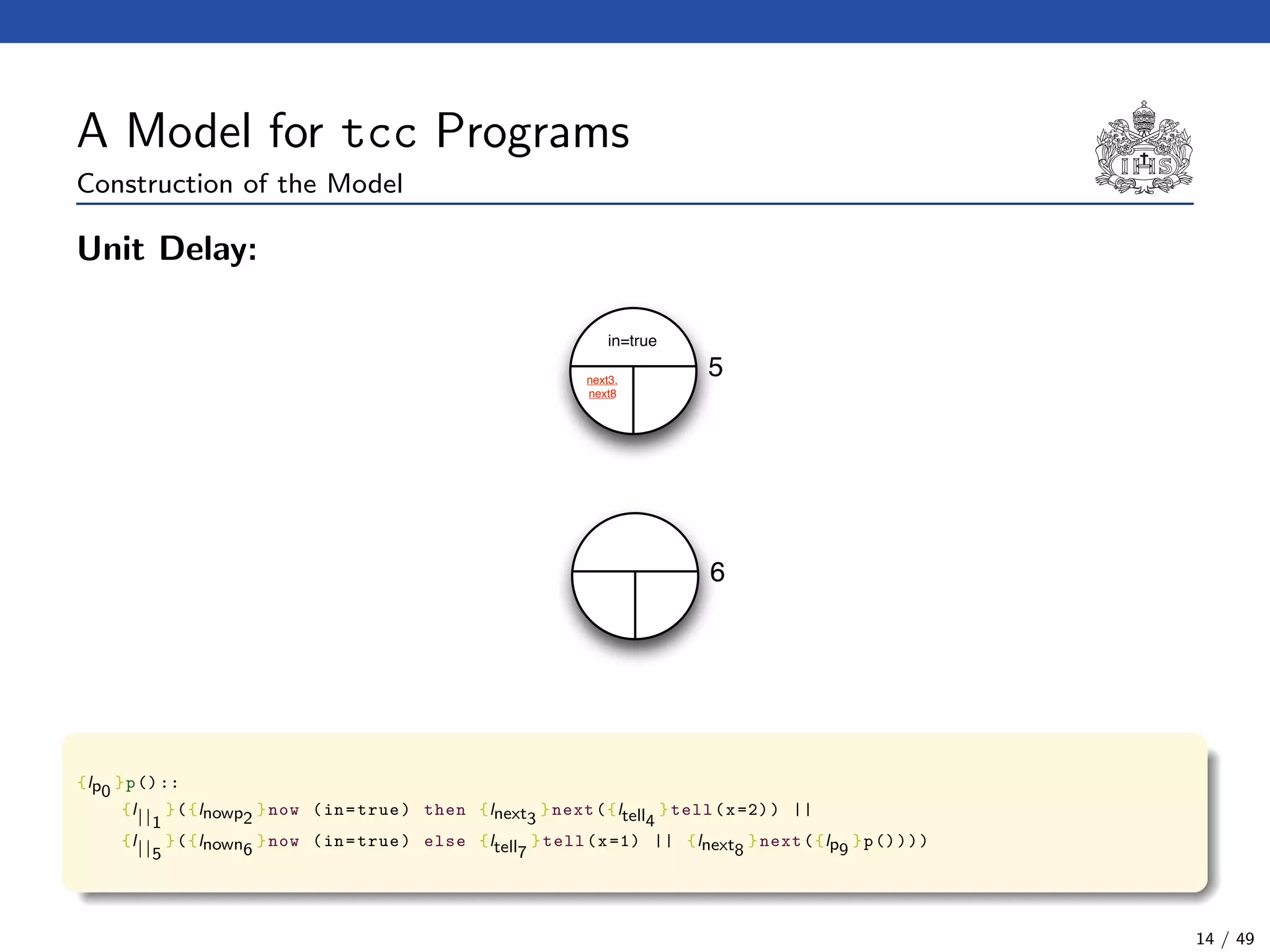
85. The tcc Calculus [SJG94]
Formal Syntax
(Agents) A ::= c (Tell)
| now c then A (Timed Positive Ask)
| now c else A (Timed Negative Ask)
| next A (Unit Delay)
| abort (Abort)
| skip (Skip)
| A || A (Parallel Composition)
| ∃x(A) (Hiding)
| g (Procedure Call)
(Procedure Calls) g ::= p(t1, . . . , tn)
(Declarations) D ::= g :: A (Definition)
| D.D (Conjunction)
(Programs) P ::= D.A
Return
32 / 49

86. The tcc Calculus [SJG94]
Formal Operational Semantics
Axioms for →. The binary relation → on configurations is the least relation satisfying the
rules :
(?, skip) → ?
(?, abort) → abort
(?, A || B) → (?, A, B)
(?, ∃x(A)) → (?, A[y/x]) (y not free in ?)
(?, p(t1, . . . , tn)) → (?, A[x1 → t1, . . . , xn → tn])
σ(?) c
(?, now c then A) → (?, A)
σ(?) c
(?, now c else B) → ?
Axioms for . The binary relation is the least relation satisfying the single rule :
∆, {now ci else Ai | i < n}
∆, {now ci else Ai | i < n}, {next Bj | j < m} {Ai | i < n}, {Bj | j < m}
Return
33 / 49

87. A Model for tcc Programs
Program Labeling
Let P be a tcc specification, the labeled version Pl of P is defined as follows.
The subindex k ∈ N corresponds to the number of labels introduced up to a
given point. When the labeling process starts, k = 0 and each time that we
introduce a new label, k is incremented by one.
• If P = tell c then Pl = {ltellk
} tell c.
• If P = now c then A then Pl = {lnowpk
} now c then Al .
• If P = now c else A then Pl = {lnownk
} now c else Al .
• If P = next A then Pl = {lnextk
} next Al .
• If P = skip then Pl = {lskipk
} skip.
• If P = A || B then Pl = {l||k
} (Al || Bl ).
• If P = p(t1, . . . , tn) then Pl = {lpk
} p(t1, . . . , tn).
Return
34 / 49

88. A Model for tcc Programs
The tcc Structure
Definition (tcc State)
Let AP be the atomic propositions in the tcc syntax and L be the set of all
labels generated during the labeling process described above. We define the
set of states as S ⊆ 2AP
× 2L
.
Definition (Equivalent States)
Given two tcc states s and s , we say that two states are equivalent if
1. the set of labels of s and s coincide, and
2. there exists a renaming γ of variables of the constraints in s which makes
them syntactically identical to the set of constraints of s .
Return
35 / 49

89. A Model for tcc Programs
Construction of the Model
Our procedure consists in locating an active label and perform the actions
associated with such agent. The process is performed while there are active
labels. When we reach a state where there is no active labels (quiescent
point) we have to pass to the next time unit, and then we continue with the
procedure. We represent this passage in our graph as follows:
1. Introduce a new node s related with s by a temporal transition. The
state s is a state where there is no active labels.
2. We introduce the temporal labels of s in the labels of s .
3. The store and the temporal labels of s are empty.
Return
36 / 49

90. A Model for tcc Programs
Construction of the Model
Tell S ≡ {ltellk
} tell c. The new information c is added to the
store in the current time. We translate this behavior to our
graph structure as follows:
1. Add a new node s related with the node s from which the
agent is execute.
2. The store of s is defined as the store of s plus the
constraint c (i.e. C(s ) = C(s) ∧ c).
3. The internal labels of s are obtained from those of s by
removing {ltellk
} (i.e. L(s ) = L(s){ltellk
}).
4. The temporal labels of s are the same as s (i.e.
LT(s ) = LT(s)).
Return
37 / 49

91. A Model for tcc Programs
Construction of the Model
Parallel S ≡ {l||k
} (Al || Bl ). The agents A and B are executed in
parallel. We translate this behavior to our graph structure as
follows:
1. Introduce a new node s related with the node s from
which the agent is execute.
2. The internal labels of s are obtained from those of s by
adding Al and Bl , and removing {l||k
}. Notice that this
corresponds to a concurrent semantics rather than an
interleaving interpretation of the parallel operator.
3. The store and the temporal labels of s are the same as s.
Return
38 / 49

92. A Model for tcc Programs
Construction of the Model
Timed Positive Ask S ≡ {lnowpk
} now c then Al . If the current store entails
c then the agent A is executed or does nothing otherwise.
Next we describe how to translate this agent to our graph.
1. Add two new nodes s1, s2 related with the node s from
which the agent is execute. This branch corresponds to
the two possible behaviors.
2. The store of s1 is defined as the union of the store of s
and the constraint c.
3. The store of s2 is defined as the store of s plus the
absence of the constraint c (i.e. C(s2) = C(s) ∧ ∼ c).
4. The internal labels of s1 are obtained from those of s by
adding Al and removing {lnowpk
}.
5. The internal labels of s2 are the same as s.
6. The temporal labels of s1 and s2 are the same as s.
Return
39 / 49

93. A Model for tcc Programs
Construction of the Model
Skip S ≡ {lskipk
} skip. This agent does nothing at every time
instant. We translate this agent to our graph as follows:
1. Construct a new node s related with the node s from
which the agent is executed.
2. The internal labels of s are obtained from those of s by
removing {lskipk
}.
3. The store and the temporal labels of s are the same as s.
Return
40 / 49

94. A Model for tcc Programs
Construction of the Model
Procedure Call S ≡ {lpk
} p(t1, . . . , tn). This operator refers to another
procedure which have different labels and variables. To
translate this agent to our graph we create a new node and
the label associated to the first agent of p is added to the
internal labels of the node.
Return
41 / 49

95. A Model for tcc Programs
Construction of the Model
Timed Negative Ask S ≡ {lnownk
} now c else Al . If on the quiescent point
the store does not entail c then the agent A is executed in
the next time instant, or does nothing otherwise. We
translate this behavior to our graph as follows:
1. Introduce two new nodes s1, s2 related with the node s
from which the agent is execute. This branch corresponds
to the two possible behaviors of the agent.
2. The store of s1 is defined as the union of the store of s
and the constraint c.
3. The store of s2 is defined as the store of s plus the
absence of the constraint c.
4. The internal labels of s1 and s2 are the same as s by
removing {lnownk
}.
5. The temporal labels of s1 are the same as s.
6. The temporal labels of s2 are obtained from those of s by
adding Al .
Return
42 / 49

96. A Model for tcc Programs
Construction of the Model
Unit Delay S ≡ {lnextk
} next Al . The agent A is executed in the next
time instant. We translate this agent to our graph as follows:
1. Construct a new node s related with the node s from
which the agent is execute.
2. The internal labels of s are the same as s but removing
{lnextk
}.
3. The temporal labels of s are obtained from those of s by
adding Al .
4. The store of s is the same as s.
Return
43 / 49

97. A Logic for the Specification of Properties
The ntcc Logic
Definition (CLTL Semantics)
We say that α ∈ Cω
satisfies (or that it is a model of) F in CLTL, written α CLTL F, iff
α, 1 CLTL F, where:
α, i CLTL ˙true
α, i CLTL ˙false
α, i CLTL c iff α(i) c
α, i CLTL ˙¬F iff α, i CLTL F
α, i CLTL F ˙∧ G iff α, i CLTL F and α, i CLTL G
α, i CLTL F ˙∨ G iff α, i CLTL F or α, i CLTL G
α, i CLTL ◦F iff α, i + 1 CLTL F
α, i CLTL F iff for all j ≥ i α, j CLTL F
α, i CLTL ♦F iff there is a j ≥ i s.t. α, j CLTL F
α, i CLTL
˙∃x F iff there is an x-variant α of α s.t. α , i CLTL F
Define F = {α | α CLTL F}. We say that F is CLTL valid iff F = Cω
, and that F is CLTL
satisfiable iff F = ∅.
Return
44 / 49

98. The Model Checking Algorithm
Closure
The closure of a formula ϕ, CL(ϕ), is the smallest set of formulas satisfying the
following conditions:
1. ϕ ∈ CL(ϕ),
2. ˙¬ϕ1 ∈ CL(ϕ), iff ϕ1 ∈ CL(ϕ),
3. if ϕ1 ˙∧ϕ2 ∈ CL(ϕ), then ϕ1, ϕ2 ∈ CL(ϕ),
4. if ϕ1 ˙∨ϕ2 ∈ CL(ϕ), then ϕ1, ϕ2 ∈ CL(ϕ),
5. if ˙∃x ϕ1 ∈ CL(ϕ), then ϕ1 ∈ CL(ϕ),
6. if ◦ϕ1 ∈ CL(ϕ), then ϕ1 ∈ CL(ϕ),
7. if ˙¬ ◦ ϕ1 ∈ CL(ϕ), then ◦ ˙¬ϕ1 ∈ CL(ϕ),
8. if ϕ1 ∈ CL(ϕ), then ϕ1, ◦ ϕ1 ∈ CL(ϕ),
9. if ♦ϕ1 ∈ CL(ϕ), then ϕ1, ◦♦ϕ1 ∈ CL(ϕ)
Return
45 / 49

99. The Model Checking Algorithm
Model Checking Graph
Definition (Model-Checking Graph)
Let ϕ be a formula, CL(ϕ) be the closure of ϕ and Z the tcc Structure. A node n of the
model-checking graph is formed by a pair of the form (sn, Qn) where sn is a state of Z and Qn is a
subset of CL(ϕ) and the atomic propositions such that the following conditions are satisfied:
1. for every atomic proposition p, p ∈ Qn iff p ∈ C(sn),
2. for every ˙∃x ϕ1 ∈ CL(ϕ), ˙∃x ϕ1 ∈ Qn iff ˙∃x ϕ1 ∈ C(sn),
3. for every ϕ1 ∈ CL(ϕ), ϕ1 ∈ Qn iff ˙¬ϕ1 /∈ Qn,
4. for every ϕ1 ˙∧ϕ2 ∈ CL(ϕ), ϕ1 ˙∧ϕ2 ∈ Qn iff ϕ1 ∈ Qn and ϕ2 ∈ Qn,
5. for every ϕ1 ˙∨ϕ2 ∈ CL(ϕ), ϕ1 ˙∨ϕ2 ∈ Qn iff ϕ1 ∈ Qn or ϕ2 ∈ Qn,
6. for every ˙¬ ◦ ϕ1 ∈ CL(ϕ), ˙¬ ◦ ϕ1 ∈ Qn iff ◦ ˙¬ϕ1 ∈ Qn,
7. for every ϕ1 ∈ CL(ϕ), ϕ1 ∈ Qn iff ϕ1 ∈ Qn and ◦ ϕ1 ∈ Qn,
8. for every ♦ϕ1 ∈ CL(ϕ), ♦ϕ1 ∈ Qn iff ϕ1 ∈ Qn or ◦ ♦ϕ1 ∈ Qn.
An edge in the graph is defined as follows: there will be an edge from one node n1 = (s1, Q1) to
another node n2 = (s2, Q2) iff there is an arc from the node s1 to the node s2 in Z and for every
formula ◦ϕ1 ∈ CL(ϕ), ◦ϕ1 ∈ Q1 iff ϕ1 ∈ Q2. This means that the next state s2 must satisfy φ if s1
satisfies ◦φ.
Return
46 / 49

100. A Prototypical Tool
Closure
CL(¬ϕ) = {♦((in = true) ˙∧ ˙¬ ◦ (x = 1)),
˙¬♦((in = true) ˙∧ ˙¬ ◦ (x = 1)),
◦ ♦((in = true) ˙∧ ˙¬ ◦ (x = 1)),
˙¬ ◦ ♦((in = true) ˙∧ ˙¬ ◦ (x = 1)),
◦ ˙¬♦((in = true) ˙∧ ˙¬ ◦ (x = 1)),
(in = true) ˙∧ ˙¬ ◦ (x = 1),
˙¬((in = true) ˙∧ ˙¬ ◦ (x = 1)),
˙¬ ◦ (x = 1), ◦ ˙¬(x = 1),
◦ (x = 1), (x = 1), ˙¬(x = 1),
(in = true), ˙¬(in = true)
}
Return
47 / 49

101. A Prototypical Tool
Model Checking Graph
s3 State
s2 State
s1 State
n1
n2
n3
n4
n5
n6
n7
n8
n9
n10
n12
n13
n14
n15
n16
s4 State
n17
n18
n19
n20
n21
n22
n23
n24
s5 State
n25
n26
n27
n28
s6 State
n29
n30
n31
n32
n11
Return
48 / 49

102. A Prototypical Tool
Strongly Connected Components
s3 State
s2 State
s1 State
n3
n7
n13
s4 State
n17
n21
s5 State
n27
s6 State
n29
n11
Self-Fulfilling SCC
Return
49 / 49