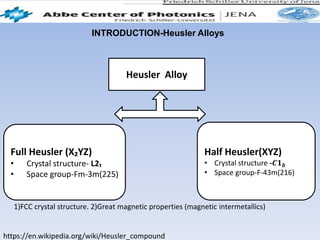
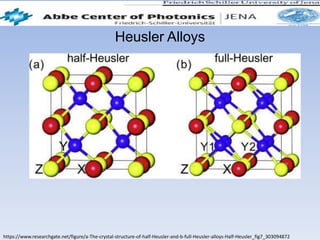
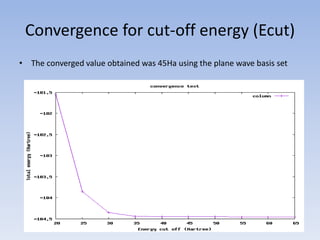
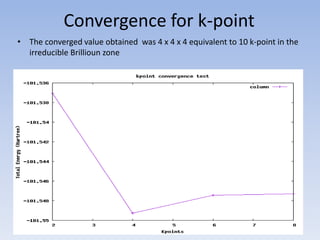
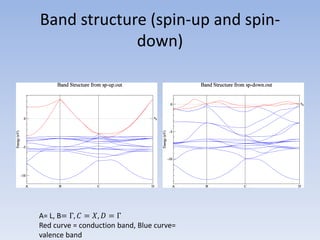
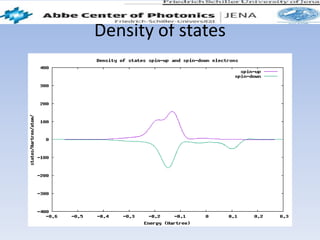
This document summarizes a first principles study of the electronic and magnetic properties of the MnAlCu2 Heusler compound. The author performed density functional theory calculations using the local density approximation (LDA) and generalized gradient approximation (GGA) to determine the material's lattice constant, band structure, density of states, and magnetic moment. The LDA results agreed well with literature GGA values, with small discrepancies of less than 2% for lattice constant and magnetic moment. The calculations achieved convergence for cut-off energy and k-point sampling. The MnAlCu2 compound showed potential for spintronic applications due to its spin polarization properties.

1. First principle study of the Electronic and
Magnetic properties of MnAlCu2 Heusler
compound
By
Ogunmoye Kehinde Adedapo
Matric No: 175627
Abbe School of photonics (ASP), Jena

2. INTRODUCTION-Heusler Alloys
Heusler Alloy
Full Heusler (X₂YZ)
• Crystal structure- L2₁
• Space group-Fm-3m(225)
Half Heusler(XYZ)
• Crystal structure -𝑪𝟏 𝒃
• Space group-F-43m(216)
https://en.wikipedia.org/wiki/Heusler_compound
1)FCC crystal structure. 2)Great magnetic properties (magnetic intermetallics)

3. Heusler Alloys
https://www.researchgate.net/figure/a-The-crystal-structure-of-half-Heusler-and-b-full-Heusler-alloys-Half-Heusler_fig7_303094872

4. Motivation
• To understand how the electronic and magnetic
properties of Heusler alloys are exploited for spintronic
applications .
• To compare variations in calculations done with LDA and
the GGA (literature)

5. Theoretical Method
• Total energy for DFT is given as
𝐸 = 𝑇𝑠 + 𝑑3 𝑟 𝑉𝑒𝑥𝑡 (𝑟) n(r) + 𝐸 𝐻𝑎𝑟𝑡𝑟𝑒𝑒 + 𝐸 𝑥 + 𝐸𝑐 (1)
Where 𝐸 𝑥[𝑛] and 𝐸𝑐[𝑛] are exchange and correlation energy deduced from
Kohn-Sham theory.
LOCAL DENSITY APPROXIMATION (LDA)
• The XC energy of Kohn and Sham is given as
𝐸 𝑥𝑐
𝐿𝐷𝐴
= 𝑑3
r n(r)𝑒 𝑥𝑐
𝐻𝐸𝐺
𝑛 𝒓 (𝟐)
Where 𝑒 𝑥𝑐
𝐻𝐸𝐺
(𝑛) is the exchange-correlation energy per unit particle. It is a
function of n.
The exchange part of 𝑒 𝐻𝐸𝐺 is given as
• 𝑒 𝑥
𝐻𝐸𝐺 = −
3
4
(
3
2𝜋
)
2
3
1
𝑟𝑠
(3)
Miguel A.L Marques, Functionals in DFT (2012)

6. Theoretical method
• 𝑟𝑠 is the Wgner-seitz radius given as
• 𝑟𝑠 = (
3
4𝜋𝑛
)
1
3 (4)
• SLATER-PAULING RULE
• shows relationship between the magnetic moment (𝑀 𝑚) and number of
valence electrons (𝑁𝑣)
• 𝑀 𝑚 = 𝑁𝑣 − 2𝑛↓ (5)
• 2𝑛↓ is the number of electrons in the minority state with minimum of 3 in
the d minority band
• 𝑀 𝑚 = 𝑁𝑣 − 6 (6)
• For full Heusler , there 4 atoms in each unit cell, therefore we have that
• 𝑀 𝑚 = 𝑁𝑣 − 24 (7)
Graf T., Felser C., Parkin S.S.P. (2015) Heusler Compounds: Applications in Spintronics. In: Xu Y., Awschalom D., Nitta J. (eds)
Handbook of Spintronics. Springer, Dordrecht

7. Results and discussion
• The LDA result shows a good agreement with the GGA with an
overestimation of 0.6% and 0.03% respectively.
• For the Broadening factor, I obtained a converged value of
0.04Ha
LDA(My work) GGA(literature)
LATTICE CONSTANT
(Å)
5.959 5.922 [1]
5.957 [2]
[1] https://materialsproject.org/materials/mp-905565/
[2] D.P Rai and R.K Thapa, Journal of Alloys and compounds 612 (2014) 355-360

8. Convergence for cut-off energy (Ecut)
• The converged value obtained was 45Ha using the plane wave basis set

9. Convergence for k-point
• The converged value obtained was 4 х 4 х 4 equivalent to 10 k-point in the
irreducible Brillioun zone

10. Atomic structure
• The atomic structure was visualized using cut3d.
• Cu- Blue, Mn- Red, Al- Gray
a

11. Band structure (spin-up and spin-
down)
A= L, B= Γ, 𝐶 = 𝑋, 𝐷 = Γ
Red curve = conduction band, Blue curve=
valence band

12. Density of states

13. Magnetic moment
• The magnetic moment obtained by LDA is in good agreement with the
GGA with errors of +1.2% and -0.7% respectively
LDA (My work) GGA (literature)
TOTAL MAGNETIC
MOMENT (μB)
3.542 3.500 [1]
3.568 [2]
1] https://materialsproject.org/materials/mp-905565/
[2] D.P Rai and R.K Thapa, Journal of Alloys and compounds 612 (2014) 355-360

14. Conclusion and outlook
• Disparity between LDA and GGA calculations for lattice parameter and
magnetic moment not up to 2%.
• Spin polarization in Heusler compound is a key ingredient for spintronic
applications
• Convergence was achieved for the parameters used for calculations.
• For the Magnetic moment each Mn atom contributed to the bulk of the
total magnetic moment (3.995μ𝐵)
• Given more time I would look into the optical and elastic properties .