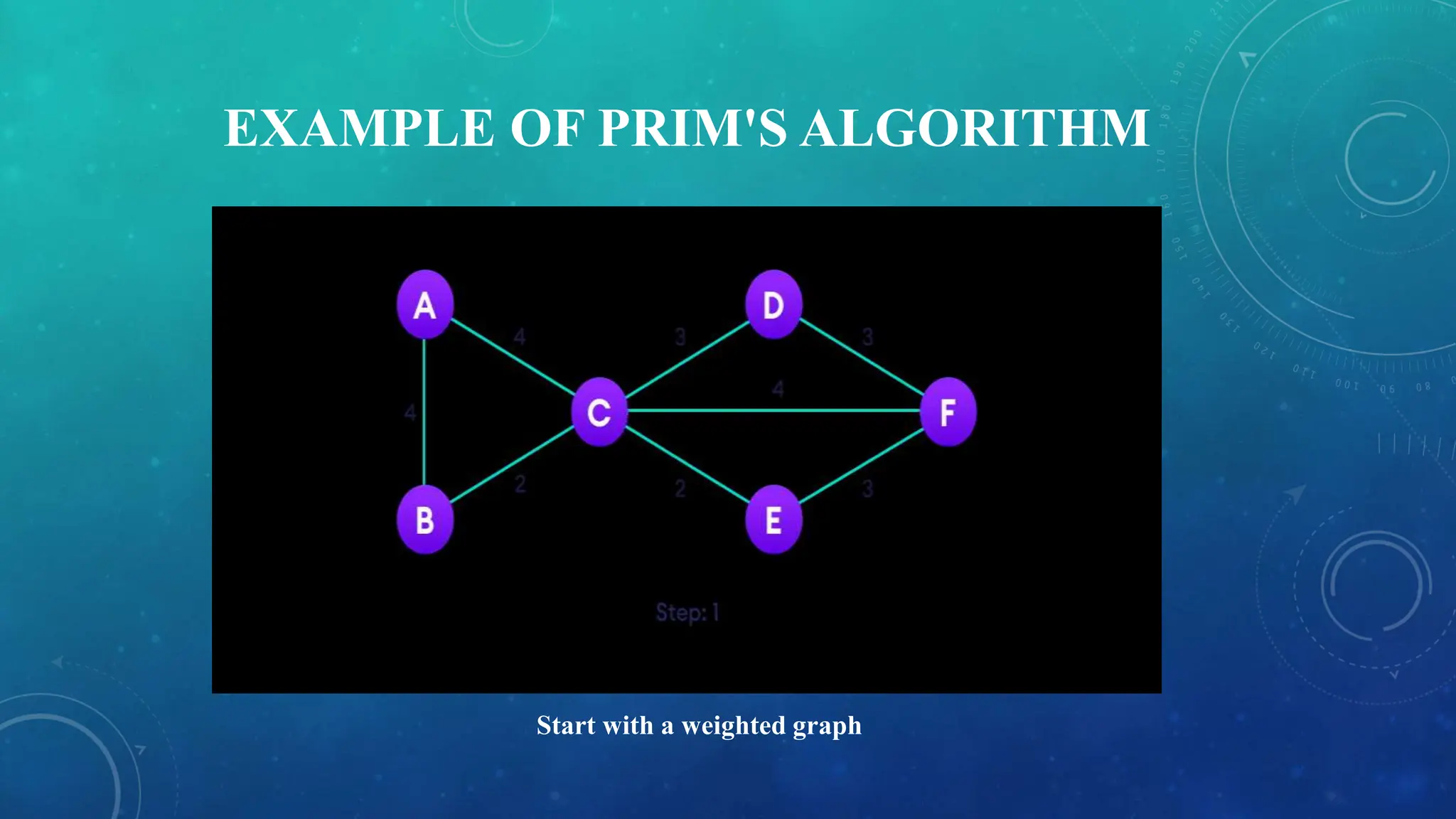
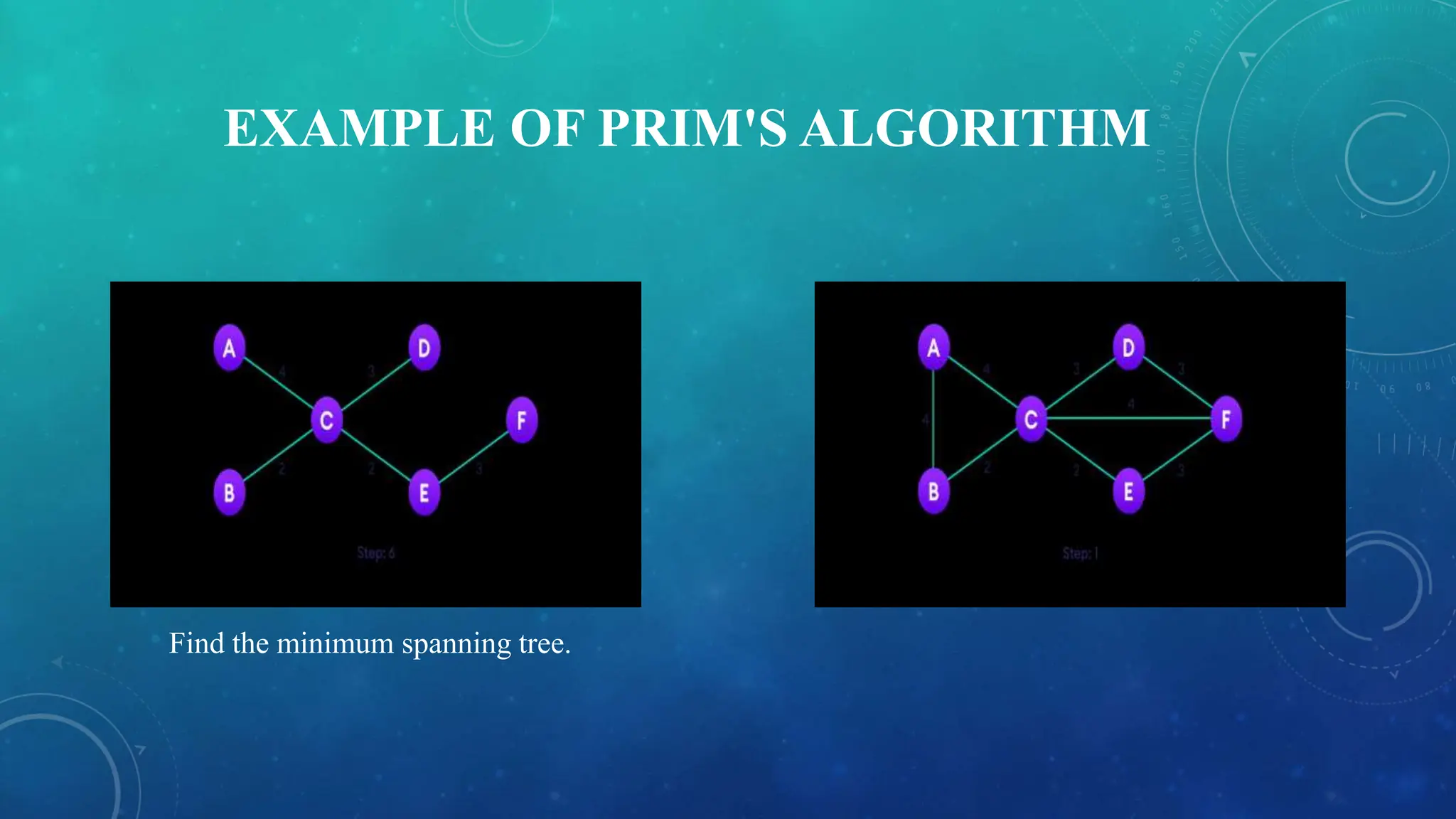
This presentation summarizes minimum spanning tree algorithms. It defines undirected and connected graphs, and explains that a minimum spanning tree is a spanning tree that connects all vertices of a graph using the minimum total edge weight. Prim's algorithm and Kruskal's algorithm are described as approaches to find the minimum spanning tree. Prim's algorithm is explained in more detail, with the steps including initializing the tree with a random vertex, then repeatedly adding the lowest weight edge connecting the tree to a new vertex until all vertices are included. An example demonstrates how Prim's algorithm is applied to a weighted graph to find the minimum spanning tree.

1. WELCOME TO MY
PRESENTATION

2. Md. Harun Or Rashid
ID: 193-15-2966
PC-A

3. PRESENTATION TOPIC
Minimum Spanning Tree

4. WHAT IS SPANNING TREE?
• Before we learn about spanning trees, we need to understand two
graphs: undirected graphs and connected graphs.
1. Undirected Graph: An undirected graph is a graph in which the
edges do not point in any direction (ie. the edges are bidirectional).
2. Connected Graph: A connected graph is a graph in which there is
always a path from a vertex to any other vertex.
• Spinning Tree: A spanning tree is a sub-graph of an undirected
connected graph, which includes all the vertices of the graph with a
minimum possible number of edges.

5. WHAT IS MINIMUM SPANNING TREE?
• Minimum Spanning Tree: A minimum spanning tree is a spanning tree
in which the sum of the weight of the edges is as minimum as possible.
• The minimum spanning tree from a graph is found using the following
algorithms:
1. Prim’s Algorithms.
2. Kruskal’s Algorithms.

6. PRIM’S ALGORITHM
Prim's algorithm is a minimum spanning tree algorithm that finds the
subset of the edges of that graph which
• form a tree that includes every vertex.
• has the minimum sum of weights among all the trees that can be
formed from the graph.

7. HOW PRIM'S ALGORITHM WORKS
• We start from one vertex and keep adding edges with the lowest
weight until we reach our goal.
• The steps for implementing Prim's algorithm are as follows:
1.Initialize the minimum spanning tree with a vertex chosen at
random.
2.Find all the edges that connect the tree to new vertices, find the
minimum and add it to the tree
3.Keep repeating step 2 until we get a minimum spanning tree

8. EXAMPLE OF PRIM'S ALGORITHM
Start with a weighted graph

9. EXAMPLE OF PRIM'S ALGORITHM
Choose a vertex

10. EXAMPLE OF PRIM'S ALGORITHM
Choose the shortest edge from this vertex
and add it.

11. EXAMPLE OF PRIM'S ALGORITHM
Choose the nearest vertex not yet in the
solution.

12. EXAMPLE OF PRIM'S ALGORITHM
Choose the nearest edge not yet in the
solution, if there are multiple choices,
choose one at random.

13. EXAMPLE OF PRIM'S ALGORITHM
Find the minimum spanning tree.

14. MINIMUM CONNECTOR ALGORITHMS
Kruskal’s Algorithm Prim’s Algorithm
Se

16. THANK YOU