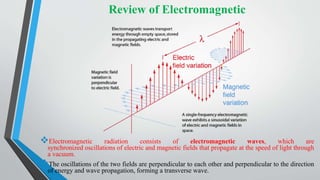
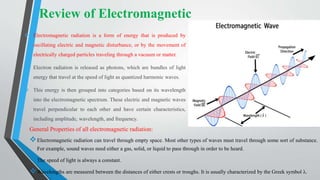
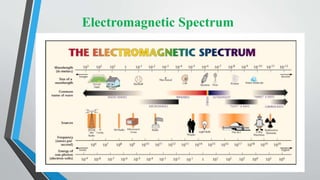
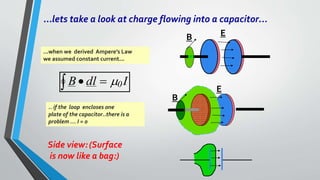
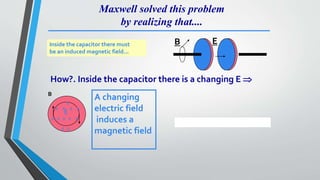
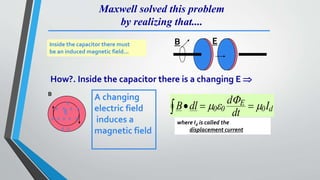
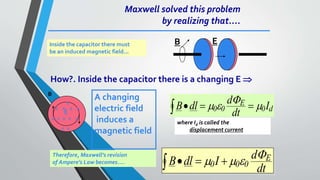
Microwave engineering pertains to the study and design of microwave circuits, components, and systems operating between 300 MHz and 300 GHz. Some key topics covered in the document include the fundamental principles of microwave engineering, common applications like radar and wireless transmission, properties of microwaves like their ability to support larger bandwidths, and Maxwell's equations which describe how electric and magnetic fields propagate and interact to form electromagnetic waves. During World War II, microwave engineering played an important role in developing radar to detect enemy ships and planes.