The document contains two calculus word problems and their solutions. The first problem asks at what time the temperature of a pool is highest based on a temperature model, and the answer is 4PM. The second problem asks how long the timer should be set on a camera to take a picture of someone zip lining halfway through their ride, and the answer is 44 seconds. Both problems involve taking derivatives or integrals of functions to find maximums/minimums or distances traveled over time.

1. The Awesomest Calculus PowerPoint EVER!!! By Meghan Almaas

2. Derivative Problem Jessica has a pool in her backyard and she likes to go swimming when it gets warm outside. However, due to a rare skin condition that prevents her from coming in contact with cold water, Jessica will only swim in her pool when the water is the warmest.

3. The temperature of the pool in degrees Fahrenheit over 12 hours starting at 10AM can be modeled by: y= .017x ³ – 1.046x ² + 20.349x – 41.385 At what time, rounded to the nearest hour, is the temperature the highest so that Jessica can go swimming?

4. Solution Find the derivative of the function: y’= .051x ² – 2.092x + 20.349 Using the Quadratic Formula, solve for the zeros: x=2.092 ± (-2.092)² – 4(.051)(20.349) 2(.051)

5. The values of x are 25.163 and 15.857. Because 25.163 is outside the designated interval, you can eliminate that option. Now you must double check that 16 (nearest hour to 15.857 ) is truly a maximum!!

6. A maximum at 16 would require the derivative to change signs from positive to negative. Therefore, use 15 and 17 as points around 16 to discover if the sign changes. y’(15)=.444 (positive) y’(17)= -.476 (negative) With a change from + to –, 16 is the time when the pool is the warmest. Because 16 is 6 hours after 10AM , it can be converted to 4PM .

7. Integral Problem Sarah is in Hawaii with some friends and she wants to ride a zip line. However, one of her friends Cheyanne is too afraid to go on the zip line. She wants to take a picture of Sarah exactly half way between the ends of the zip line for her photography class. Her camera has a timer that can start as soon as Sarah starts her ride. In order to take a picture at the exact moment that Sarah has traveled half the distance, Cheyanne needs to know the time Sarah will reach it so she can set the timer.

8. The velocity of Sarah on the zip line can be modeled by v(t)=sint + t on the interval [0,6] where t=6 represents 60 sec. Using this information, find the time in seconds that Cheyanne should set her camera timer to capture Sarah at the moment she’s traveled half the distance of the zip line.

9. Solution Find the total distance of the zip line over the interval by integrating the velocity: (sint+t)dt = (-cost+ ½ t ²)] (-cos6+½(6²)) – (-cos0) = 18.04 6 6 0 0

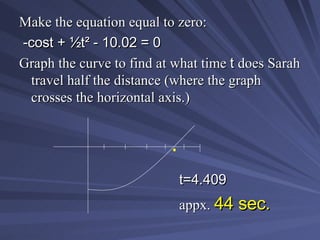
10. Using the total distance, solve for t when the distance is half through integration: (sint+t)dt = 18.04/2 (-cost + ½t²)] = 9.02 (-cost + ½t²) – (-cos0) = 9.02 -cost + ½t² - 1 = 9.02 0 t t 0

11. Make the equation equal to zero: -cost + ½t² - 10.02 = 0 Graph the curve to find at what time t does Sarah travel half the distance (where the graph crosses the horizontal axis.) t=4.409 appx. 44 sec. .