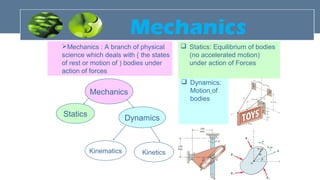
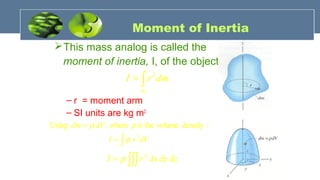
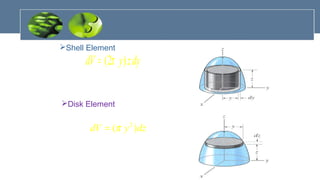
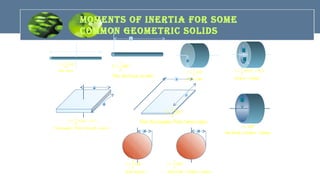
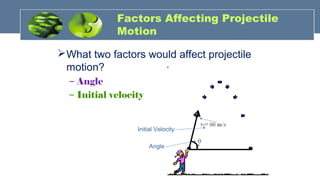
The document provides an overview of mechanics, including key concepts such as statics, dynamics, kinematics, and kinetics, as well as Newton's laws of motion that govern the behavior of objects. It discusses frictional forces, moment of inertia, radius of gyration, and projectile motion, detailing both their definitions and applications. The content is structured around group members' contributions, emphasizing fundamental principles and equations relevant to physics and engineering.

2. IntroductIon of
mechanIcs
Md. Asif Rahman (151-15-5090)

3. our Group members
Md. Asif Rahman (151-15-5090)
Mst. Keya (151-15-5136)
Mostake Ahmed Hero (151-15-5083)
Salma Siddika (151-15-4946)
Md. Zubayer Islam (151-15-5047)

4. Mechanics
Statics Dynamics
Kinematics Kinetics
Mechanics : A branch of physical
science which deals with ( the states
of rest or motion of ) bodies under
action of forces
 Dynamics:
Motion of
bodies
 Statics: Equilibrium of bodies
(no accelerated motion)
under action of Forces
Mechanics

5. Mechanics
Kinematics:- Description of motion and includes
consideration of time, displacement, velocity,
acceleration and space factors of a system‘s
motion
Kinetics:- Study of forces associated with the
motion of a body

6. prIncIpLes of
mechanIcs
Mst. Keya (151-15-5136)

7. neWton’s fIrst LaW
The study of rigid body mechanics is
formulated on the basis of Newton’s laws
of motion.
First Law:
An object at rest tends to stay at rest and an
object in motion tends to stay in motion with the
same speed and in the same direction, unless
acted upon by an unbalanced force.

8. neWton’s second LaW
Second Law:
The acceleration of a particle is proportional to
the vector sum of forces acting on it, and is in the
direction of this vector sum.
m
F

a

amF

=

9. NEWTON’S Third LAW
 Third Law:
The mutual forces of action and reaction between
two particles are equal in magnitude, opposite in
direction and collinear.
F
r
F−
rF
r
F−
r
Confusing? Point: Isolate the body
Forces always occur in pairs – equal
and opposite action-reaction force pairs.

10. 2
r
GMm
F =
- M & m are particle masses
- G is the universal constant of gravitation,
6.673 x 10-11
m3
/kg-s2
- r is the distance between the particles.
where
- m is the mass of the body in
question
- g = GM/R2
= 9.81 m/s2
(32.2
ft/s2)
m
M
W=mg
M
m
r
F
NEWTON’S GrAviTATiON LAW

11. FricTiONAL
FOrcE
Mostake Ahmed Hero (151-15-5083)

12. FricTiONAL FOrcES
PP
Frictional forces:Frictional forces: Frictional forces are parallel toFrictional forces are parallel to
the surfaces in contact and oppose motion orthe surfaces in contact and oppose motion or
impending motion.impending motion.
Two types of FrictionalTwo types of Frictional
force:force:
Static FrictionStatic Friction
Kinetic FrictionKinetic Friction

13. FricTiONAL FOrcE
Static Friction:. No
relative motion
Kinetic Friction:
Relative motion.
fk = µknfk = µknfs ≤ µsnfs ≤ µsn
Procedure for solution of equilibrium
problems is the same for each case:
0 0x yF FΣ = Σ =

14. dEpENdENcE OF FricTiON
 Nature of surface.
 Roughness of surface.
 Medium between two surface.
 Temperature.

15. impOrTANT pOiNTS TO cONSidEr WhEN SOLviNG
FricTiON prObLEmS
 The maximum force of static friction is theThe maximum force of static friction is the
force required to just start motion.force required to just start motion.
s sf nµ≤
n
fs
P
W
Equilibrium exists at that instant:Equilibrium exists at that instant:
0; 0x yF FΣ = Σ =

16. impOrTANT pOiNTS TO cONSidEr WhEN SOLviNG
FricTiON prObLEmS
• The force ofThe force of kinetic frictionkinetic friction is that force required tois that force required to
maintainmaintain constant motionconstant motion..
k kf nµ=
• Equilibrium exists if speed is constant, butEquilibrium exists if speed is constant, but ffkk
doesdoes notnot get larger as the speed is increased.get larger as the speed is increased.
0; 0x yF FΣ = Σ =
n
fk
P
W

17. Moment of Inertia &
Radius of Gyration
Salma Siddika (151-15-4946)

18. Moment of Inertia of a body.
Radius of Gyration.
Moment of Inertia of Composite
Bodies.
MoMent of InertIa &
radIus of GyratIon

19. Moment of Inertia
This mass analog is called the
moment of inertia, I, of the object
– r = moment arm
– SI units are kg m2
∫=
m
dmrI 2
∫∫∫= dzdydxrI 2
ρ
dVrI
dVdm
∫=
=
2
:densityvolumetheiswhere,Using
ρ
ρρ

20. Shell Element
Disk Element
dyzydV )2( π=
dzydV )( 2
π=

21. RodThin
12
1 2
MLI =
end)at(axisRodThin
3
1 2
MLI =
L
DiskSolid
2
1 2
MRI =
R
CylinderHollow
)(
2
1 2
2
2
1 RRMI +=
R2
R2
CylinderHollowdThin Walle
2
MRI =
R
a
b
center)(throughPlaterRectangula
)(
12
1 22
baMI +=
a
b
edge)(aboutPlaterRectangulaThin
3
1 2
MaI =
SphereSolid
5
2 2
MRI =
R
SphereHollowdThin Walle
3
2 2
MRI =
R
MoMents of InertIa for soMe
coMMon GeoMetrIc solIds

22. radIus of GyratIon
radIus of GyratIon: Frequently tabulated data
related to moments of inertia will be presented
in terms of radius of gyration.
m
I
kormkI == 2

23. MoMent of InertIa of
coMposIte bodIes
1. Divide the composite area into simple body.
2. Compute the moment of inertia of each simple body
about its centroidal axis from table.
3. Transfer each centroidal moment of inertia to a
parallel reference axis
4. The sum of the moments of inertia for each simple
body about the parallel reference axis is the moment
of inertia of the composite body.
5. Any cutout area has must be assigned a negative
moment; all others are considered positive.

24. projectIle
MotIon
Md. Zubayer Islam (151-15-5047)

25. What is Projectile
Motion?
PROJECTILE MOTION: when an object is
thrown obliquely into space it’s called a
projectile and its motion is called
projectile motion.

26. Types of Projectile Motion
 HORIzONTaL-
– Motion of a ball rolling freely
along a level surface
– Horizontal velocity is ALWAYS
constant
 VERTICaL-
– Motion of a freely falling object
– Force due to gravity
– Vertical component of velocity
changes with time
 PaRabOLIC-
– Path traced by an object
accelerating only in the vertical
direction while moving at
constant horizontal velocity

27. ExaMPLEs Of PROJECTILE MOTION
Projectile motion applies to
sports-
Projectile motion applies to destructive
projectiles

28. Equations
 X- Component
 Y- Component
 Vectors
tvxx xiif +=
gtvv
ygvv
gttvyy
yiyf
yiyf
yiif
−=
∆−=
−+=
2
2
1
22
2
)sin(
)cos(
θ
θ
iyi
ixi
vv
vv
=
=
Note: g= 9.8
m/s^2

29. Factors Affecting Projectile
Motion
What two factors would affect projectile
motion?
– Angle
– Initial velocity
Initial Velocity
Angle

30. CONCLusION Of PROJECTILE
MOTION
A projectile is any object upon which the only force is gravity.
Projectiles travel with a parabolic trajectory due to the
influence of gravity.
There are no horizontal forces acting upon projectiles and
thus no horizontal acceleration.
The horizontal velocity of a projectile is constant. there is a
vertical acceleration caused by gravity 9.8 m/s.
The horizontal motion of a projectile is independent of its
vertical motion.