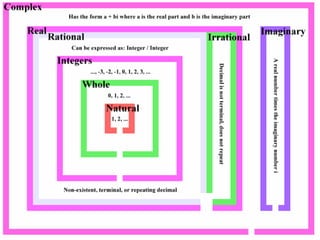
The document provides an overview of number systems used by different civilizations. It discusses ancient number systems including the Egyptian use of base-12 and Babylonian use of base-60. The decimal system is introduced as the most common modern system using base-10. Other number systems mentioned include binary, Mayan vigesimal, and fractions in ancient Egypt. Real numbers are defined as including integers, rational numbers like fractions, and irrational numbers like pi. Terminating, non-terminating recurring, and non-terminating non-recurring decimals are also briefly explained.

1. NUMBERNUMBER
SYSTEMSYSTEM
The mysterious world of numbers…
22

2. Contents
 Acknowledgment
 I ntroduction
 Brief I ntroductionabout
numbers
 History of Number System
 Number Systemaccordingto
different civilizations
 Typesof Numbers
 Decimal ExpansionOf
Number System
 Scientistsrelated toNumber
System
 What isanumber line?
 What isthedifference
betweennumeral and number?
 Word Alternatives

3. ACKNOWLEDGEMENT
We would like to thank Teema madam for giving us an
opportunity to express ourselves via mathematical
projects. We are also thankful to Bharti madam, our
computer teacher for letting us use the school computers
for presentation and providing us with an e­mail ID.
Also, we thank our friends for their ideas and co­
operation they provided to us. We are grateful to all of
them.

4. IntroductionIntroduction
A number system defines a set of values used to
represent a quantity. We talk about the number of
people attending school, number of modules taken
per student etc.
Quantifying items and values in relation to each
other is helpful for us to make sense of our
environment.
The study of numbers is not only related to
computers. We apply numbers everyday, and
knowing how numbers work, will give us an
insight of how computers manipulate and store
numbers.

5. A number is a mathematical object used in
counting and measuring. It is used in counting
and measuring. Numerals are often used for
labels, for ordering serial numbers, and for codes
like ISBNs. In mathematics, the definition of
number has been extended over the years to
include such numbers as zero, negative numbers,
rational numbers, irrational numbers, and
complex numbers.

6. Numbers were probably first used many thousands
of years ago in commerce, and initially only whole
numbers and perhaps rational numbers were
needed. But already in Babylonian times, practical
problems of geometry began to require square
roots.
Certain procedures which take one or more
numbers as input and produce a number as output
are called numerical operation.

7. TheHistoryOf NumberSystem
The number system with which we are
most familiar is the decimal (base-10)
system , but over time our ancestor have
experimented with a wide range of
alternatives, including duo-decimal
(base-12), vigesimal (base-20), and
sexagesimal (base-60)…

8. TheAncientEgyptians
TheAncient Egyptians experimented withduo-decimal
(base-12) systeminwhichtheycountedfinger-jointsinsteadof
finger.Eachof ourfingerhasthreejoints.Inaddition totheir
base-twelvesystem,theEgyptiansalsoexperimentedwitha
sort–of-base-tensystem.Inthissystem,thenumber1 through
9weredrawnusingtheappropriatenumber of vertical lines.
A human hand palm was the way
of counting used by the
Egyptians…

9. TheAncientBabylonians
Babylonians, were famous for their astrological observations
and calculations, and used a sexagesimal (base-60) numbering
system. In addition to using base sixty, the babylonians also
made use of six and ten as sub-bases. The babylonians
sexagesimal system which first appeared around 1900 to 1800
BC, is also credited with being the first known place-value of a
particular digit depends on both the digit itself and its position
within the number . This as an extremely important
development, because – prior to place-value system – people
were obliged to use different symbol to represent different
power of a base.

10. Aztecs,Eskimos,AndIndian
Merchants.
Other cultures such as the Aztecs, developed vigesimal
(base-20) systems because they counted using both finger and
toes. The Ainu of Japan and the Eskimos of Greenland are two
of the peoples who make use of vigesimal systems of present
day . Another system that is relatively easy to understand is
quinary (base-5), which uses five digit : 0, 1, 2, 3, and 4. The
system is particularly interesting , in that a quinary finger-
counting scheme is still in use today by Indian merchant near
Bombay . This allow them to perform calculations on one hand
while serving their customers with the other.
Aztecs were the ethnic
group of Mexico

11. NumberSystemaccordingtoNumberSystemaccordingto
differentcivilizations…differentcivilizations…

12. THEDECIMAL NUMBER
SYSTEM
The number system we use on day­to­day basis
in the decimal system , which is based on ten
digits: zero through nine. As the decimal system
is based on ten digits, it is said to be base ­10 or
radix­10. Outside of specialized requirement
such as computing , base­10 numbering system
have been adopted almost universally. The
decimal system with which we are fated is a
place­value system, which means that the value
of a particular digit depends both on the itself
and on its position within the number.

13. MAYAN NUMBER SYSTEM
This system is unique to our current decimal
system, as our current decimal system uses base
­10 whereas, the Mayan Number System uses
base­ 20.
The Mayan system used a combination of two
symbols. A dot (.) was used to represent the units
and a dash (­) was used to represent five. The
Mayan's wrote their numbers vertically as
opposed to horizontally with the lowest
denomination on the bottom.
Several numbers according to Mayan
Number System

14. BINARY NUMBER
SYSTEM
Thebinary numeral system,or -2base number system,
representsnumericvaluesusingtwosymbols,0and1.More
specifically,theusual base-2systemisapositional notationwith
aradixof 2. Owingtoitsstraightforwardimplementationin
digital electroniccircuitryusinglogicgates,thebinarysystemis
usedinternallybyall moderncomputers.Countinginbinaryis
similartocountinginanyothernumbersystem.Beginningwith
asingledigit,countingproceedsthrougheachsymbol,in
increasingorder.Decimal countingusesthesymbols0 through
9,whilebinaryonlyusesthesymbols0 and1.

15. FRACTIONSANDANCIENT
EGYPT
AncientEgyptianshadanunderstandingof fractions,
howevertheydidnotwritesimplefractionsas3/5or4/9
becauseof restrictionsinnotation.TheEgyptianscribe
wrotefractionswiththenumeratorof 1.Theyusedthe
hieroglyph “anopenmouth" abovethenumbertoindicate
itsreciprocal.Thenumber5,written,asafraction1/5
wouldbewrittenas.. .Therearesomeexceptions.There
wasaspecial hieroglyphfor2/3,,andsomeevidencethat
3/4alsohadaspecial hieroglyph.All otherfractionswere
writtenasthesumof unitfractions.Forexample3/8was
writtenas1/4+ 1/8.

18. Thereal numbersincludeall of themeasuring
numbers.Real numbersareusuallywrittenusing
decimal numerals,inwhichadecimal pointisplaced
totherightof thedigitwithplacevalueone.
 Itincludesall typesof numberssuchasIntegers,
Wholenumbers,Natural numbers,Rational number,
Irrational numbersandetc… Letusseethemin
detail…

19. A rational numberisanumberthat
canbeexpressedasafractionwith
anintegernumeratorandanon-zero
natural numberdenominator.The
symbol of therational numberis
‘Q’.Itincludesall typesof numbers
otherthanirrational numbers,i.e.it
includesintegers,wholenumber,
natural numbersetc…

20. This is a type of a rational number. Fractions are
written as two numbers, the numerator and the
denominator ,with a dividing bar between them.
 In the fraction m/n ‘m’ represents equal parts,
where ‘n’ equal parts of that size make up one
whole.
 If the absolute value of m is greater than n ,then
the absolute value of the fraction is greater than
1.Fractions can be greater than ,less than ,or equal
to1 and can also be positive ,negative , or zero.

21. If a real number cannot be written as a fraction of
two integers, i.e. it is not rational, it is called
irrational numbers . A decimal that can be written
as a fraction either ends(terminates)or forever
repeats about which we will see in detail further.
Real number pi (π) is an example of irrational.
π=3.14159365358979……the number neither
start repeating themselves or come in a specific
pattern.

22.  Integers are the number which includes
positive and negative numbers.
 Negative numbers are numbers that are less
than zero. They are opposite of positive
numbers . Negative numbers are usually
written with a negative sign(also called a
minus sign)in front of the number they are
opposite of .When the set of negative
numbers is combined with the natural
numbers zero, the result is the set of integer

23.  The most familiar numbers are the natural
numbers or counting numbers: One, Two,
Three and so on….
 Traditionally, the sequence of natural
numbers started with 1.However in the 19th
century, mathematicians started including 0
in the set of natural numbers.
 The mathematical symbol for the set of all
natural numbers is ‘N’.

24. Moving to a greater level of abstraction, the real numbers can
be extended to the complex numbers. This set of number
arose historically, from trying to find closed formulas for the
roots of cubic and quadratic polynomials. This led to
expressions involving the square roots of negative numbers,
eventually to the definition of a new number: the square root
of negative one denoted by “I”. The complex numbers consist
of all numbers of the form (a+bi) ; Where a and b are real
numbers.

25. OtherTypes
There are different kind of other numbers too. It includes
 hyper-real numbers,
 hyper-complex numbers,
 p-adic numbers,
 surreal numbers etc.
These numbers are rarely used in our day-to-day life. Therefore,
we need not know about them in detail.

26. Decimal Expansionof Numbers
A decimal expansion of a number can be either,
 Terminating
 Non­terminating, non recurring
 Non terminating, recurring
Let us see each of the following
briefly…

27. Terminatingdecimal
A decimal expansion in which the remainder becomes
zero. For example, 54 9 =
Terminating decimal is always a rational number. It can
be written in p/q form.
549
6
54
0
As the remainder is zero, this
is a terminating decimal

28. Nonterminatingnon
recurring
“Recurring” means “repeating”. In this form, when we
divide a number by another, remainder never becomes
zero, and also the number does not repeat themselves in
any specific pattern. If a number is non terminating and
non repeating, they are always classified as irrational
number. For example,
0.10100100010000100000100.... does have a pattern,
but it is not a fixed-length recurring pattern, so the
number is irrational.

29. Nonterminating,recurring
In this form, when a number is divided by the
other, the remainder never becomes zero,
instead the numbers of the quotient start
repeating themselves. Such numbers are
classified as rational numbers. For example,
3.7250725072507250…
In this example, “ 7250” have started repeating
itself. Hence, it is a rational number. It can be
expressed in p/q form.

30. MathematiciansrelatedtoNumber
System
Euclid :
Euclid was an ancient mathematician from
Alexandria, who is best known for his major work,
Elements. He told about the division lemma,
according to which,
A prime number that divides a product of two
integers must divide one of the two integer.
Euclid – The father of geometry

31. MathematiciansrelatedtoNumber
System
R. Dedekind And G. Cantor :
In 1870s two German mathematicians; Cantor and
Dedekind, showed that :
Corresponding to every real number, there is a point
on the number line, and corresponding to every point
on the number line, there exists a unique real
number.
R. DedekindG. Cantor

32. Archimedes :
He was a Greek mathematician. He was the first to
compute the digits in the decimal expansion of π (pi). He
showed that -
3.140845 < π < 3.142857
MathematiciansrelatedtoNumber
System
Archimedes

33. A number line is a line with marks on it that are placed
at equal distance apart. One mark on the number line is
usually labeled zero and then each successive mark to
the left or to the write of the zero represents a
particular unit such as 1, or 0.5. It is a picture of a
straight line.
A number line

34. No, number and numerals are not same.
Numerals are used to make numbers. It is a
symbol used to represent a number.
For example, the NUMERAL 4 is the name of
NUMBER four.
Numeral “7”
Number 7

35. WordAlternativesWordAlternatives
Some numbers traditionally have words to express them,
including the following:
 Pair, couple, brace: 2
 Dozen: 12
 Bakers dozen: 13
 Score: 20
 Gross: 144
 Ream(new measure): 500
 Great gross: 1728

37. Project made and Compiled by ~
Samarth Agrawal
Yogesh Surve
Arnab Das
Arijit Sharma
Ankita Sinha
Ayushi Sur
Nimisha Singh