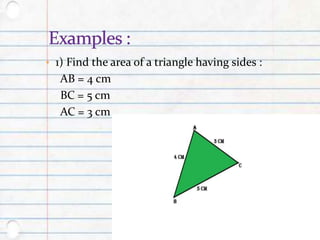
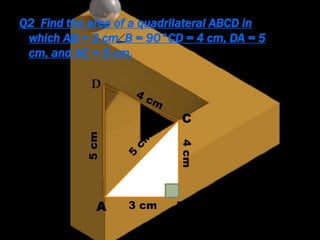
Heron's Formula provides a method for calculating the area of a triangle when the lengths of all three sides are known, allowing for applications in real-life scenarios such as land measurement. Hero of Alexandria, a Greek mathematician and inventor, contributed significantly to mathematics and mechanics around the first century AD, though little is known about his life. His notable works include 'Metrica', which discusses area and volume calculations, and various texts on mechanics and optics.

3. Heron’s Formula
About Heron Needs of
Heron’s
Formula
Area of
Triangles
and some
other shapes
Questions

4.  Born / Died When Heron lived is not well established. Most
accounts place his life around 0 AD.
 Heron, (also known as Hero) was a Greek mathematician.
Some authorities place his birthday early 150 BCE in
Ptolemaic, Egypt. While other scholars have dated his birth to
be 250 CE in late Roman Empire. Nothing is really known of
Hero's life, but what we do know comes from clues in the 14
known books by him.

5.  As a student, Hero spent most of his time in the
Library at the University of Alexandria. He loved to be
in the library, because of the series of gardens vast
collection of books. Hero was strongly influenced by
the writings of Ctesibius of Alexandria. He may have
been a student of Ctesibius. When older he taught at
the University of Alexandria, and taught mathematics,
mechanics, and physical science. He wrote many
books and he used them as texts for his students, and
manuals for technicians, and were written in Greek,
Latin and Egyptian.

6.  Some of Heron's books
 Baroulkos
 Berlopoeica (in Greek and Roman Artillery, Technical Treatises, 1971)
 Catoptrica (in Latin)
 Chieroballistra (in Greek and Roman Artillery; Technical Treatises, 1971)
 Dioptra (partical English translation, 1963)
 Eutocuis
 Geometrica
 Mechanica (3 volumes, in Arabic)
 Metrica (3 volumes)
 Peri Automatopoitikes (Automata, 1971)
 Peri Metron (also called Mensurae)
 Pneumatica (2 volumes: The Pneumatica of Hero Of Alexandria, 1851)
 Stereometrica

7.  One of his books, Metrica, was lost until the end of the
19th century. Scholars knew of its existence only
through one of his other books, Eutocuis. In 1894,
historian Paul Tannery discovered a fragment of the
book in Paris. Then, in 1896, R. Schone found a
complete copy in Constantinople. This book is the
most famous book that Hero wrote. It consists of 3
volumes, and shows ways to calculate area and volume,
and their divisions.

8.  He was an accomplished inventor and mechanical
engineer. Among his inventions were a reaction steam
turbine, a vending machine, and a wind-powered
organ.

9.  i)area=1/2 (b x h)
 Let there be a scalene triangle, the lengths of its
sides are known but the height is not known. To
find its area none of above listed formulae is
applicable. In fact, we require the height
corresponding to a base. But we do not have any
clue for the same. Heron , an encyclopedic writer in
Applied Mathematics gave a formula for finding
area of triangle in terms of lengths of its three sides
as discussed in next slide.

10. o We can calculate the area of a triangle if we know the
lengths of all three sides, using a formula that has
been known for nearly 2000 years.
o It is called "Heron's Formula" after Hero of Alexandria
o The formula can be written as :
o S=

11.  Herons formula can be used to measure the area of a
triangle whose sides are given. It helps you to find the
area of a triangle where the height is not given. This
includes scalene, isosceles and equilateral triangles
 It can be used in our daily life in the following ways.-
 (i) When we buy a piece of land we can find its area by
using herons formula
 (ii) Imagine someone gave you a triangular figure(it
can be 2d or 3d) now u can find its area by just
applying herons formula.

12.  Example : If a farmer wishes to find the area of his
field which is in shape of quadrilateral. He needs to
divide the quadrilateral in triangular parts and he uses
the Heron’s formula for the area of a triangular part.

19.  RECTANGLE If l and b denote respectively the length
and breadth of a rectangle, then
(i) Perimeter = 2(l + b)
(ii) Area = l x b

20.  If a denote the length of each side of a square , then
 (i) Perimeter = 4a
 (ii) Area = a² = (side)²
 (iii) Area = ½ (Diagonal)²

21.  (i) Perimeter = 2(AB + BC) = 2(l + b )
 (ii) Area = Base x Height

22.  If d1 and d2 are the lengths of the diagonals of a
rhombus of side a, then
 (i) Perimeter = 4a = 4(side)
(ii) Area = ½ (d1 x d2)

23. • 1) Find the area of a triangle having sides :
AB = 4 cm
BC = 5 cm
AC = 3 cm

24.  Given Sides : AB = a = 4 cm
 AC = b = 3 cm
 BC = c = 5 cm

27. Q2 Find the area of a quadrilateral ABCD in
which AB = 3 cm, B = 90°CD = 4 cm, DA = 5
cm, and AC = 5 cm.
5cm
4cm
3 cm
D
A B
C

28. Area of ∆ ABC = ½ × AB × BC
= ( ½ × 3 × 4) cm²
= 6 cm²
For Δ ACD:
Let a = 5 cm, b = 4 cm and c = 5 cm.
then,
s = ½ × (a + b + c)
s = ½ ( 5 + 4 + 5 ) cm
s = ½ × 14 cm
s = 7 cm

29. Now, s – a = ( 7 – 5 ) = 2 cm
s – b = ( 7 – 4 ) = 3 cm
s – c = ( 7 – 5 ) = 2 cm
Area of ∆ ACD = √s(s — a)(s —b)(s—c)
= √ 7 (2) (3) (2)
= √ 2 × 2 × 3 × 7
= 2 × √3 ×√7
= 2 × √21
= 2 × 4.58 = 9.167 /
-
Area of quadrilateral ABCD = Area of ∆ABC +
Area of ∆ ACD
= 6 + (9.16) cm²
= 15.2 cm² (approx.)