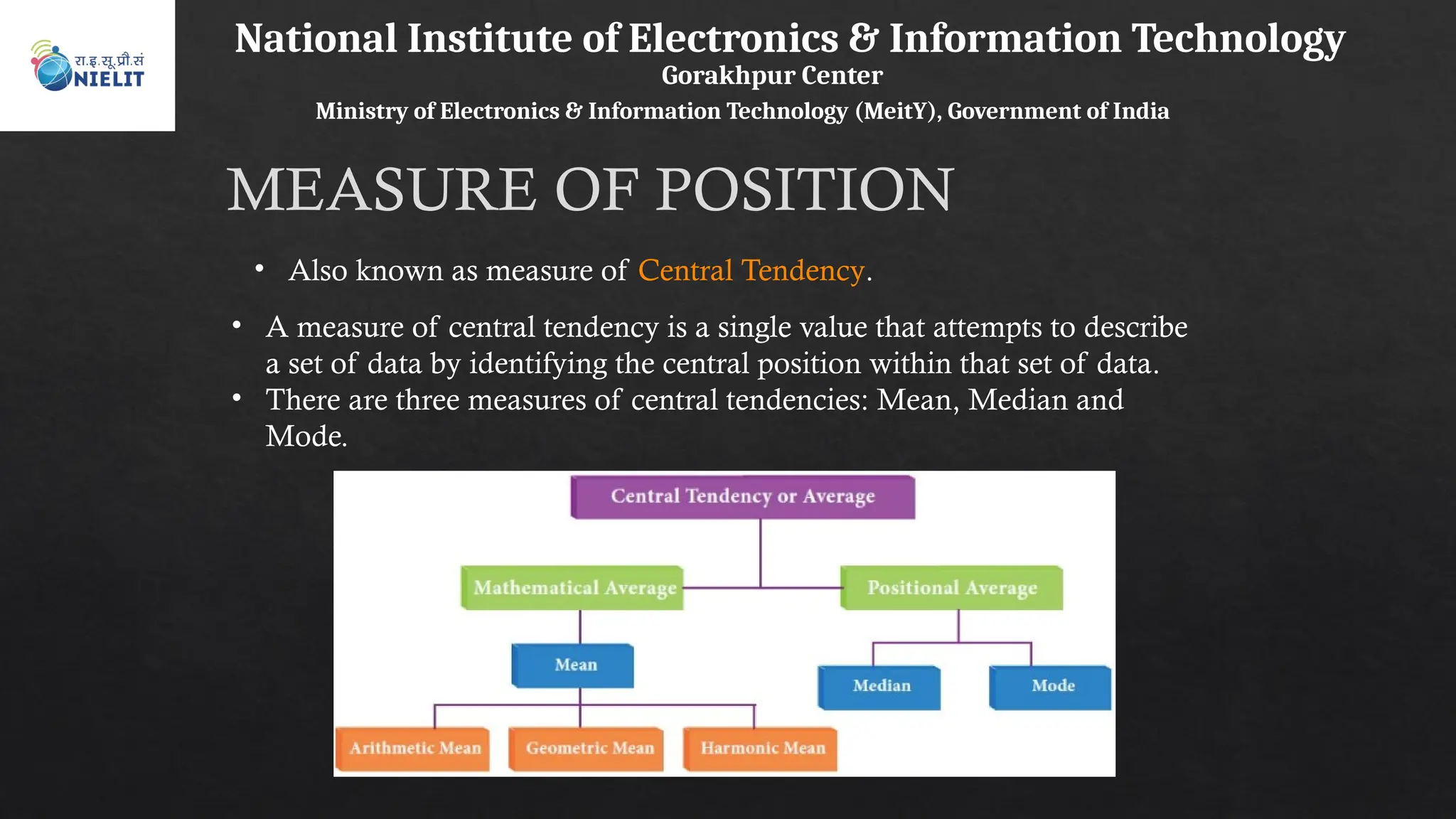
The document provides a comprehensive introduction to matrices, highlighting their definition, properties, and operations such as addition, subtraction, multiplication, and inversion. It emphasizes key concepts like determinants, minors, and cofactors, as well as various matrix types including symmetric and nonsingular matrices. Additionally, it outlines essential matrix operations and laws that govern matrix multiplication and transposition.



![Matrices - Introduction
A matrix is denoted by a bold capital letter and the elements within the
matrix are denoted by lower case letters
e.g. matrix [A] with elements aij
mn
ij
m
m
n
ij
in
ij
a
a
a
a
a
a
a
a
a
a
a
a
2
1
2
22
21
12
11
...
...
i goes from 1 to m
j goes from 1 to n
Amxn= mAn
=
National Institute of Electronics & Information Technology
Ministry of Electronics & Information Technology (MeitY), Government of India
Gorakhpur Center](https://image.slidesharecdn.com/day1-2-241001041427-796f83a8/75/mathematics-for-machine-learning-matrices-pptx-4-2048.jpg)














![Matrices - Operations
If A = [A] is a single element (1x1), then the determinant is
defined as the value of the element
Then |A| =det A = a11
If A is (n x n), its determinant may be defined in terms of
order (n-1) or less.
National Institute of Electronics & Information Technology
Ministry of Electronics & Information Technology (MeitY), Government of India
Gorakhpur Center](https://image.slidesharecdn.com/day1-2-241001041427-796f83a8/75/mathematics-for-machine-learning-matrices-pptx-19-2048.jpg)