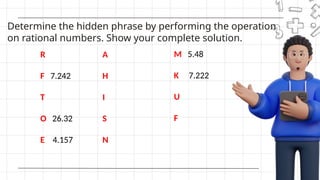
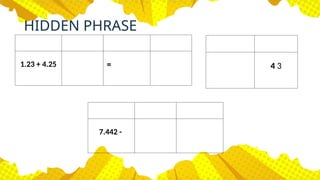
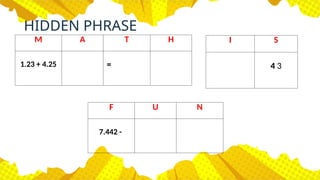
The document outlines a lesson plan focused on operations with rational numbers, including addition, subtraction, multiplication, and division of fractions and decimals. It includes objectives, examples, and step-by-step methods for performing these operations, along with activities to reinforce learning. Key vocabulary defines terms such as fractions, proper/improper fractions, and decimals, while seeking to engage students with applicable real-world scenarios and assessments.

1. OPERATIONS
ON RATIONAL
NUMBER
RAT IONAL NUMBE RS
QUART ER 1 | LESS ON 5

2. • Perform Operations on Rational Numbers;
• Solve problems involving operations on
rational numbers;
LESSON
OBJECTIVES

3. DAY
1

4. DAY 1
RECAP
• What are rational numbers?
• What are similar fractions?
• What are dissimilar fractions?
• How do we add or subtract similar fractions?
• How do we add or subtract dissimilar fractions?
• How do we multiply fractions?
• How do we divide fractions?

5. DAY 1
RECAP
• Can you describe a situation where you
might need to use fractions in cooking or
baking? How do fractions help in that
situation?

6. DAY 1 RECAP

7. Instructions: Perform the following
operations on fractions and decimals.
Express your answer in lowest term.

8. 1.) +
2.) -
3.) .
4.) +
5.) /
6.) +
7.)
8.)
9.)
10.)

9. 1.)
2.)
3.)
4.)
5.) 8
6.) 1
7.)
8.)
9.)
10.)
Answer Key:

10. Have you ever
wondered how we
calculate discounts,
taxes or
measurements

11. If you and three of your classmates are going to
eat pizza in the fast-food chain, how will you
divide this pizza?
PIZZA FRACTION.

12. Content Area Vocabulary
Fractions
- are a type of number that are used to
represent parts of a whole.

13. Content Area Vocabulary
Proper Fraction
In proper fraction, the numerator is smaller
than the denominator.
Example:

14. Content Area Vocabulary
Improper Fraction
In improper fraction, the numerator is
larger than denominator.
Example:

15. Content Area Vocabulary
Decimal
- is a fraction written in a special form.
- it comes from the Latin word decimus,
meaning tenth, from tye root word dedem,
or 10.

16. Day
2

17. Observe the following examples
below:
1. + =
2. +(-) = + (-)= -
3. . =
4. -) = - . = - = -8

18. What have you observed in
adding fractions with the
same denominator? with
different denominators?

19. What have you observed in
multiplying fractions? Is it
the same as multiplying
integers?

20. What have you observed in
dividing fractions? What
happened to the
denominator?

21. How about this expression,
(4.6 . 3.2) – 0.89 +

22. How are we going to solve
this? What is the result of this
expression?

23. The given problems are
example of performing
operations on rational
numbers.

24. Day
3

25. WORK
EXAMPLE
Perform the following operations on rational numbers.
A. Addition and Subtraction of Rational Numbers
1. 2.03 + 0.041 + 5.325 =
2. 12.245 – 4.5124 – 2.521 =
3. 4 + 3 =
4. - =
5. 6.89 - 1 =
7.396
5.2116
7
𝟐𝟖
𝟏𝟏𝟕
5.09

26. • To add or subtract two rational numbers
(fractions) with the same denominator, we
simply add and subtract the numerators and
write the result over the same denominator.
Points to consider in adding and subtracting rational
numbers
FOR FRACTIONS:

27. • When the denominators are not the same,
we must find the equivalent fractions with
the same denominators. In other words, we
make the fractions similar.
Points to consider in adding and subtracting rational
numbers
FOR FRACTIONS:

28. • For mixed numbers, convert it to improper
fractions and perform the operation.
Points to consider in adding and subtracting rational
numbers
FOR FRACTIONS:

29. Points to consider in adding and subtracting rational
numbers
FOR DECIMALS:
• Line up the decimal points vertically. Fill in any
0’s where necessary.
• Add and subtract the numbers if they were
whole numbers
• Place the decimal point in the sum or difference
so that it lines up vertically with the numbers
being added or subtracted.

30. • Convert all the terms in a similar form, either
in all decimals, or fractions.
• Follow the usual way of adding and
subtracting rational number.
Points to consider in adding and subtracting rational
numbers
FOR COMBINATION OF FRACTIONS AND DECIMALS:

31. WORK
EXAMPLE
Perform the following operations on rational numbers.
B. Multiplication of Rational Numbers
1. 3. =
2. . =
3. 4.82 . 32.4 =
4. 8 . =
1
𝟏𝟐
𝟑𝟓
138. 672
𝟏𝟓
𝟏
𝟔

32. Points to consider in multiplying rational numbers
FOR FRACTIONS:
• Rewrite any mixed number as improper
fractions.
• Multiply the numerators, and then multiply the
denominators.
• Simplify, if needed.

33. • Multiply as you would with whole numbers.
• Move the decimal point in the product one
place to the left for each decimal place in the
factors.
Points to consider in multiplying rational numbers
FOR DECIMALS:

34. • Convert all the terms in a similar form, either
in all decimals, or fractions.
• Follow the usual way of multiplying rational
number.
Points to consider in multiplying rational numbers
FOR COMBINATION OF FRACTIONS AND DECIMALS:

35. WORK
EXAMPLE
Perform the following operations on rational numbers.
C. Division of Rational Numbers
1. =
2. =
3. =
4. =
𝟐𝟖
𝟒𝟓
𝟏
𝟏𝟒
2.25
𝟑 . 𝟔𝟕

36. • Rewrite any mixed numbers as improper
fractions.
• Multiply the dividend by the reciprocal of the
divisor.
• Simplify, if needed.
Points to consider in dividing rational numbers
FOR FRACTIONS:

37. Points to consider in dividing rational numbers
FOR DECIMALS:
• Move the decimal point to the right to make the divisor a
whole number.
• Move the decimal point the same number of places to the
right in the dividend.
• Place the decimal point in the quotient directly above the
decimal point in the dividend.
• Divide until there is no remainder, or until the quotient
begins to repeat in a pattern. Annex zeros, if necessary.

38. • Convert all the terms in a similar form, either
in all decimals, or fractions.
• Follow the usual way of dividing rational
number.
Points to consider in dividing rational numbers
FOR COMBINATION OF FRACTIONS AND DECIMALS:

39. DAY
4

40. LESSON
ACTIVITY

41. Determine the hidden phrase by performing the operation
on rational numbers. Show your complete solution.
R
F 7.242
T
O 26.32
E 4.157
A
H
I
S
N
M 5.48
K 7.222
U
F

42. HIDDEN PHRASE
1.23 + 4.25 = 4 3
7.442 -

43. HIDDEN PHRASE
M A T H
1.23 + 4.25 =
I S
4 3
F U N
7.442 -

44. What new knowledge did you gain from this week’s topic?
Which part of the lesson do you find challenging to
understand?
What aspects of the lesson surprised you the most?

46. Perform the following operations on rational numbers. Show your complete solution
Round off to the nearest hundredths (for decimals). Express your answers in simples
form/mixed number (for fractions).
1.)
2.) .
3.) 4 + 1
4.) 1- +
5.) 4.24 . 3.14
6.)
7.)
8.) 4 + 6
9.)
10.)

47. Thank
You!