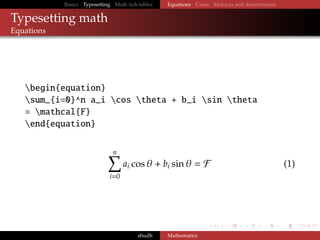
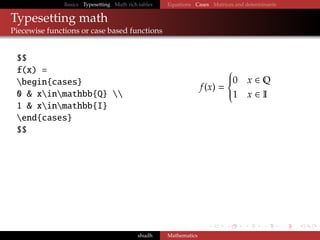
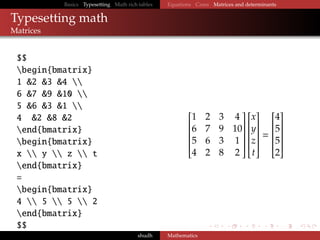
The document provides a comprehensive guide on typesetting mathematical expressions in LaTeX, covering basic commands, equation formatting, and special functions including matrices and determinants. It includes examples of inline and display math, Greek letters, and various mathematical symbols. Additionally, it details how to create rich tables that incorporate mathematical content.




![Basics Typesetting Math rich tables
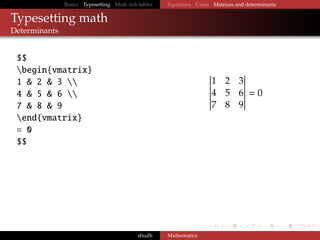
Basic commands
It is necessary to enclose all math by the $ sign.
n
$sum_{i=1}^n
a_n x^n = 0$
an xn = 0
i=1
n
$prod_{i=1}^n
a_n x^n = 1$
an xn = 1
i=1
$int x^n dx =
frac{x^{n+1}}{n+1}$
xn dx =
∞
xn dx =
$int_0^infty x^n dx =
frac{1}{n+1} left[
x^{n+1}right]_0^infty$
0
shudh
1
xn+1
n+1
4
2
${4}choose{2}$
Mathematics
xn+1
n+1
∞
0](https://image.slidesharecdn.com/mathematics-131129012134-phpapp01/85/The-LaTeX-Workshop-Typesetting-Mathematics-with-LaTeX-5-320.jpg)

![Basics Typesetting Math rich tables
Our wonderful roots
The Euclidean distance between two points $mathbf{p}
(x_1, y_1)$ and $mathbf{q}(x_2,y_2)$ is given by:
$$ d(mathbf{p}, mathbf{q}) = sqrt{(x_1-x_2)^2
+ (y_1 - y_2)^2}$$
and the Minkowski’s distance with the $p$-norm is given as
$$d_p(mathbf{p}, mathbf{q}) = sqrt[p]{vert x_1-x_2
vert ^p + vert y_1 - y_2 vert ^p}$$
produces:
The Euclidean distance between two points p(x1 , y1 ) and
q(x2 , y2 ) is given by:
d(p, q) =
(x1 − x2 )2 + (y1 − y2 )2
and the Minkowski’s distance with the p-norm is given as
dp (p, q) =
p
|x1 − x2 |p + |y1 − y2 |p
shudh
Mathematics](https://image.slidesharecdn.com/mathematics-131129012134-phpapp01/85/The-LaTeX-Workshop-Typesetting-Mathematics-with-LaTeX-7-320.jpg)