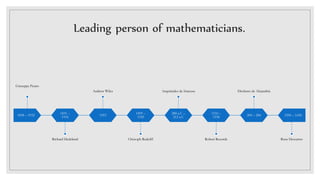
1. The document discusses various topics in mathematics including numbers, exponents, radicals, complex numbers, equations, and lines.
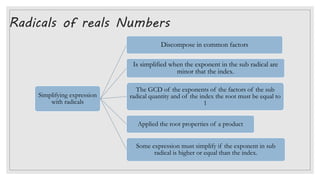
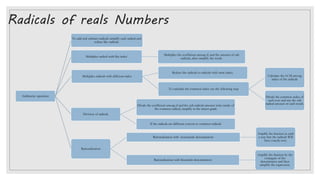
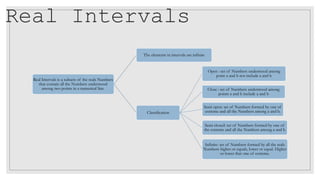
2. It defines different types of numbers such as natural numbers, integers, rational numbers, irrational numbers, and real numbers. It also discusses operations involving exponents and radicals.
3. The document also covers complex numbers, defining them as numbers that can be written in the form a + bi, where a and b are real numbers. It discusses operations and properties involving complex numbers.















































![◦ Para calcular la magnitud se utiliza la siguiente
formula:
◦ |AB| = √ [ (ABx)2 + (ABy)2]](https://image.slidesharecdn.com/1primerao-220814205535-09a4403f/85/1-primer-ano-pptx-56-320.jpg)









































