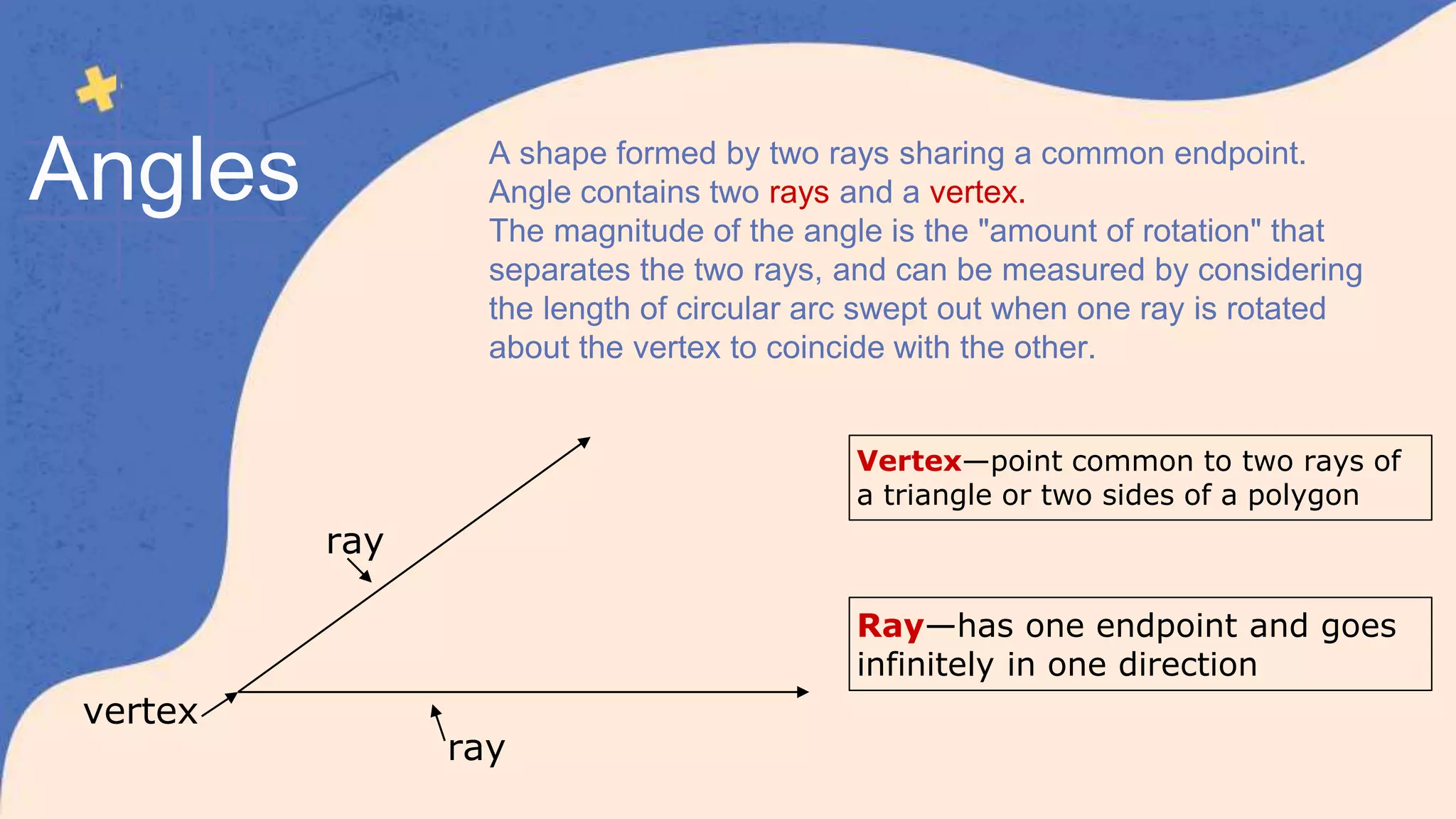
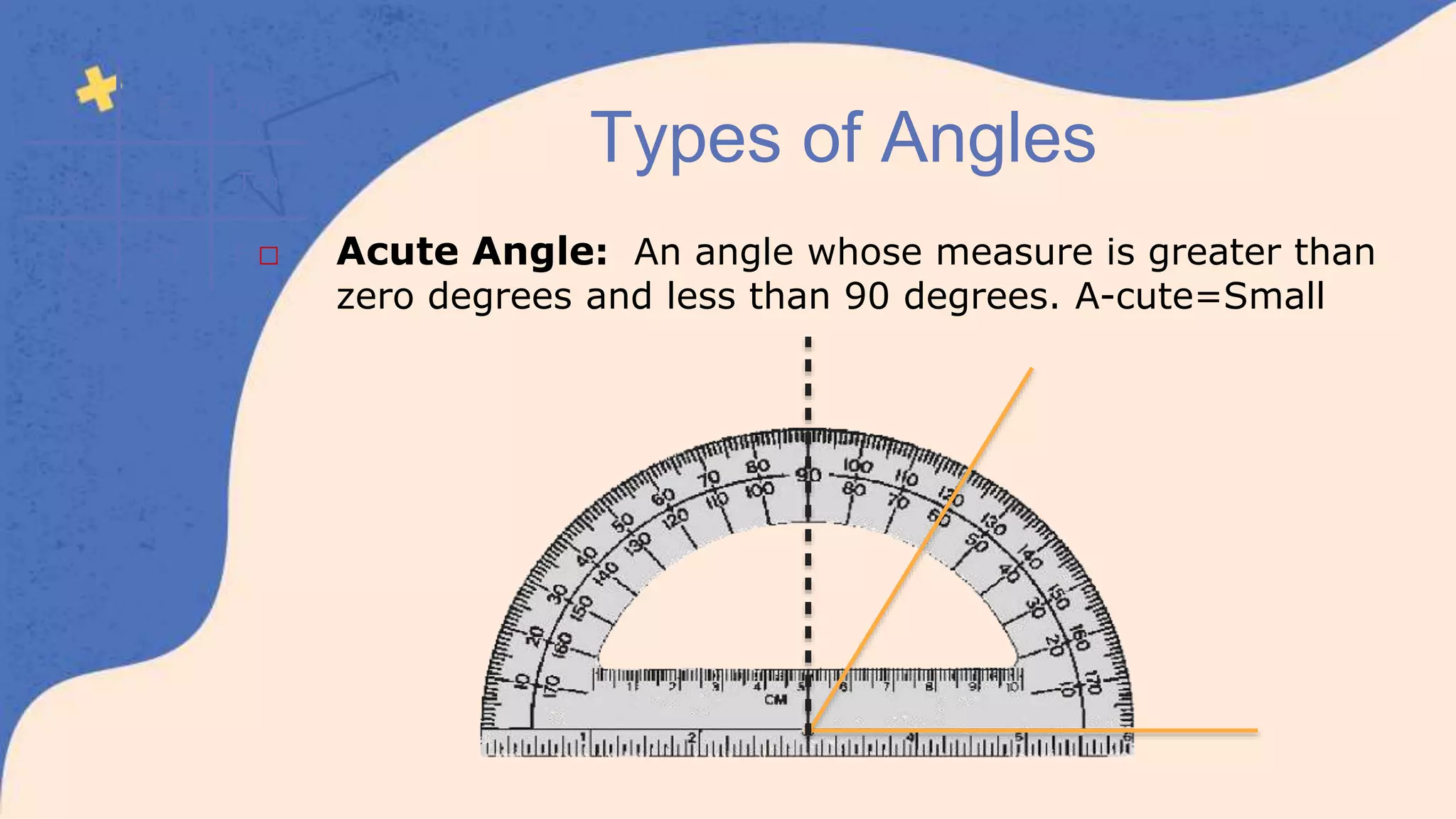
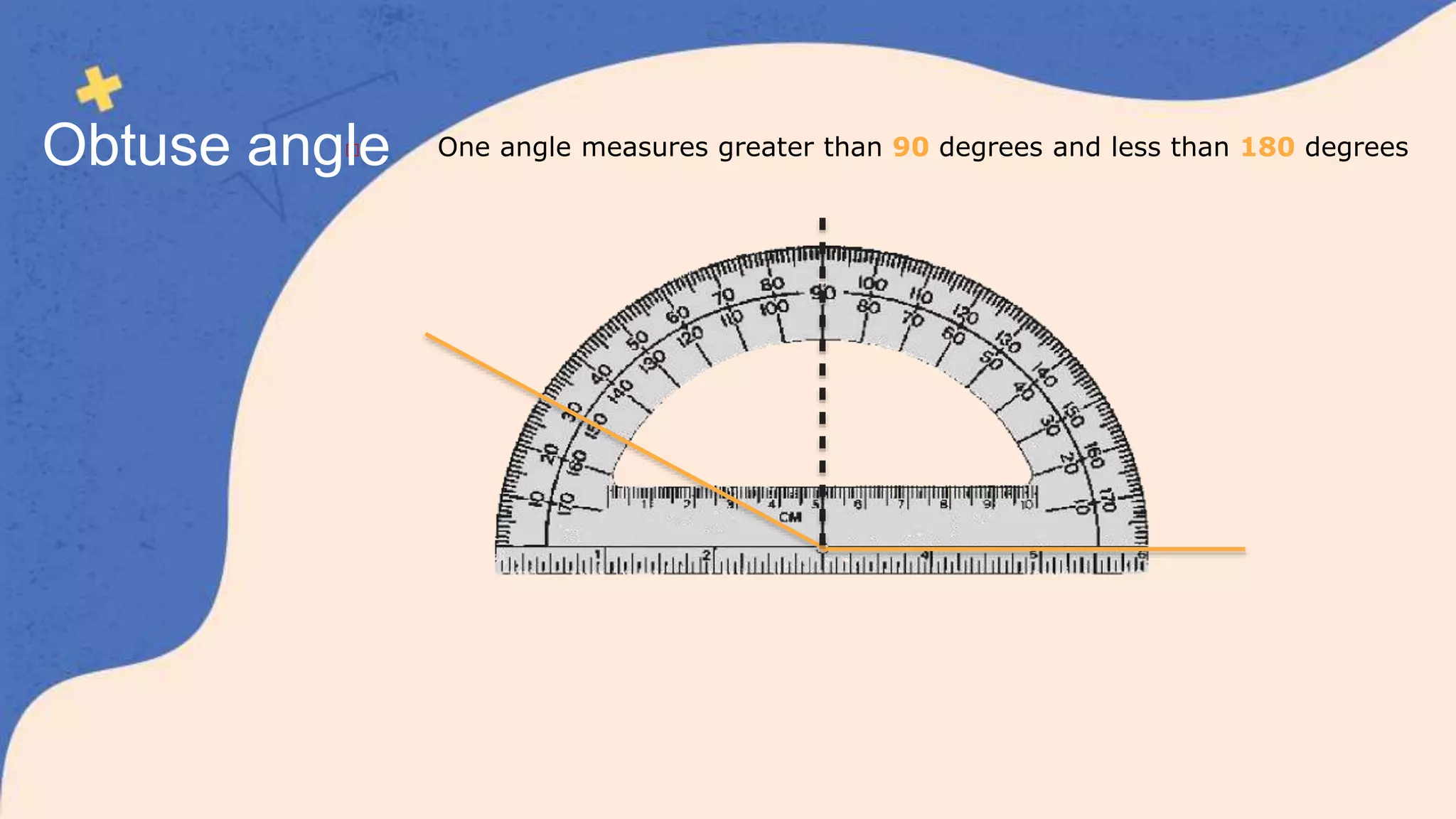
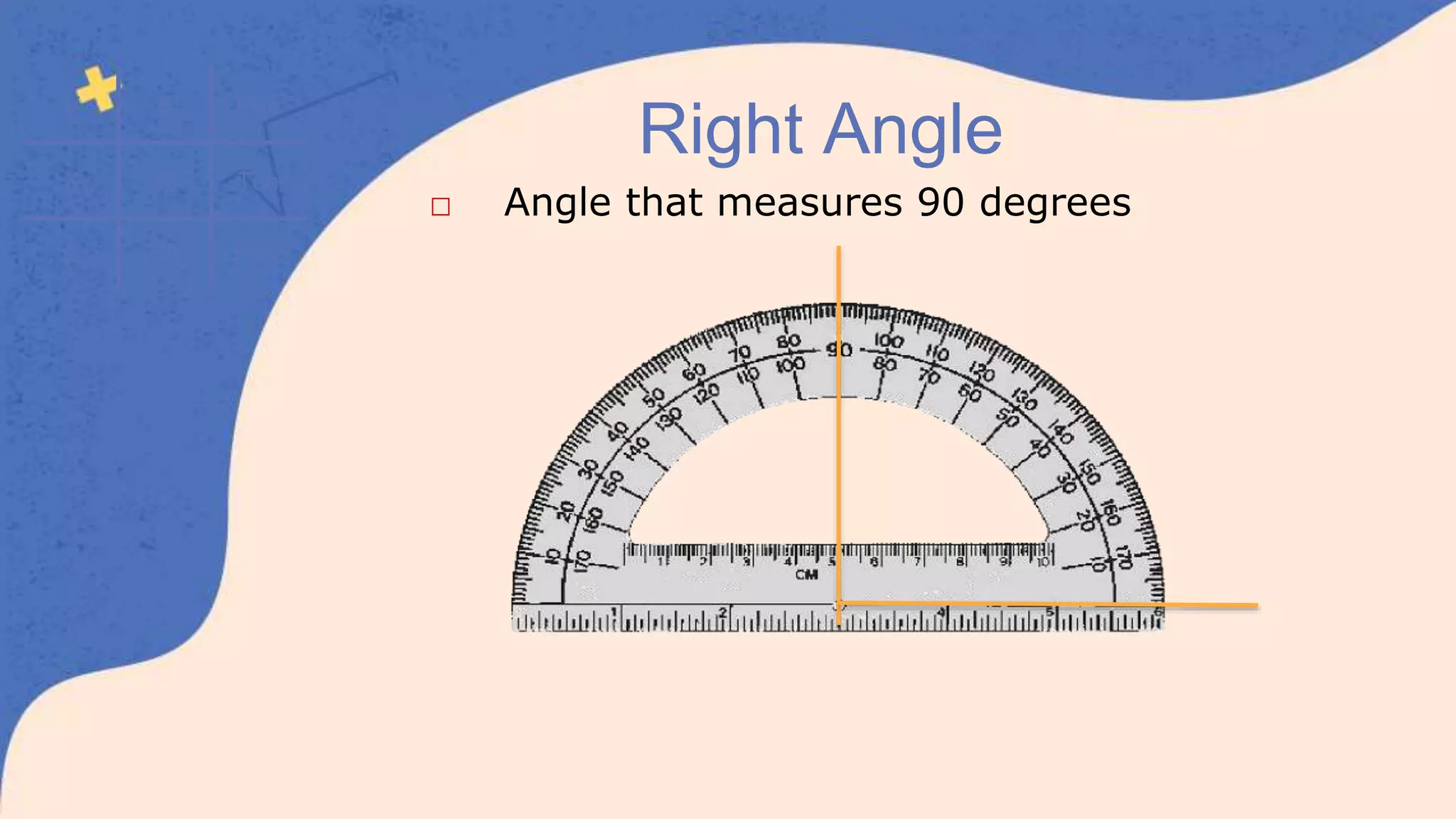
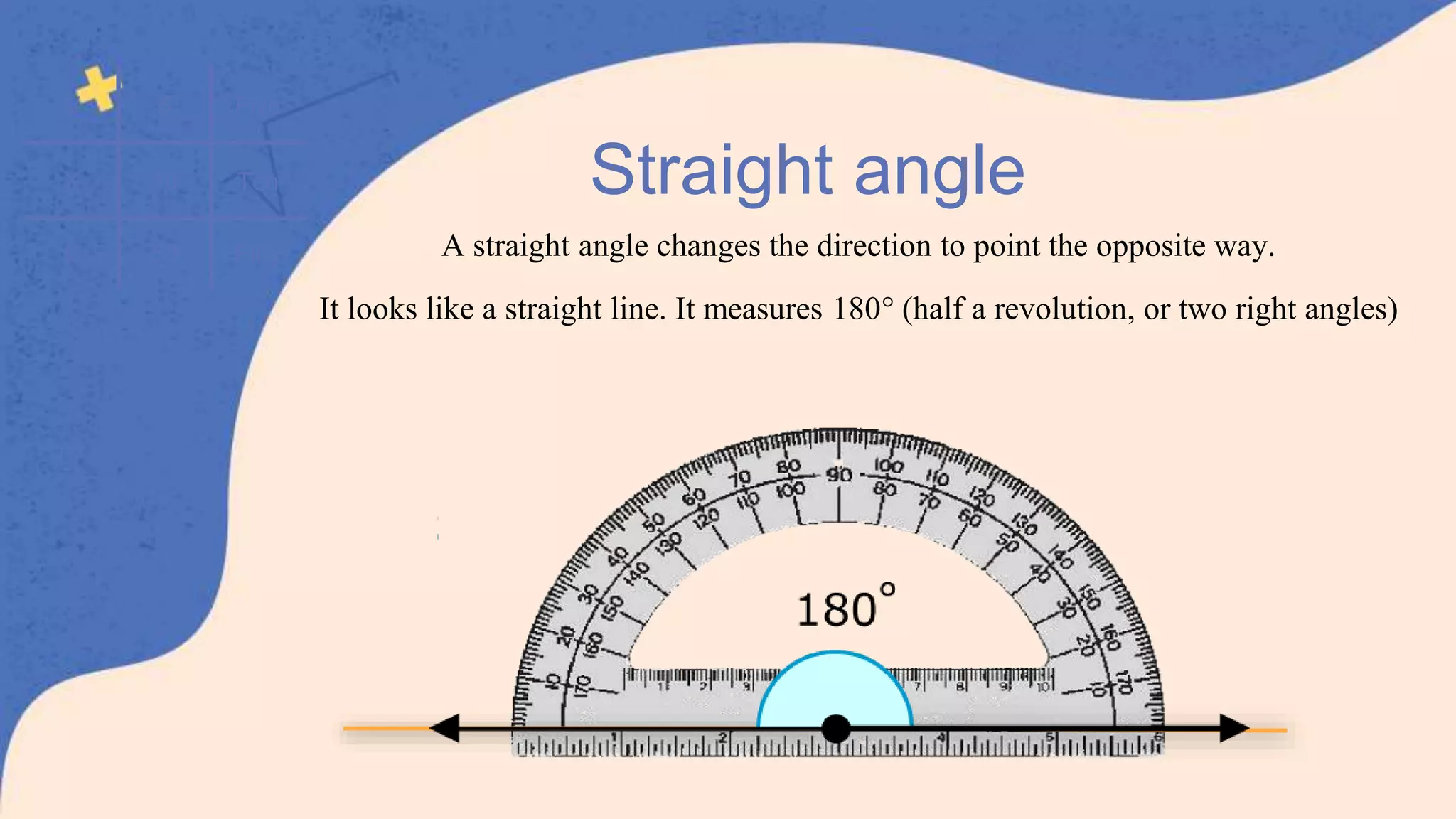
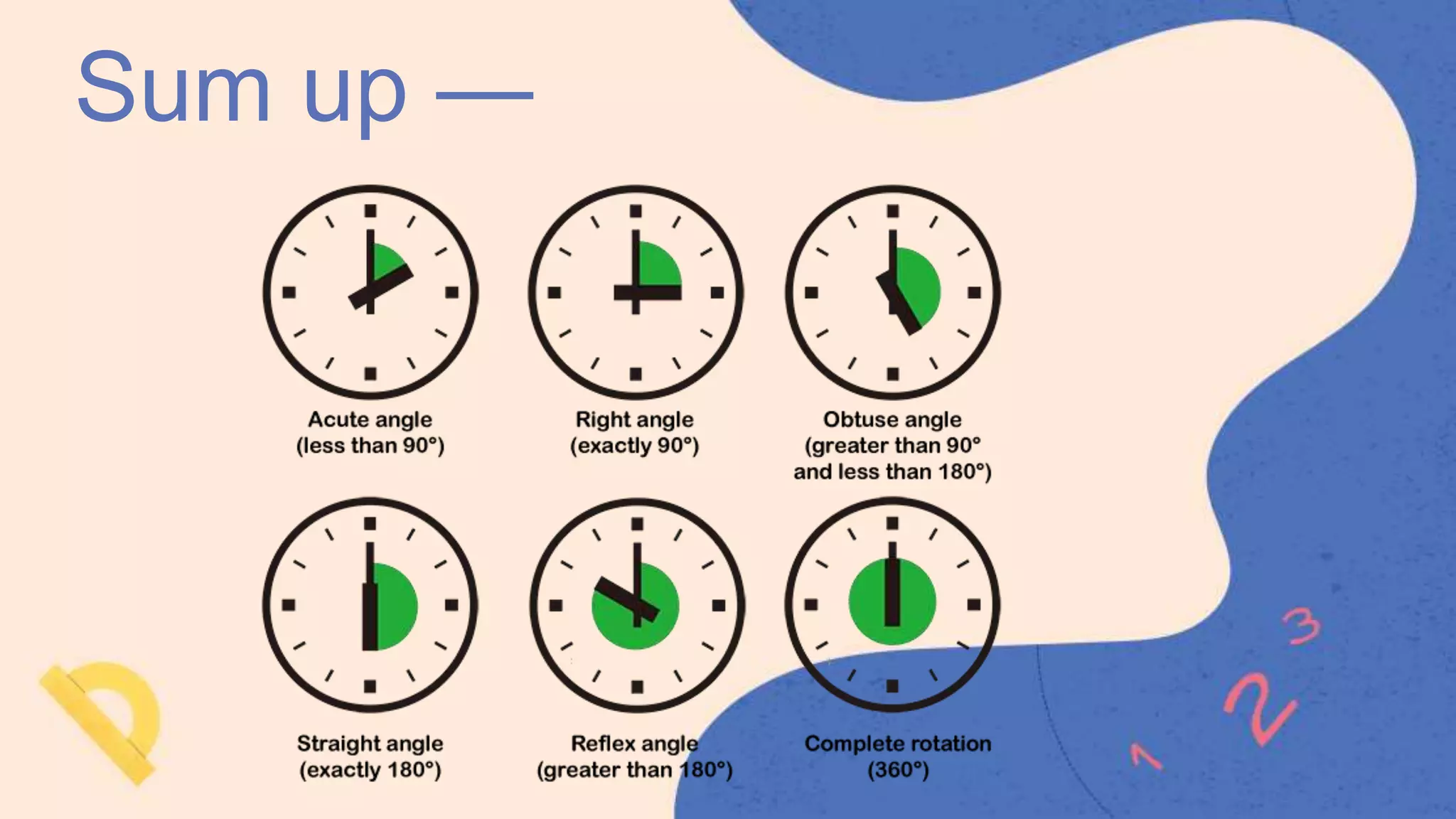
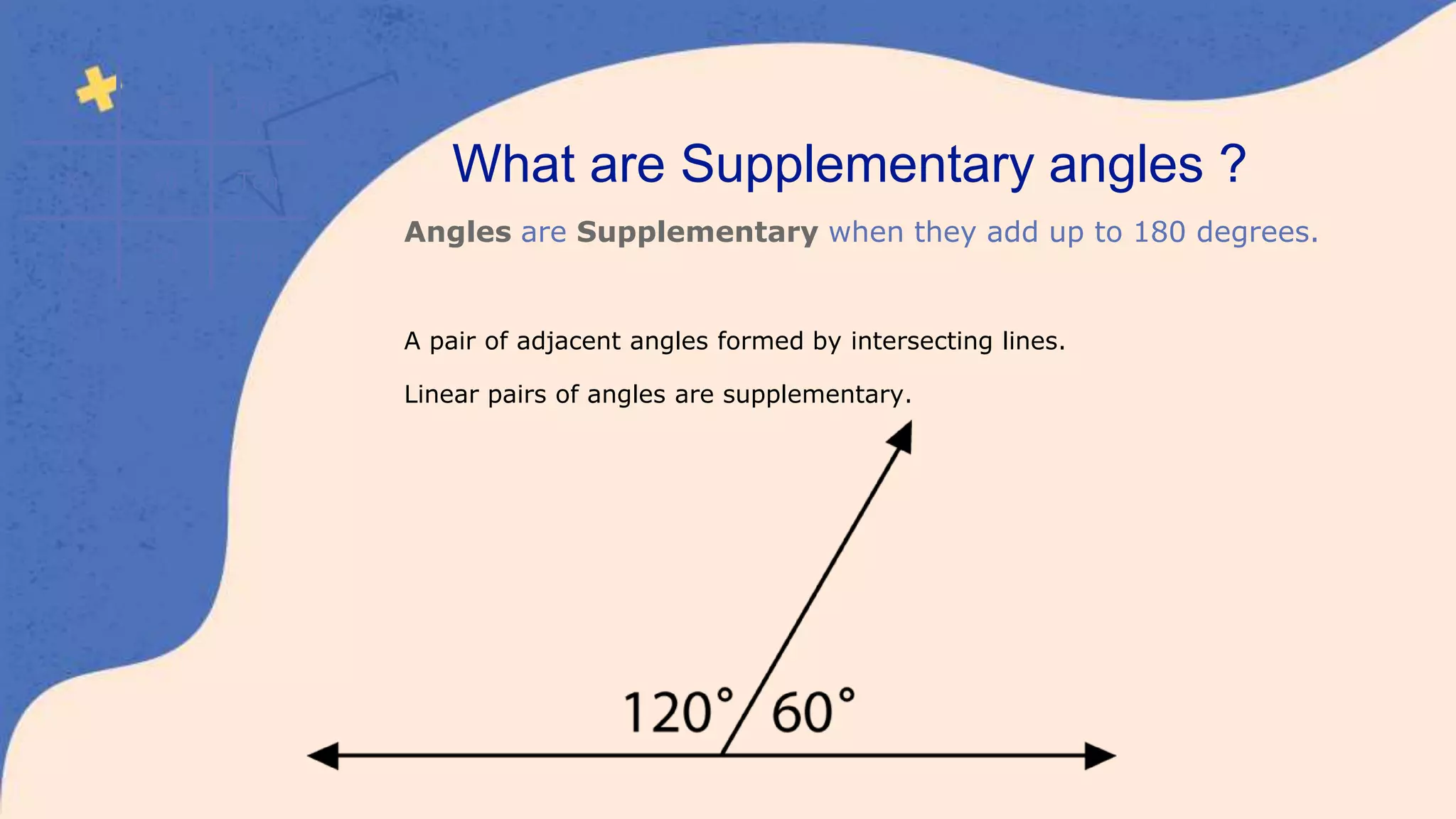
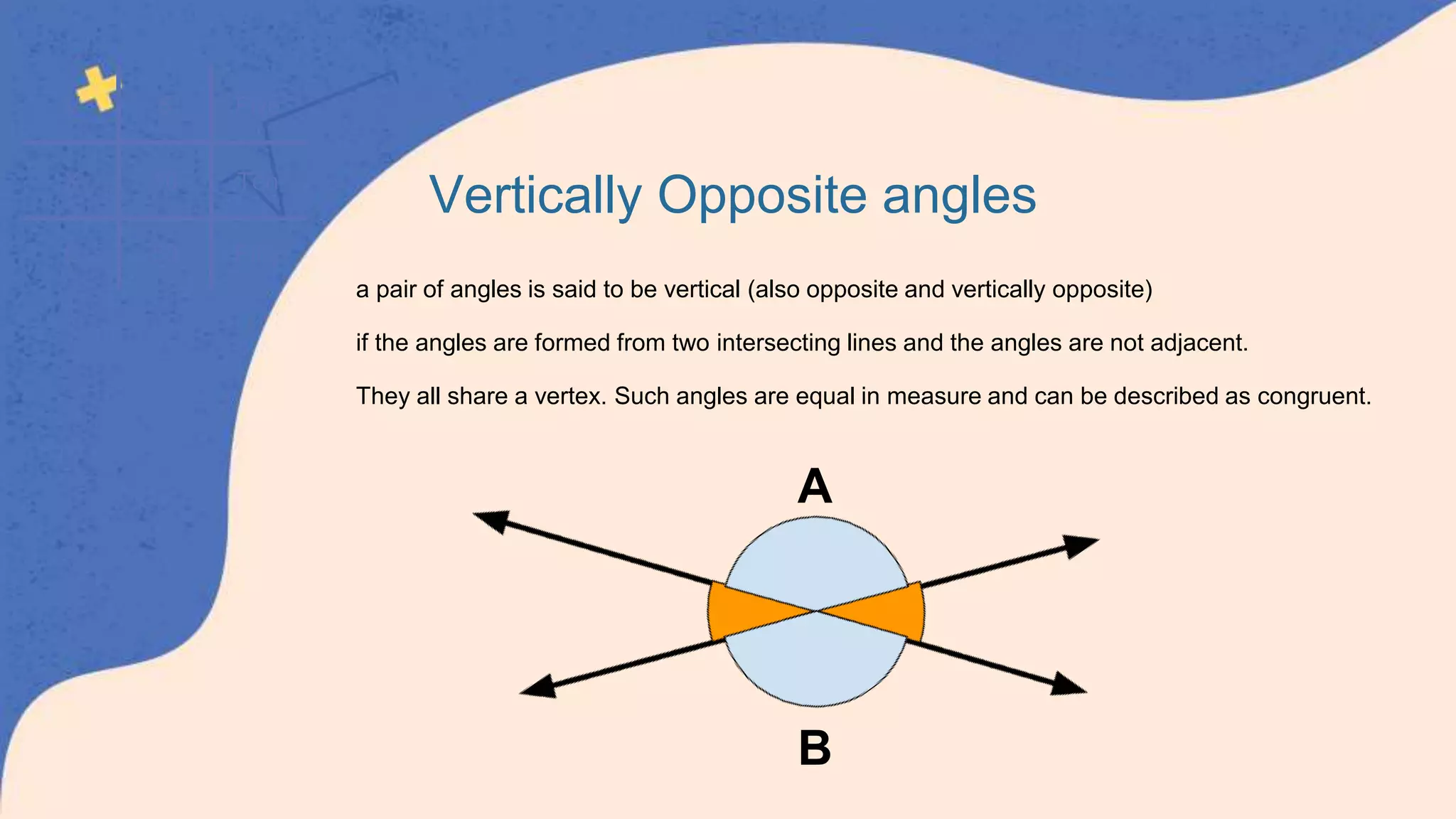
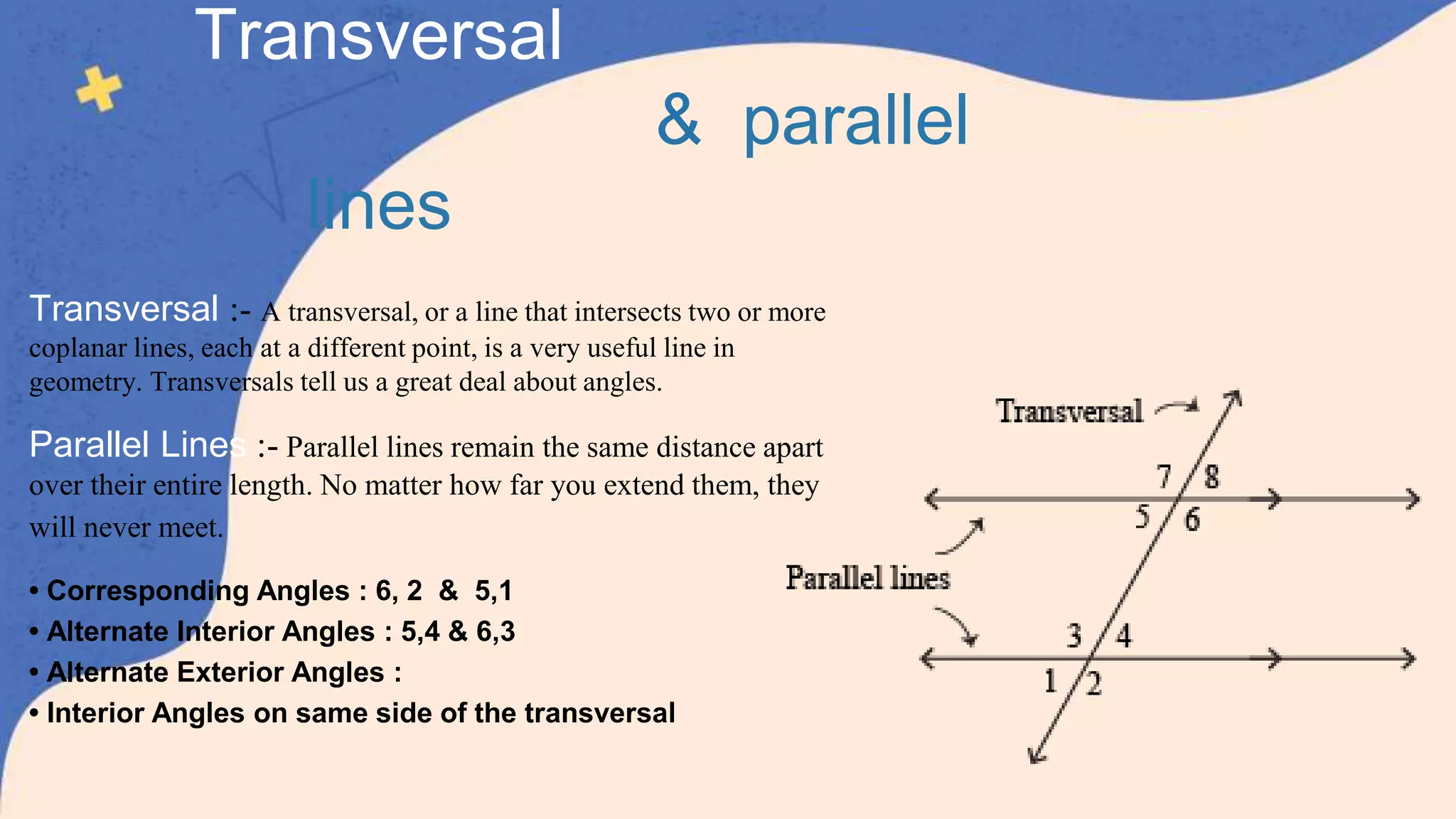
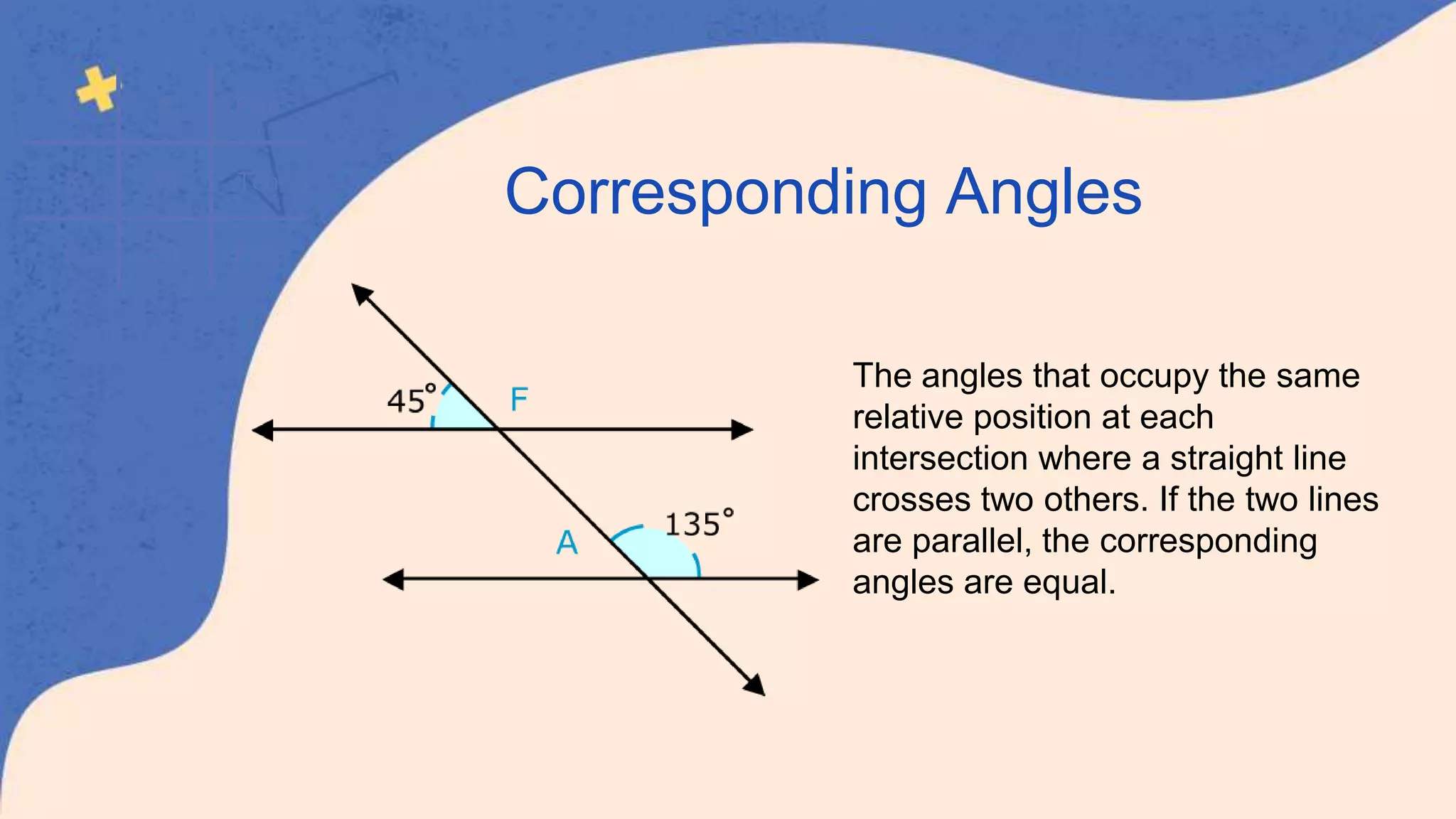
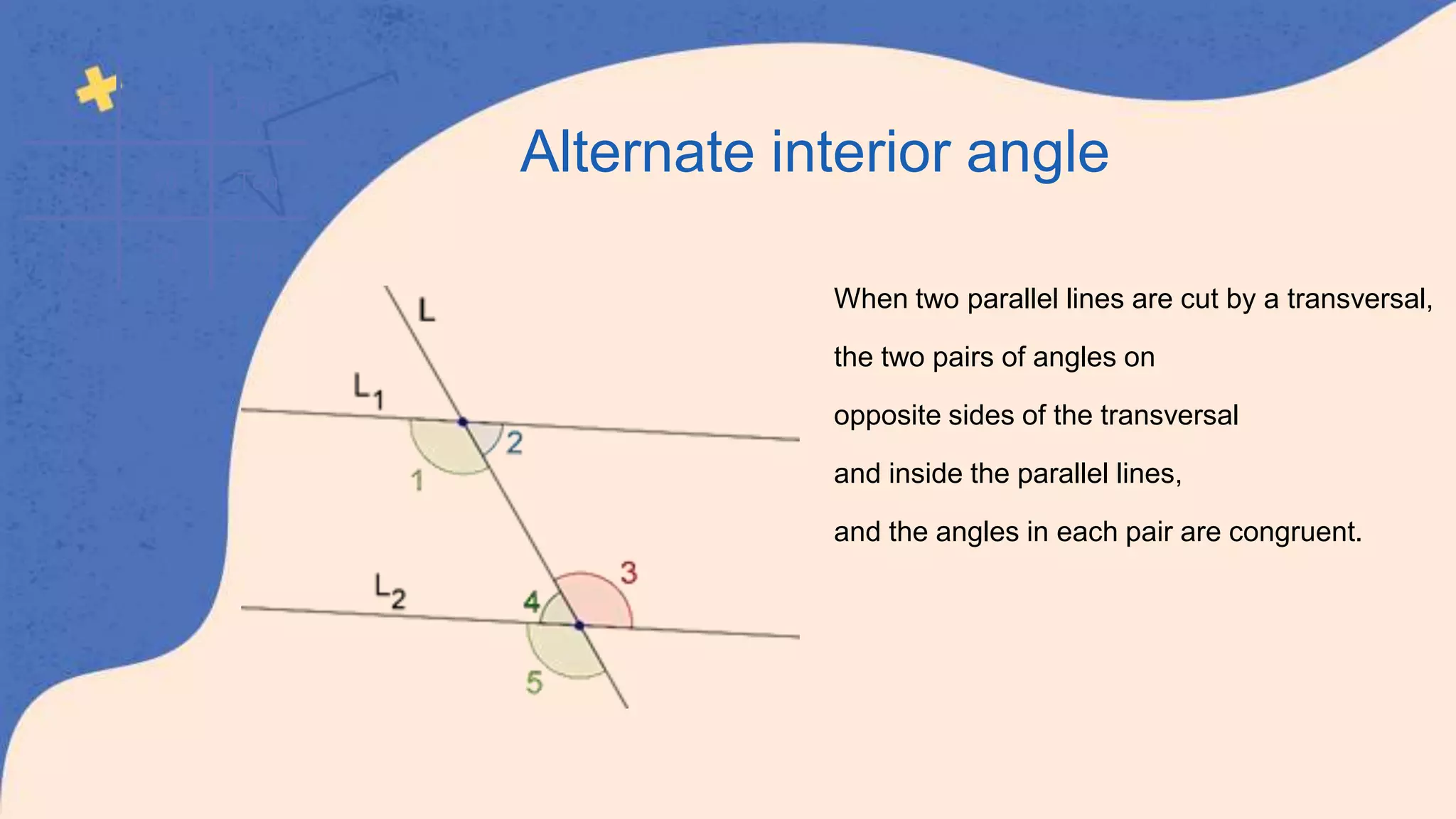
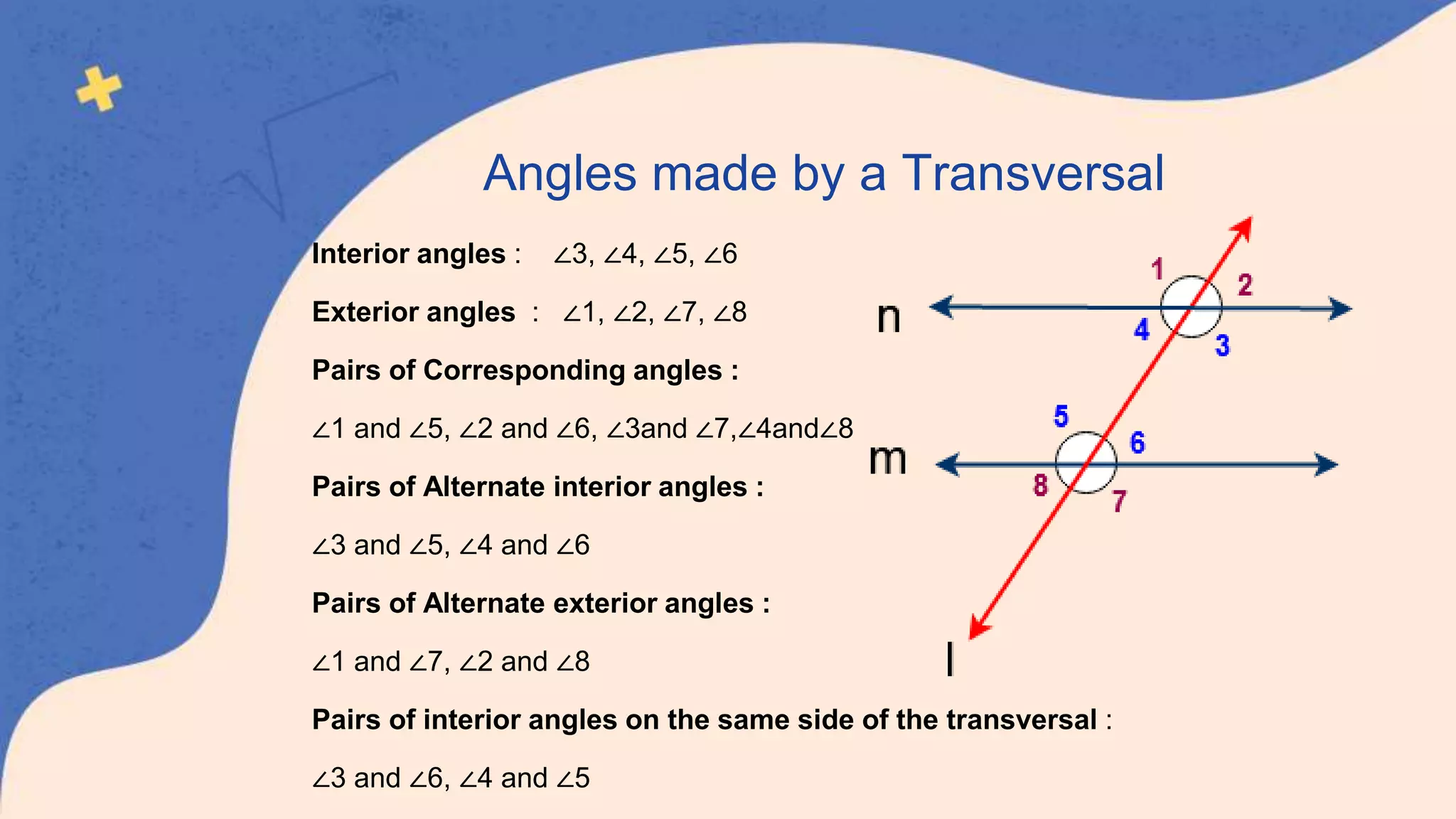
This document defines and classifies different types of angles, including acute, obtuse, right, straight, reflex, and complete angles. It describes how to measure angles using a protractor. Complementary angles and supplementary angles are defined as pairs of angles that sum to 90 and 180 degrees, respectively. Vertically opposite angles and corresponding angles formed by parallel lines crossed by a transversal are introduced. The relationships between interior angles, exterior angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of a transversal are also summarized.

1. LINES
&
ANGLES
Made By : RUBY SHARMA

2. 01
03
02
04
INTRODUCTION : ANGLES Classification of Angles
Lines Transversal line angles
Made By : RUBY SHARMA

3. Definition and Properties
Lines and Angles
Line segment : A line segment has two end points with a definite length.
Line : A straight path extending in both the directions with no end point.
Ray : Ray is a line with a single endpoint that extends infinitely in one direction.

4. V 5 Five
X 10 Ten
L 50 Fifty
A shape formed by two rays sharing a common endpoint.
Angle contains two rays and a vertex.
The magnitude of the angle is the "amount of rotation" that
separates the two rays, and can be measured by considering
the length of circular arc swept out when one ray is rotated
about the vertex to coincide with the other.
ray
ray
vertex
Ray—has one endpoint and goes
infinitely in one direction
Vertex—point common to two rays of
a triangle or two sides of a polygon
Angles

5. V 5 Five
X 10 Ten
L 50 Fifty
Measuring Angles
You measure angles with a protractor.
Thispointgoesatthevertexoftheangle
This
point is 0.
Notice there are two scales. Be careful which 0 you start at.
900

6. V 5 Five
X 10 Ten
L 50 Fifty
Types of Angles
□ Acute Angle: An angle whose measure is greater than
zero degrees and less than 90 degrees. A-cute=Small

7. □ One angle measures greater than 90 degrees and less than 180 degrees□ Obtuse angle

8. V 5 Five
X 10 Ten
L 50 Fifty
Right Angle
□ Angle that measures 90 degrees

9. V 5 Five
X 10 Ten
L 50 Fifty
Straight angle
A straight angle changes the direction to point the opposite way.
It looks like a straight line. It measures 180° (half a revolution, or two right angles)

10. Reflex Angle
Reflex angles are angles measuring greater than 180 degrees and less than 360 degrees.
The measure of a reflex angle is added to an acute or obtuse angle
to make a full 360 degree circle.

11. Complete Angle
□ Angle whose measure is equal to
1 Revolution = 1 Complete Angle
A Straight line makes an angle of 360
to reach its initial position completely by the rotation

12. Sum up —

13. V 5 Five
X 10 Ten
L 50 Fifty
What are complementary angles ?
Two angles are called Complementary angles if the sum of their degree
measurements equal 90 degree (right angle) One of the complementary
angle is said to be the complement of the other.
The two angles do not need to be together or adjacent they just need to
add up to 90 degrees.

14. V 5 Five
X 10 Ten
L 50 Fifty
What are Supplementary angles ?
Angles are Supplementary when they add up to 180 degrees.
A pair of adjacent angles formed by intersecting lines.
Linear pairs of angles are supplementary.

15. At both the vertices A and B, we find, a pair of angles are placed next
to each other. These angles are such that:
(i) they have a common vertex;
(ii) they have a common arm; and
(iii) vertex and a common arm but no common interior points.
the non-common arms are on either side of the common arm.
Adjacent Angle

16. V 5 Five
X 10 Ten
L 50 Fifty
a pair of angles is said to be vertical (also opposite and vertically opposite)
if the angles are formed from two intersecting lines and the angles are not adjacent.
They all share a vertex. Such angles are equal in measure and can be described as congruent.
Vertically Opposite angles
A
B

17. Transversal :- A transversal, or a line that intersects two or more
coplanar lines, each at a different point, is a very useful line in
geometry. Transversals tell us a great deal about angles.
Parallel Lines :- Parallel lines remain the same distance apart
over their entire length. No matter how far you extend them, they
will never meet.
• Corresponding Angles : 6, 2 & 5,1
• Alternate Interior Angles : 5,4 & 6,3
• Alternate Exterior Angles :
• Interior Angles on same side of the transversal
Transversal
& parallel
lines

18. V 5 Five
X 10 Ten
L 50 Fifty
The angles that occupy the same
relative position at each
intersection where a straight line
crosses two others. If the two lines
are parallel, the corresponding
angles are equal.
Corresponding Angles

19. V 5 Five
X 10 Ten
L 50 Fifty
When two parallel lines are cut by a transversal,
the two pairs of angles on
opposite sides of the transversal
and inside the parallel lines,
and the angles in each pair are congruent.
Alternate interior angle

20. A linear pair is a pair of adjacent angles whose non-common sides are opposite rays.
A pen stand :The pen makes a linear pair of angles with the stand.
Linear Pair

21. Interior angles : ∠3, ∠4, ∠5, ∠6
Exterior angles : ∠1, ∠2, ∠7, ∠8
Pairs of Corresponding angles :
∠1 and ∠5, ∠2 and ∠6, ∠3and ∠7,∠4and∠8
Pairs of Alternate interior angles :
∠3 and ∠5, ∠4 and ∠6
Pairs of Alternate exterior angles :
∠1 and ∠7, ∠2 and ∠8
Pairs of interior angles on the same side of the transversal :
∠3 and ∠6, ∠4 and ∠5
Angles made by a Transversal

22. Thank You