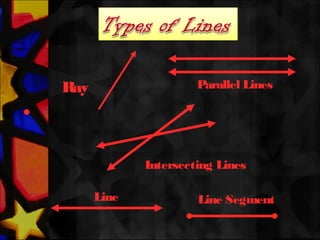
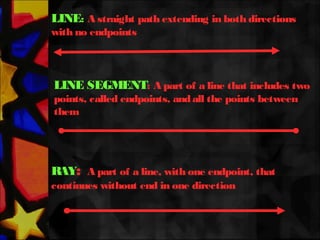
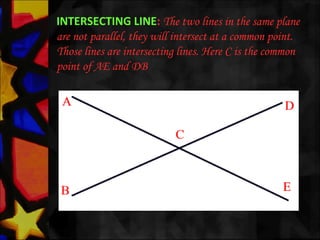
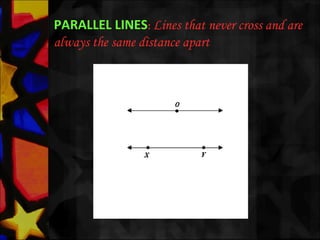
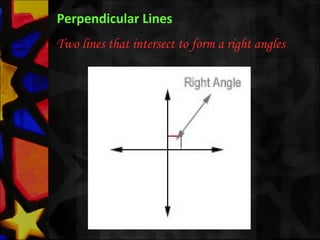
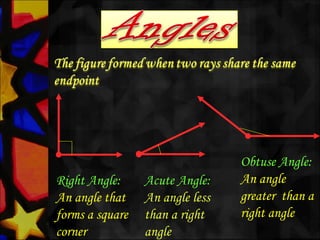
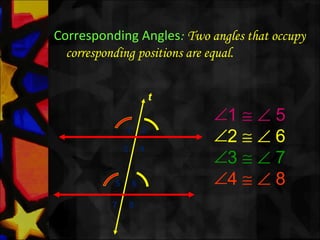
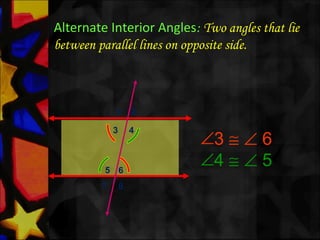
This document defines and describes various types of angles and lines. It defines a ray, line, and line segment. It describes intersecting lines, parallel lines, perpendicular lines, and types of angles such as acute, obtuse, straight, reflex, complementary, supplementary, vertical, and linear pairs. It also defines terms like transversal, corresponding angles, interior angles, exterior angles, and proves properties such as vertically opposite angles being equal and the angle sum of a triangle being 180 degrees.

2. Ray
Line
Intersecting Lines
Parallel Lines
Line Segment

3. RAY: A part of a line, with one endpoint, that
continues without end in one direction
LINE: A straight path extending in both directions
with no endpoints
LINE SEGMENT: A part of a line that includes two
points, called endpoints, andall the points between
them

4. INTERSECTING LINE: The two lines in the same plane
are not parallel, they will intersect at a common point.
Those lines are intersecting lines. Here C is the common
point of AE and DB

5. PARALLEL LINES: Lines that never cross and are
always the same distance apart

6. Perpendicular Lines
Two lines that intersect to form a right angles

7. Right Angle:
An angle that
forms a square
corner
Acute Angle:
An angle less
than a right
angle
Obtuse Angle:
An angle
greater than a
right angle

8. Straight Angle: It is equal to 180°
Reflex Angle: An angle which is more than 180° but
less than 360°

9. Complementary Angles: Two angles adding up to
90° are called complementary angles.
Here ABD + DBC are
Complementary.

10. Supplementary Angles: Two angles adding up to
180° are called supplementary.
ABD + DBC are supplementary

11. Transversal: A Transversal is a line that
intersect two parallel lines at different points.

12. Vertical Angles: Two angles that are opposite
angles
1 2
3 4
5 6
7 8
t
∠1 ≅ ∠ 4
∠2 ≅ ∠ 3
∠5 ≅ ∠ 8
∠6 ≅ ∠ 7

13. Linear Pair: Two angles that form a line
(sum=180°)
1 2
3 4
5 6
7 8
t
∠5+∠6=180
∠6+∠8=180
∠8+∠7=180
∠7+∠5=180
∠1+∠2=180
∠2+∠4=180
∠4+∠3=180
∠3+∠1=180

14. Corresponding Angles: Two angles that occupy
corresponding positions are equal.
∠1 ≅ ∠ 5
∠2 ≅ ∠ 6
∠3 ≅ ∠ 7
∠4 ≅ ∠ 8
t
1 2
3 4
5 6
7 8

15. Alternate Interior Angles: Two angles that lie
between parallel lines on opposite side.
∠3 ≅ ∠ 6
∠4 ≅ ∠ 5
1 2
3 4
5 6
7 8

16. Co-Interior Angles: Two angles that lie between
parallel lines on the same side of the transversal
1 2
3 4
5 6
7 8
3 +∠5 = 180
4 +∠6 = 180

17. Alternate Exterior Angles: Two angles that lie
outside parallel lines on opposite sides of the
transversal
1 2
3 4
5 6
7 8
2 ≅ ∠ 7
1 ≅ ∠ 8

18. Angle Sum Property Of Triangle: The sum of the
angles of a triangle is 180°.
1
23
1 + 2 + 3 = 180°

19. Property of Exterior Angle: If a side of a triangle is
produced, then the exterior angle so formed is equal to the
sum of the two interior opposite angles.
Angle 1,2,3
are exterior
angles of
triangle

20. • Vertically Opposite Angles are equal
To Proof – Vertically Opposite Angles are equal

21. Solution - ∠b + ∠n = 180° ( LINEAR PAIR)
∠b + ∠m = 180° ( LINEAR PAIR)
EQUATING BOTH THE EQUATIONS
→ ∠b + ∠n = ∠b + ∠m
→ ∠n = ∠m
Hence Proved

22. • Angle Sum Property Of A Triangle is 180°
To Proof -Angle Sum Property Of a Triangle is
180°
Construction - Draw ↔m parallel to BC
Solution - ∠4 = ∠1 (Alternate Interior Angles)
∠5 = ∠2 (Alternate Interior Angles)

23. ∠3 + ∠4 + ∠5 = 180° ( Angles on the same line are
supplementary)
Substituting the values
∠3 + ∠1 + ∠2 = 180° (Angle Sum Property)
Hence Proved

24. Made by:
Shaik Mallika