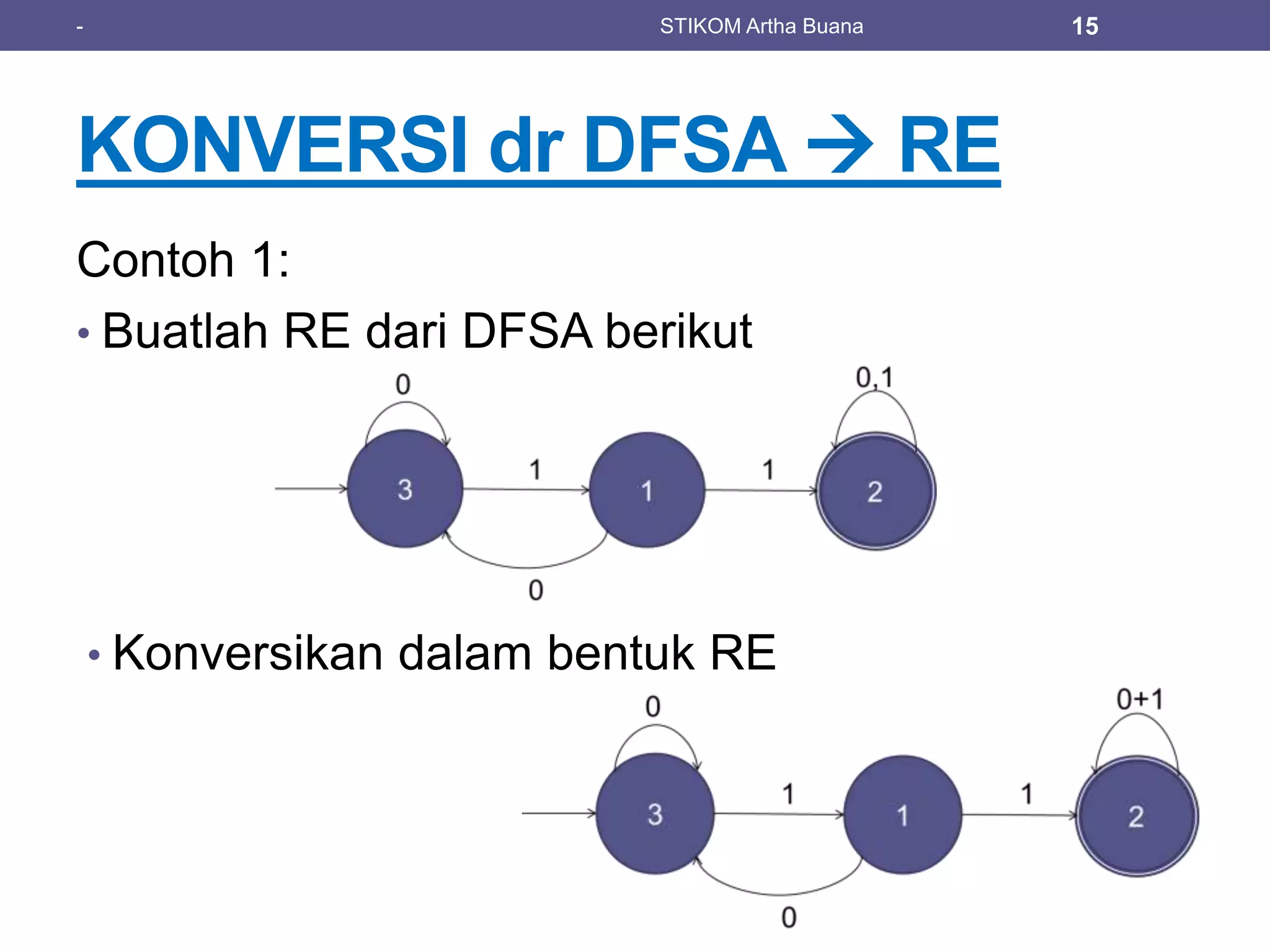
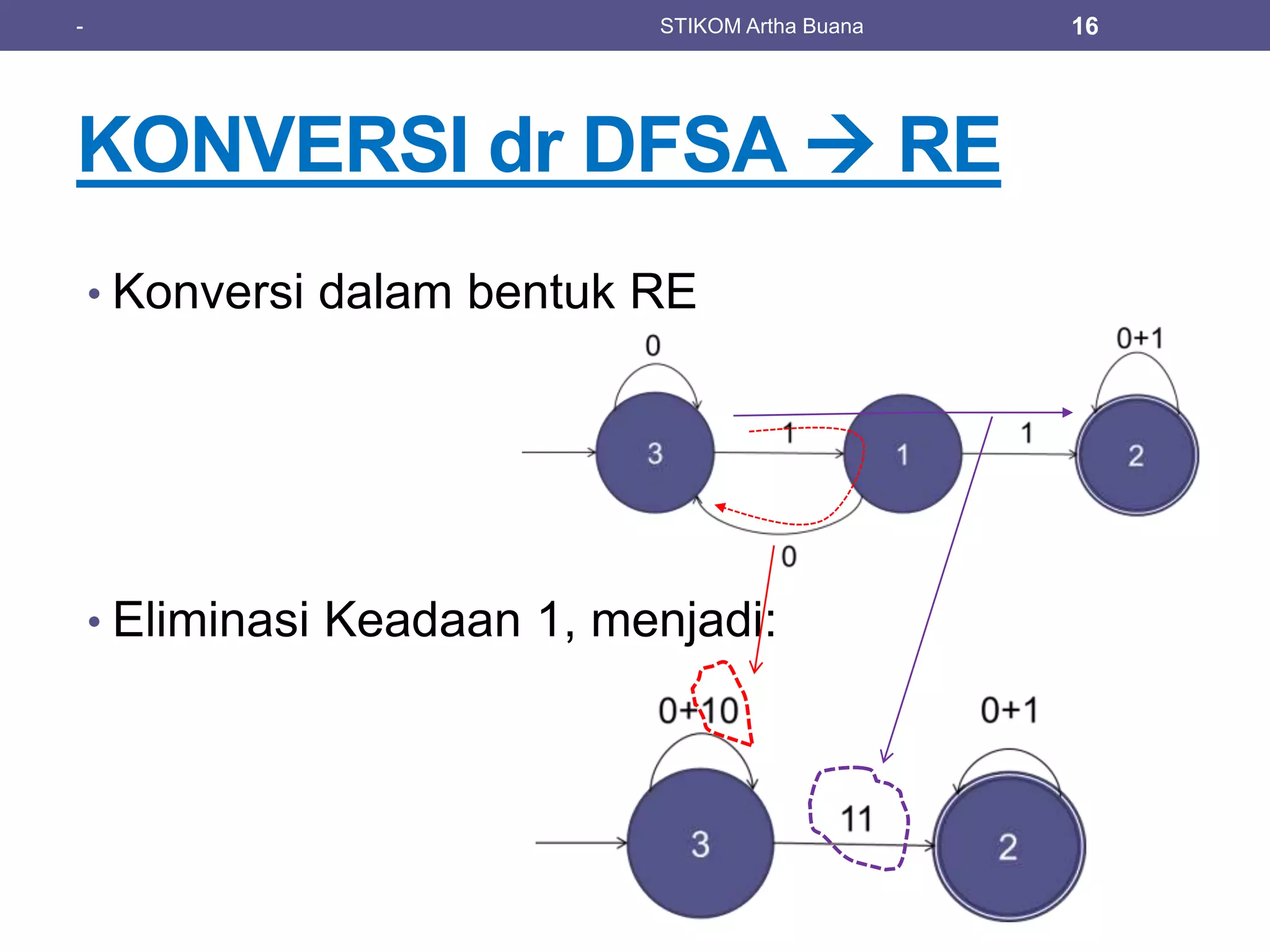
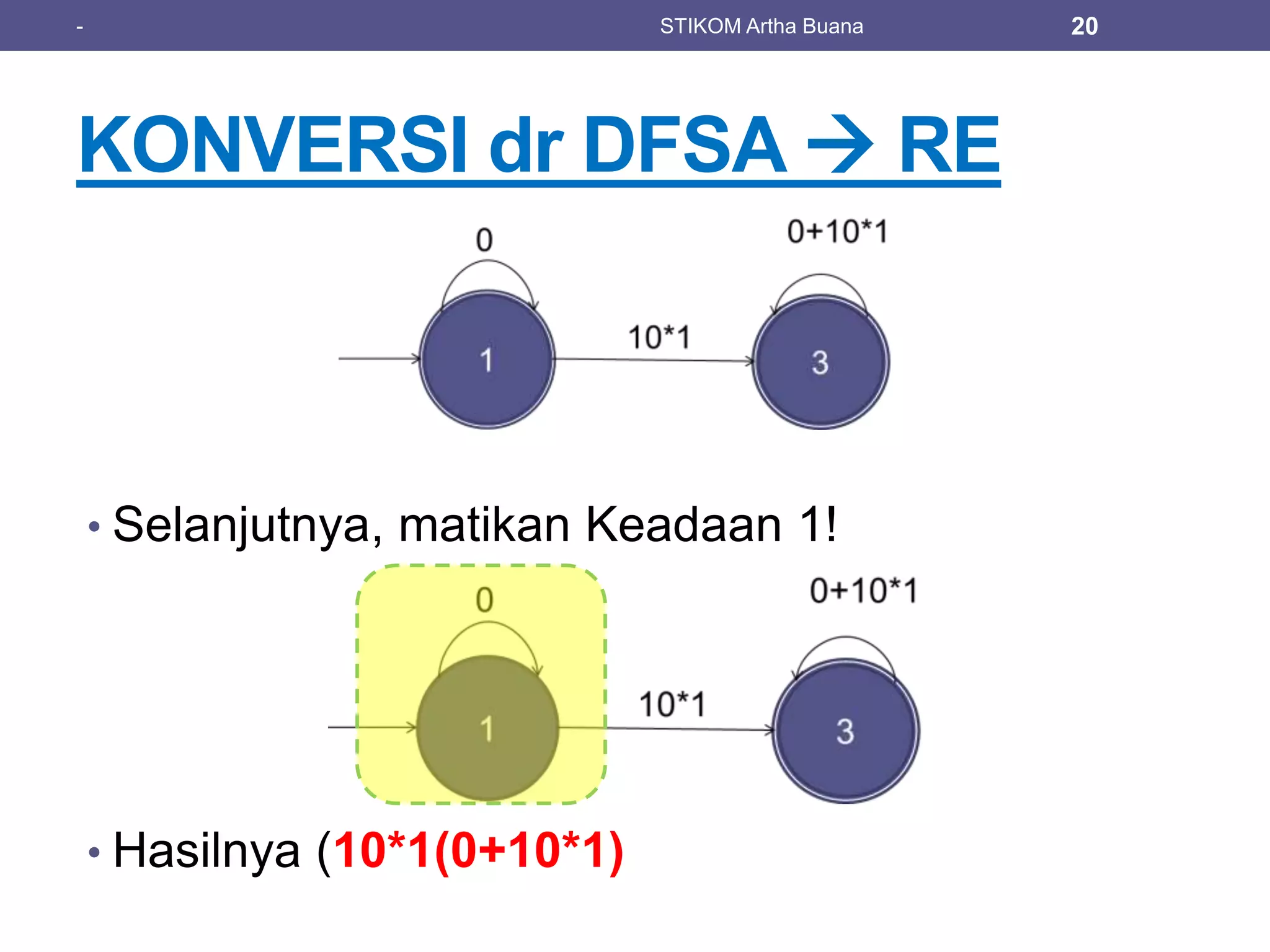
The document discusses regular expressions (regex) and their relation to finite automata and regular languages, providing definitions and examples. It covers operations such as union, concatenation, and closure, alongside various examples of regular expressions. Additionally, it explains the process of converting deterministic finite state automata (DFSA) to regular expressions with practical examples.

1. REGEX (REGULAR EXPRESSION)
STIKOM Artha Buana
Teknik Informatika
2014
Ir. Ahmad Haidaroh, M.Kom.

2. Regular expressions
• FSA (NFSA atau DFSA) merupakan cetak biru
(blueprint) untuk membuat suatu mesin yang
dapat mengenali regular language (RL).
• Regex merupakan cara pendeklarasian RL
yang ramah pengguna (user-friendly).
• Contoh: 01* + 10*
- 2
STIKOM Artha Buana

3. Regular expressions
• Regex digunakan, misalnya pada:
• Perintah grep UNIX
• Tools Lex (Lexical analyzer generator) dan
Flex (Fast Lex) UNIX
- 3
STIKOM Artha Buana

4. • Regular Language Finite Automata
• Regular Language  Regular Expressions
• Finite Automata  Regular Expressions
- 4
STIKOM Artha Buana

5. • Regular Language Finite Automata
• Regular Language  Regular Expressions
• Finite Automata  Regular Expressions
- 5
STIKOM Artha Buana

6. • Regular Language Finite Automata
• Regular Language  Regular Expressions
• Finite Automata  Regular Expressions
- 6
STIKOM Artha Buana

7. Review (Operasi Bahasa)
• Gabungan (Union)
L  M = {w | w  L atau w  M}
• Sambungan (Konkatenasi)
LM = {w | w = xy, x  L atau y  M}
• Pangkat
L0 = {}, L1= L, Lk+1= LLk
• Klosur
L* = 𝑖=0
∞
𝐿𝑖
- 7
STIKOM Artha Buana
x = 01101 dan y = 110
Maka xy = 01101110 dan yx = 11001101
Jika L = {001, 10, 111} dan M = {, 001} maka
L.M = {001, 10, 111, 001001, 10001, 111001}

8. Regular
Language
Regular Language & Regular Expressions
Contoh 1:
r = (a + b.c)*
L(r) = {a,bc}*
L(r) = {, a, bc, aa, abc, bca, …}
- 8
STIKOM Artha Buana
Regular Expressions

9. Regular Language & Regular Expressions
Contoh 2:
r = (a + b)*(a + bb)
L(r) = {a, bb, aa, abb, ba, bbb, …}
- 9
STIKOM Artha Buana

10. Regular Language & Regular Expressions
Contoh 3:
r = (aa)*(bb)*b
L(r) = {a2nb2mb | n,m ≥ 1}
- 10
STIKOM Artha Buana

11. Regular Language & Regular Expressions
Contoh 4:
r = (aa)*(bb)*b
L(r) = {a2nb2mb | n,m ≥ 0}
- 11
STIKOM Artha Buana

12. Regular Language & Regular Expressions
Contoh 5:
r = (0+1)*00(0+1)*
L(r) = {semua string yang memiliki
sekurangnya dua 0 berurutan}
- 12
STIKOM Artha Buana

13. Regular Language & Regular Expressions
Contoh 6:
r = (1+01)*(0+)
L(r) = {semua string tanpa dua 0
berurutan}
)
0
(
*
)
01
1
( 



r
- 13
STIKOM Artha Buana

14. • Regular Language Finite Automata
• Regular Language  Regular Expressions
• Finite Automata  Regular Expressions
- 14
STIKOM Artha Buana

15. KONVERSI dr DFSA  RE
Contoh 1:
• Buatlah RE dari DFSA berikut
• Konversikan dalam bentuk RE
- 15
STIKOM Artha Buana

16. • Eliminasi Keadaan 1, menjadi:
• Konversi dalam bentuk RE
- 16
STIKOM Artha Buana
KONVERSI dr DFSA  RE

17. • RE dari DFSA : (0+10)*11(0+1)*
• Eliminasi Keadaan 1
- 17
STIKOM Artha Buana
Ingat ! : State Input dan Output harus selalu ada
KONVERSI dr DFSA  RE

18. Contoh 2:
• Buatlah RE dari DFSA yang dapat menerima 1
berjumlah genap
• Eliminasi Keadaan 2, menjadi
- 18
STIKOM Artha Buana
0+10*1
KONVERSI dr DFSA  RE

19. • Dua keadaan akhir, matikan Keadaan 3 dahulu!
• Hasilnya 0* karena yang menuju Keadaan 3 tidak
akan diterima FSA (seharusnya finish di 3)
- 19
STIKOM Artha Buana
0+10*1
KONVERSI dr DFSA  RE

20. • Selanjutnya, matikan Keadaan 1!
• Hasilnya (10*1(0+10*1)
- 20
STIKOM Artha Buana
KONVERSI dr DFSA  RE

21. • Dikombinasikan dengan hasil sebelumnya,
menjadi: (0*+10*1(0+10*1)
- 21
STIKOM Artha Buana
KONVERSI dr DFSA  RE