Downloaded 10 times
![Reinforcement Learning – Q Learning
17
Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all
actions)]
http://mnemstudio.org/path-finding-q-learning-tutorial.htm
Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)]](https://image.slidesharecdn.com/pydatareinforcementlearning-190421043127/85/Machine-learning-Vs-Deep-learning-Vs-Reinforcement-learning-Pydata-Mumbai-17-320.jpg)
![Reinforcement Learning – Q Learning
18
http://mnemstudio.org/path-finding-q-learning-tutorial.htm
Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)]](https://image.slidesharecdn.com/pydatareinforcementlearning-190421043127/85/Machine-learning-Vs-Deep-learning-Vs-Reinforcement-learning-Pydata-Mumbai-18-320.jpg)
Uploaded byPratik Bhavsar
Machine learning Vs Deep learning Vs Reinforcement learning | Pydata Mumbai
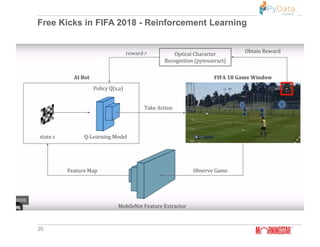
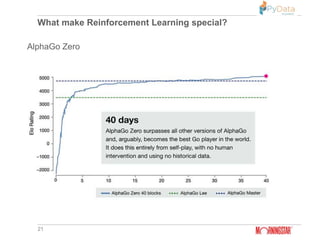
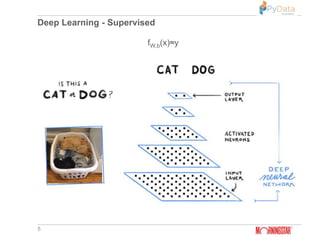
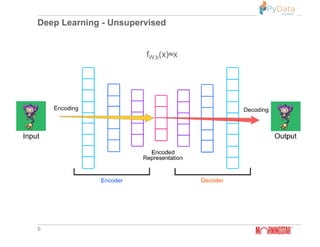
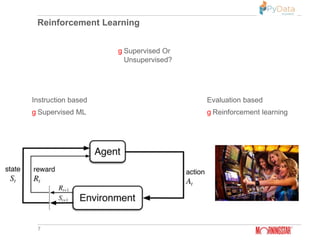
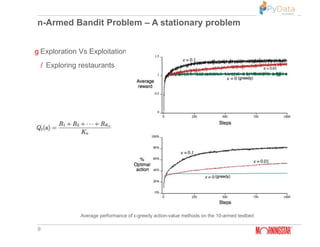
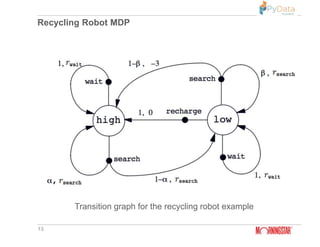
The document summarizes Pratik Bhavsar's presentation at the PyData Meetup 11 in Mumbai on August 11, 2018. The presentation covered the differences between machine learning, deep learning, and reinforcement learning. It provided examples of supervised and unsupervised deep learning and discussed the n-armed bandit problem and reinforcement learning tasks. Key concepts from reinforcement learning like the Markov property, value functions, Q-learning, and applications were also summarized. The presentation concluded with an example of using reinforcement learning for free kicks in the FIFA 2018 video game.
Machine learning Vs Deep learning Vs Reinforcement learning | Pydata Mumbai
- 1. PyData Meetup 11, Mumbai,Aug 11, 2018 Pratik Bhavsar Senior Data Scientist Morningstar Dog Vs Labrador Vs German Shepherd
- 2. Dog Vs LabradorVs German Shepherd Machine Learning Vs Deep Learning Vs Reinforcement Learning
- 3.
- 4. Deep Learning 4 g Universalapproximation theorem g XOR function
- 5. Deep Learning -Supervised 5 fW,b(x)≈y
- 6. Deep Learning -Unsupervised 6 fW,b(x)≈x
- 7. Reinforcement Learning 7 g SupervisedOr Unsupervised? Instruction based g Supervised ML Evaluation based g Reinforcement learning
- 8. n-Armed Bandit Problem– A stationary problem 8 g Exploration Vs Exploitation Average performance of ε-greedy action-value methods on the 10-armed testbed Agent’s goal is to maximize the reward it receives in the long run. How might this be formally defined?
- 9. n-Armed Bandit Problem– A stationary problem 9 g Exploration Vs Exploitation / Exploring restaurants Average performance of ε-greedy action-value methods on the 10-armed testbed
- 10. Reinforcement Learning Tasks 10 gEpisodic tasks / Mario g Continuous tasks / pubg
- 11. The Markov Property 11 gA stochastic process has the Markov property if the conditional probability distribution of future states of the process (conditional on both past and present states) depends only upon the present state, not on the sequence of events that preceded it. g TLDR: Future can be predicted by just the present state. History is irrelevant.
- 12. Recycling Robot MDP 12 1.Actively search for a can 2. Remain stationary and wait for someone to bring it a can 3. Go back to home base to recharge its battery. A(high) = {search, wait} A(low) = {search, wait, recharge}
- 13. Recycling Robot MDP 13 Transitiongraph for the recycling robot example
- 14. Value functions 14 g Valuefunction = state–action pairs / Predict how good it is for the agent to perform a given action in a given state / Goodness is defined in terms of future reward that can be expected State-action function for policy π State-value function for policy πChoosing career What to do after B.Tech? Reward of B.Tech
- 15.
- 16. Reinforcement Learning –Q Learning 16
- 17. Reinforcement Learning –Q Learning 17 Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)] http://mnemstudio.org/path-finding-q-learning-tutorial.htm Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)]
- 18. Reinforcement Learning –Q Learning 18 http://mnemstudio.org/path-finding-q-learning-tutorial.htm Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)]
- 19. Reinforcement Learning 19 g Applications /Finance / Game Theory and Multi-Agent Interaction / Robotics / Vehicular Navigation
- 20. Free Kicks inFIFA 2018 - Reinforcement Learning 20
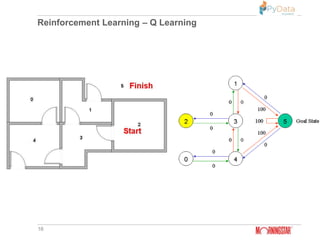
- 21. What make ReinforcementLearning special? 21 AlphaGo Zero
- 22.
Editor's Notes
- #7 The autoencoder tries to learn a function fW,b(x)≈x. In other words, it is trying to learn an approximation to the identity function, so as to output x̂ that is similar to x. The identity function seems a particularly trivial function to be trying to learn; but by placing constraints on the network, such as by limiting the number of hidden units, we can discover interesting structure about the data. As a concrete example, suppose the inputs x are the pixel intensity values from a 10×10 image (100 pixels) so n=100, and there are s2=50 hidden units in layer L2. Note that we also have y∈ℜ100. Since there are only 50 hidden units, the network is forced to learn a ”compressed” representation of the input. I.e., given only the vector of hidden unit activations a(2)∈ℜ50a(2), it must try to ”‘reconstruct”’ the 100-pixel input x. If the input were completely random—say, each xi comes from an IID Gaussian independent of the other features—then this compression task would be very difficult. But if there is structure in the data, for example, if some of the input features are correlated, then this algorithm will be able to discover some of those correlations. In fact, this simple autoencoder often ends up learning a low-dimensional representation very similar to PCAs.
- #8 Reinforcement learning 1) A human builds an algorithm based on input data 2) That algorithm presents a state dependent on the input data in which a user rewards or punishes the algorithm via the action the algorithm took, this continues over time 3) That algorithm learns from the reward/punishment and updates itself, this continues 4) It's always in production, it needs to learn real data to be able to present actions from states Supervised vs Reinforcement Learning: In supervised learning, there’s an external “supervisor”, which has knowledge of the environment and who shares it with the agent to complete the task. But there are some problems in which there are so many combinations of subtasks that the agent can perform to achieve the objective. So that creating a “supervisor” is almost impractical. For example, in a chess game, there are tens of thousands of moves that can be played. So creating a knowledge base that can be played is a tedious task. In these problems, it is more feasible to learn from one’s own experiences and gain knowledge from them. This is the main difference that can be said of reinforcement learning and supervised learning. In both supervised and reinforcement learning, there is a mapping between input and output. But in reinforcement learning, there is a reward function which acts as a feedback to the agent as opposed to supervised learning. Unsupervised vs Reinforcement Leanring: In reinforcement learning, there’s a mapping from input to output which is not present in unsupervised learning. In unsupervised learning, the main task is to find the underlying patterns rather than the mapping. For example, if the task is to suggest a news article to a user, an unsupervised learning algorithm will look at similar articles which the person has previously read and suggest anyone from them. Whereas a reinforcement learning algorithm will get constant feedback from the user by suggesting few news articles and then build a “knowledge graph” of which articles will the person like.
- #9 The simplest action selection rule is to select the action (or one of the actions) with highest estimated action value, that is, to select at step t one of the greedy actions, A∗t , for which Qt(A∗t ) = maxa Qt(a). This method always exploits current knowledge to maximize immediate reward; it spends no time at all sampling apparently inferior actions to see if they might really be better. A simple alternative is to behave greedily most of the time, but every once in a while, say with small probability ε, instead to select randomly from amongst all the actions with equal probability independently of the action- value estimates. We call methods using this near-greedy action selection rule ε-greedy methods. An advantage of these methods is that, in the limit as the number of plays increases, every action will be sampled an infinite number of times, guaranteeing that Ka → ∞ for all a, and thus ensuring that all the Qt(a) converge to q∗(a). This of course implies that the probability of selecting the optimal action converges to greater than 1 − ε, that is, to near certainty. The ε-greedy methods eventually perform better because they continue to explore, and to improve their chances of recognizing the optimal action. The ε = 0.1 method explores more, and usually finds the optimal action earlier, but never selects it more than 91% of the time. The ε = 0.01 method improves more slowly, but eventually performs better than the ε = 0.1 method on both performance measures. It is also possible to reduce ε over time to try to get the best of both high and low values.
- #10 The simplest action selection rule is to select the action (or one of the actions) with highest estimated action value, that is, to select at step t one of the greedy actions, A∗t , for which Qt(A∗t ) = maxa Qt(a). This method always exploits current knowledge to maximize immediate reward; it spends no time at all sampling apparently inferior actions to see if they might really be better. A simple alternative is to behave greedily most of the time, but every once in a while, say with small probability ε, instead to select randomly from amongst all the actions with equal probability independently of the action- value estimates. We call methods using this near-greedy action selection rule ε-greedy methods. An advantage of these methods is that, in the limit as the number of plays increases, every action will be sampled an infinite number of times, guaranteeing that Ka → ∞ for all a, and thus ensuring that all the Qt(a) converge to q∗(a). This of course implies that the probability of selecting the optimal action converges to greater than 1 − ε, that is, to near certainty. The ε-greedy methods eventually perform better because they continue to explore, and to improve their chances of recognizing the optimal action. The ε = 0.1 method explores more, and usually finds the optimal action earlier, but never selects it more than 91% of the time. The ε = 0.01 method improves more slowly, but eventually performs better than the ε = 0.1 method on both performance measures. It is also possible to reduce ε over time to try to get the best of both high and low values.
- #12 Draw Poker In draw poker, each player is dealt a hand of five cards. There is a round of betting, in which each player exchanges some of his cards for new ones, and then there is a final round of betting. At each round, each player must match or exceed the highest bets of the other players, or else drop out (fold). After the second round of betting, the player with the best hand who has not folded is the winner and collects all the bets. The state signal in draw poker is different for each player. Each player knows the cards in his own hand, but can only guess at those in the other players’ hands. A common mistake is to think that a Markov state signal should include the contents of all the players’ hands and the cards remaining in the deck. In a fair game, however, we assume that the players are in principle unable to determine these things from their past observations. If a player did know them, then she could predict some future events (such as the cards one could exchange for) better than by remembering all past observations. In addition to knowledge of one’s own cards, the state in draw poker should include the bets and the numbers of cards drawn by the other players. For example, if one of the other players drew three new cards, you may suspect he retained a pair and adjust your guess of the strength of his hand accordingly. The players’ bets also influence your assessment of their hands. In fact, much of your past history with these particular players is part of the Markov state. Does Ellen like to bluff, or does she play conservatively? Does her face or demeanor provide clues to the strength of her hand? How does Joe’s play change when it is late at night, or when he has already won a lot of money? Although everything ever observed about the other players may have an effect on the probabilities that they are holding various kinds of hands, in practice this is far too much to remember and analyze, and most of it will have no clear effect on one’s predictions and decisions. Very good poker players are adept at remembering just the key clues, and at sizing up new players quickly, but no one remembers everything that is relevant. As a result, the state representations people use to make their poker decisions are undoubtedly non- Markov, and the decisions themselves are presumably imperfect. Nevertheless, people still make very good decisions in such tasks. We conclude that the inability to have access to a perfect Markov state representation is probably not a severe problem for a reinforcement learning agent. Pole-Balancing State In the pole-balancing task intro- duced earlier, a state signal would be Markov if it specified exactly, or made it possible to reconstruct exactly, the position and velocity of the cart along the track, the angle between the cart and the pole, and the rate at which this angle is changing (the angular velocity). In an idealized cart–pole system, this information would be sufficient to exactly predict the future behavior of the cart and pole, given the actions taken by the controller. In practice, however, it is never possible to know this information exactly because any real sensor would introduce some distortion and delay in its measurements. Furthermore, in any real cart–pole system there are always other effects, such as the bend- ing of the pole, the temperatures of the wheel and pole bearings, and various forms of backlash, that slightly affect the behavior of the system. These factors would cause violations of the Markov property if the state signal were only the positions and velocities of the cart and the pole. However, often the positions and velocities serve quite well as states. Some early studies of learning to solve the pole-balancing task used a coarse state signal that divided cart positions into three regions: right, left, and middle (and similar rough quantizations of the other three intrinsic state variables). This distinctly non-Markov state was sufficient to allow the task to be solved easily by reinforcement learning methods. In fact, this coarse representation may have facilitated rapid learning by forcing the learning agent to ignore fine distinctions that would not have been useful in solving the task.
- #17 Suppose we have 5 rooms in a building connected by doors as shown in the figure below. We'll number each room 0 through 4. The outside of the building can be thought of as one big room (5). Notice that doors 1 and 4 lead into the building from room 5 (outside). We can represent the rooms on a graph, each room as a node, and each door as a link.
- #18 For this example, we'd like to put an agent in any room, and from that room, go outside the building (this will be our target room). In other words, the goal room is number 5. To set this room as a goal, we'll associate a reward value to each door (i.e. link between nodes). The doors that lead immediately to the goal have an instant reward of 100. Other doors not directly connected to the target room have zero reward. Because doors are two-way ( 0 leads to 4, and 4 leads back to 0 ), two arrows are assigned to each room. Of course, Room 5 loops back to itself with a reward of 100, and all other direct connections to the goal room carry a reward of 100. In Q-learning, the goal is to reach the state with the highest reward, so that if the agent arrives at the goal, it will remain there forever. This type of goal is called an "absorbing goal". Imagine our agent as a dumb virtual robot that can learn through experience. The agent can pass from one room to another but has no knowledge of the environment, and doesn't know which sequence of doors lead to the outside. Suppose we want to model some kind of simple evacuation of an agent from any room in the building. Now suppose we have an agent in Room 2 and we want the agent to learn to reach outside the house (5). More on http://mnemstudio.org/path-finding-q-learning-tutorial.htm
- #19 Once the matrix Q gets close enough to a state of convergence, we know our agent has learned the most optimal paths to the goal state. Tracing the best sequences of states is as simple as following the links with the highest values at each state.