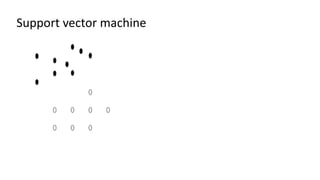
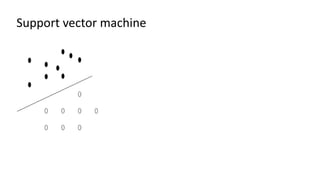
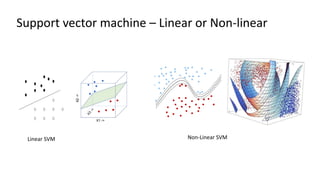
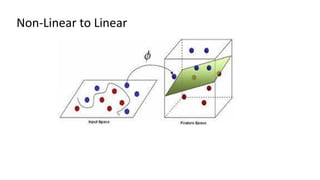
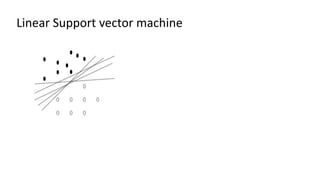
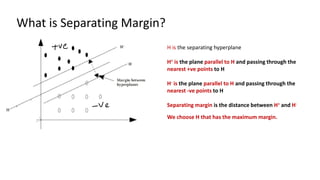
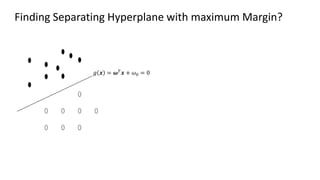
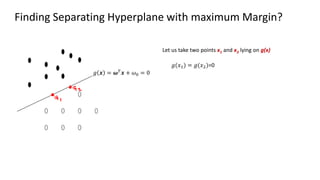
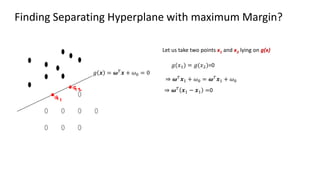
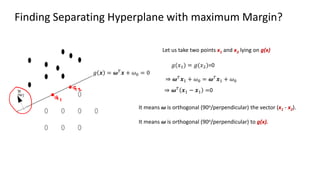
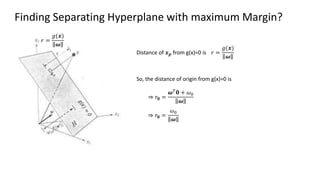
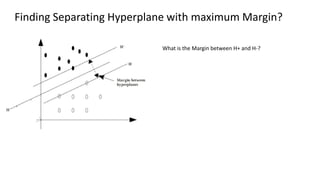
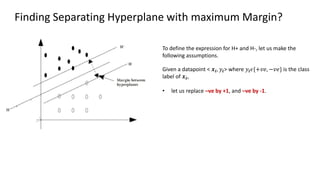
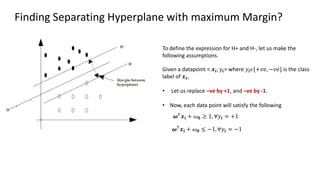
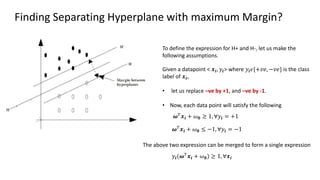
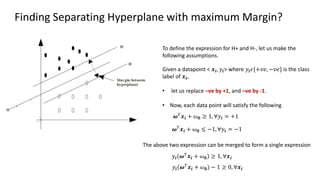
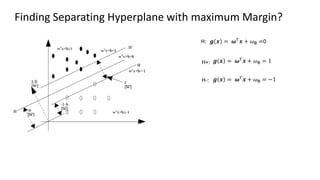
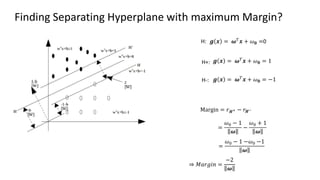
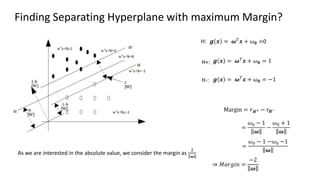
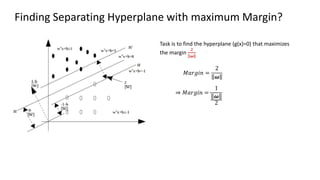
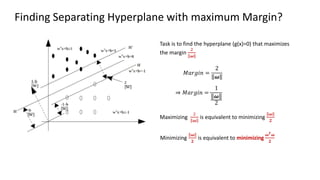
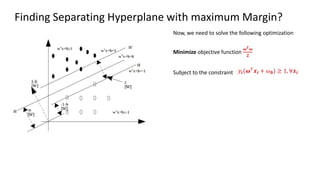
The document discusses support vector machines (SVM), detailing their linear and non-linear classifications and the concept of the separating hyperplane. It explains how to find the hyperplane with the maximum separating margin, defining key terms such as margin and support vectors, and outlines the optimization problem to determine parameters for classification. The document also includes mathematical formulations and constraints necessary for implementing SVM.

2. Lesson 6
Support vector machine (SVM)

3. Support vector machine

4. Support vector machine

5. Support vector machine

6. Support vector machine

7. Support vector machine – Linear or Non-linear
Linear SVM Non-Linear SVM

8. Non-Linear to Linear

9. Linear Support vector machine

10. Linear Support vector machine

11. Linear Support vector machine
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0
For all the points on the hyper plane, g(x) = 0

12. Linear Support vector machine
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 > 0
For all the points above the hyper plane, g(x) > 0

13. Linear Support vector machine
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 < 0
For all the points below the hyper plane, g(x) < 0

14. Linear Support vector machine
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 < 0
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 > 0
We choose the hyperplane that has
the maximum separating margin

15. What is Separating Margin?
H is the separating hyperplane
H+ is the plane parallel to H and passing through the
nearest +ve points to H
H- is the plane parallel to H and passing through the
nearest -ve points to H
Separating margin is the distance between H+ and H-
We choose H that has the maximum margin.

16. Finding Separating Hyperplane with maximum Margin?
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0

17. Finding Separating Hyperplane with maximum Margin?
Let us take two points x1 and x2 lying on g(x)
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0
𝑔(𝑥1) = 𝑔(𝑥2)=0

18. Finding Separating Hyperplane with maximum Margin?
Let us take two points x1 and x2 lying on g(x)
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0
𝑔(𝑥1) = 𝑔(𝑥2)=0
⇒ 𝝎𝑇
𝒙1 + 𝜔0 = 𝝎𝑇
𝒙1 + 𝜔0
⇒ 𝝎𝑇 𝒙1 − 𝒙1 =0

19. Finding Separating Hyperplane with maximum Margin?
Let us take two points x1 and x2 lying on g(x)
𝑔 𝒙 = 𝝎𝑇
𝒙 + 𝜔0 = 0
𝑔(𝑥1) = 𝑔(𝑥2)=0
⇒ 𝝎𝑇
𝒙1 + 𝜔0 = 𝝎𝑇
𝒙1 + 𝜔0
⇒ 𝝎𝑇 𝒙1 − 𝒙1 =0
It means 𝝎 is orthogonal (90o/perpendicular) the vector (x1 - x2).
It means 𝝎 is orthogonal (90o/perpendicular) to g(x).

20. Finding Separating Hyperplane with maximum Margin?
Let x be a point in space.
Let r be the distance of the point x from the hyperplane g(x),
and xp be the corresponding projection point of x on g(x).
Now, vector 𝒙 can be defined by the sum of the vector 𝒙𝒑 and vector 𝒓.
𝒙 = 𝒙𝒑 + 𝒓
⇒ 𝒙 = 𝒙𝒑 + 𝑟
𝝎
𝝎

21. Finding Separating Hyperplane with maximum Margin?
Let x be a point in space.
Let r be the distance of the point x from the hyperplane g(x),
and xp be the corresponding projection point of x on g(x).
Now, vector 𝒙 can be defined by the sum of the vector 𝒙𝒑 and vector 𝒓.
𝒙 = 𝒙𝒑 + 𝒓
⇒ 𝒙 = 𝒙𝒑 + 𝑟
𝝎
𝝎
If you substitute 𝒙 in g(𝒙).
⇒ 𝒈 𝒙 = 𝝎𝑻
𝒙𝒑 + 𝑟
𝝎𝑻𝝎
𝝎
+ 𝝎𝟎
⇒ 𝒈 𝒙 = 𝝎𝑻𝒙𝒑 + 𝝎𝟎 + 𝑟
𝝎𝑻
𝝎
𝝎
⇒ 𝒈 𝒙 = 𝑟
𝝎𝑻
𝝎
𝝎
⇒ 𝑟 =
𝑔(𝒙)
𝝎

22. Finding Separating Hyperplane with maximum Margin?
Distance of 𝒙𝒑 from g(x)=0 is
⇒ 𝑟𝟎 =
𝝎𝑇
𝟎 + 𝜔0
𝝎
𝑟 =
𝑔(𝒙)
𝝎
𝑟 =
𝑔(𝒙)
𝝎
So, the distance of origin from g(x)=0 is
⇒ 𝑟𝟎 =
𝜔0
𝝎

23. Finding Separating Hyperplane with maximum Margin?
What is the Margin between H+ and H-?

24. Finding Separating Hyperplane with maximum Margin?
To define the expression for H+ and H-, let us make the
following assumptions.
Given a datapoint < 𝒙𝒊, 𝑦𝒊> where 𝑦𝒊𝜖{+𝑣𝑒, −𝑣𝑒} is the class
label of 𝒙𝒊,
• let us replace –ve by +1, and –ve by -1.

25. Finding Separating Hyperplane with maximum Margin?
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≥ 1, ∀𝑦𝒊 = +1
To define the expression for H+ and H-, let us make the
following assumptions.
Given a datapoint < 𝒙𝒊, 𝑦𝒊> where 𝑦𝒊𝜖{+𝑣𝑒, −𝑣𝑒} is the class
label of 𝒙𝒊,
• Let us replace –ve by +1, and –ve by -1.
• Now, each data point will satisfy the following
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≤ −1, ∀𝑦𝒊 = −1

26. Finding Separating Hyperplane with maximum Margin?
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≥ 1, ∀𝑦𝒊 = +1
To define the expression for H+ and H-, let us make the
following assumptions.
Given a datapoint < 𝒙𝒊, 𝑦𝒊> where 𝑦𝒊𝜖{+𝑣𝑒, −𝑣𝑒} is the class
label of 𝒙𝒊,
• let us replace –ve by +1, and –ve by -1.
• Now, each data point will satisfy the following
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≤ −1, ∀𝑦𝒊 = −1
The above two expression can be merged to form a single expression
𝑦𝒊(𝝎𝑇
𝒙𝒊 + 𝜔𝟎) ≥ 1, ∀𝒙𝒊

27. Finding Separating Hyperplane with maximum Margin?
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≥ 1, ∀𝑦𝒊 = +1
To define the expression for H+ and H-, let us make the
following assumptions.
Given a datapoint < 𝒙𝒊, 𝑦𝒊> where 𝑦𝒊𝜖{+𝑣𝑒, −𝑣𝑒} is the class
label of 𝒙𝒊,
• let us replace –ve by +1, and –ve by -1.
• Now, each data point will satisfy the following
𝝎𝑇
𝒙𝒊 + 𝜔𝟎 ≤ −1, ∀𝑦𝒊 = −1
The above two expression can be merged to form a single expression
𝑦𝒊(𝝎𝑇
𝒙𝒊 + 𝜔𝟎) ≥ 1, ∀𝒙𝒊
𝑦𝒊(𝝎𝑇
𝒙𝒊 + 𝜔𝟎) − 1 ≥ 0, ∀𝒙𝒊

28. Finding Separating Hyperplane with maximum Margin?
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 = 1
𝒈 𝒙 = 𝝎𝑇
𝒙 + 𝜔𝟎 = −1
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 =0
H+:
H-:
H:

29. Finding Separating Hyperplane with maximum Margin?
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 = 1
𝒈 𝒙 = 𝝎𝑇
𝒙 + 𝜔𝟎 = −1
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 =0
H+:
H-:
H:
Margin = 𝑟𝑯+ − 𝑟𝑯−
=
𝜔0 − 1
𝝎
−
𝜔0 + 1
𝝎
=
𝜔0 − 1 −𝜔0 −1
𝝎
⇒ 𝑀𝑎𝑟𝑔𝑖𝑛 =
−2
𝝎

30. Finding Separating Hyperplane with maximum Margin?
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 = 1
𝒈 𝒙 = 𝝎𝑇
𝒙 + 𝜔𝟎 = −1
𝒈 𝒙 = 𝝎𝑇𝒙 + 𝜔𝟎 =0
H+:
H-:
H:
Margin = 𝑟𝑯+ − 𝑟𝑯−
=
𝜔0 − 1
𝝎
−
𝜔0 + 1
𝝎
=
𝜔0 − 1 −𝜔0 −1
𝝎
⇒ 𝑀𝑎𝑟𝑔𝑖𝑛 =
−2
𝝎
As we are interested in the absolute value, we consider the margin as
2
𝝎

31. Finding Separating Hyperplane with maximum Margin?
𝑀𝑎𝑟𝑔𝑖𝑛 =
2
𝝎
⇒ 𝑀𝑎𝑟𝑔𝑖𝑛 =
1
𝝎
2
Task is to find the hyperplane (g(x)=0) that maximizes
the margin
2
𝝎

32. Finding Separating Hyperplane with maximum Margin?
𝑀𝑎𝑟𝑔𝑖𝑛 =
2
𝝎
⇒ 𝑀𝑎𝑟𝑔𝑖𝑛 =
1
𝝎
2
Task is to find the hyperplane (g(x)=0) that maximizes
the margin
2
𝝎
Maximizing
2
𝝎
is equivalent to minimizing
𝝎
𝟐
Minimizing
𝝎
𝟐
is equivalent to minimizing
𝝎𝑻𝝎
𝟐

33. Finding Separating Hyperplane with maximum Margin?
Minimize objective function
𝝎𝑻𝝎
𝟐
Subject to the constraint 𝑦𝒊(𝝎𝑇𝒙𝒊 + 𝜔𝟎) ≥ 1, ∀𝒙𝒊
Now, we need to solve the following optimization

34. Finding Separating Hyperplane with maximum Margin?
Objective function is to minimize
𝝎𝑻𝝎
𝟐
Subject to 𝑦𝒊(𝝎𝑇
𝒙𝒊 + 𝜔𝟎) ≥ 1, ∀𝒙𝒊
𝑳𝒑 =
𝝎𝑻
𝝎
𝟐
− ෍
𝒊=𝟏
𝒏
λ𝒊 𝑦𝒊(𝝎𝑇
𝒙𝒊 + 𝜔𝟎) − 1
where λ𝒊 are Lagrange multipliers
To find the parameters 𝝎 and where 𝜔0, solve
the following optimization function

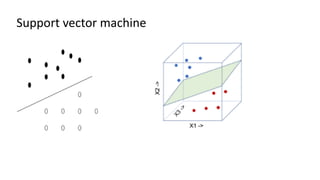
35. What are the support vectors?
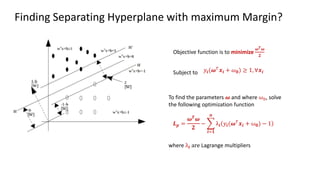
𝑳𝒑 =
𝝎𝑻
𝝎
𝟐
− ෍
𝒊=𝟏
𝒏
λ𝒊 𝑦𝒊(𝝎𝑇𝒙𝒊 + 𝜔𝟎) − 1
[
In order to find the parameters, we need to solve this objective function.
]

36. Summary
• What is separating hyperplane?
• How to define separating hyperplane?
• What are Support Vector Machine?
• How to classify a new example using SVM