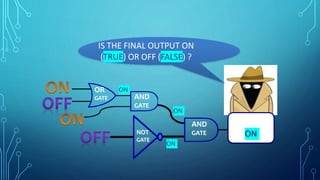
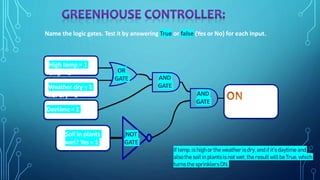
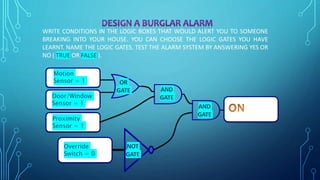
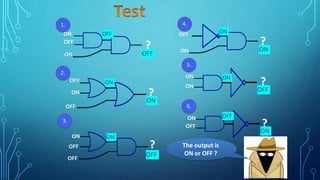
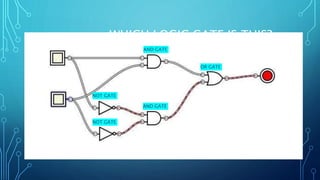
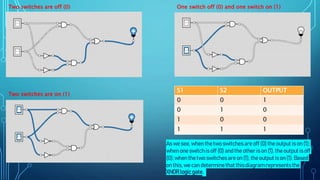
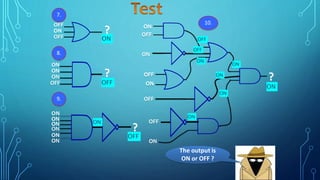
The document discusses the application of logic gates in real-life scenarios, such as controlling sprinklers and alarm systems based on various conditions. It explores the use of AND, OR, NOT, and XNOR logic gates, demonstrating how they can be tested using truth values. Additionally, it includes boolean expression simplifications and Karnaugh map methodologies for circuit analysis.

1. Logic Gates Application

2. OR
GATE AND
GATE
AND
GATE
NOT
GATE
FINAL
OUTPUT
ON ? OFF ?
IS THE FINAL OUTPUT ON
(TRUE) OR OFF (FALSE) ?
ON
ON
ON
ON

3. OR
GATE
YES,
Turn
sprinklers
on
High temp = 1
emp = 1
Weather dry = 1
her dry = 1
Daytime = 1
Soil in plants
wet? Yes = 1
Name the logic gates. Test it by answering True or false (Yes or No) for each Input.
AND
GATE
AND
GATE
NOT
GATE
If temp. is high or the weather isdry, and if it’sdaytime and
also the soil in plantsis not wet, the resultwill be True, which
turns the sprinklersON.

4. YES,
Alert
police
WRITE CONDITIONS IN THE LOGIC BOXES THAT WOULD ALERT YOU TO SOMEONE
BREAKING INTO YOUR HOUSE. YOU CAN CHOOSE THE LOGIC GATES YOU HAVE
LEARNT. NAME THE LOGIC GATES. TEST THE ALARM SYSTEM BY ANSWERING YES OR
NO ( TRUE OR FALSE ).
Motion
Sensor = 1
Door/Window
Sensor = 1
Proximity
Sensor = 1
Override
Switch = 0
OR
GATE AND
GATE
AND
GATE
NOT
GATE

5. 2.
3.
6.
5.
?
ON
ON
?
ON
4.
OFF
?
ON
OFF
?
ON
OFF
OFF
?
ON
OFF
OFF
?
ON
1.
ON
OFF
The output is
ON or OFF ?
OFF
OFF
ON
ON
ON
OFF
ON
ON
ON
ON
OFF
OFF

6. WHICH LOGIC GATE IS THIS?
AND GATE
AND GATE
NOT GATE
NOT GATE
OR GATE

7. Two switches are off (0) One switch off (0) and one switch on (1)
Two switches are on (1)
S1 S2 OUTPUT
0 0 1
0 1 0
1 0 0
1 1 1
As we see, when the two switchesare off (0) the output is on (1);
when one switchis off (0) and the other is on (1), the output is off
(0); when the two switchesare on (1), the output is on (1). Based
on this,we can determinethat thisdiagram represents the
XNORlogicgate.

8. ?
8.
9.
10.
ON
ON
ON
?
ON
ON
ON
ON
ON
ON
?
ON
ON
ON
OFF
OFF
ON
OFF
OFF
?
7.
OFF
ON
OFF
OFF
The output is
ON or OFF ?
OFF
OFF
ON
ON
OFF
OFF
ON
ON
ON
ON
ON
ON

9. Obtain the simplified
Boolean expressions for
output variables F, G, and H
in terms of input
variables in the circuit
shown.
For simplification use
Boolean rules and Karnaugh
maps (SOP or POS as you
wish).

10. X3 = (A3’B3 + A3B3’)’ = (A3’B3)’ (A3B3’)’ = (A3+B3’) (A3’+B3) = A3A3’+A3B3+A3’B3’+B3B3’ = A3B3+A3’B3’ =
A3+A3’B3’ = A3+B3’
X2 = (A2’B2 + A2B2’)’ = (A2’B2)’ (A2B2’)’ = (A2+B2’) (A2’+B2) = A2A2’+A2B2+A2’B2’+B2B2’ = A2B2+A2’B2’ =
A2+A2’B2’ = A2+B2’
X1 = (A1’B1 + A1B1’)’ = (A1’B1)’ (A1B1’)’ = (A1+B1’) (A1’+B1) = A1A1’+A1B1+A1’B1’+B1B1’ = A1B1+A1’B1’ =
A1+A1’B1’ = A1+B1’
X0 = (A0’B0 + A0B0’)’ = (A0’B0)’ (A0B0’)’ = (A0+B0’) (A0’+B0) = A0A0’+A0B0+A0’B0’+B0B0’ = A0B0+A0’B0’ =
A0+A0’B0’ = A0+B0’
H = X3 * X2 * X1 * X0 = (A3+B3’) (A2+B2’) (A1+B1’) (A0+B0’)
Z3 = X3 (A2’B2) = A2’B2 (A3+B3’)
Z2 = X3 X2 (A1’B1) = A1’B1 (A3+B3’)(A2+B2’)
Z1 = X3 X2 X1 (A0’B0) = A0’B0 (A3+B3’)(A2+B2’)(A1+B1’)
F = A3’B3 + Z3 + Z2 + Z1
F = A3’B3+A2’B2 (A3+B3’)+A1’B1 (A3+B3’)(A2+B2’)+A0’B0 (A3+B3’)(A2+B2’)(A1+B1’)
F = A3’B3+(A2’B2+A3’B3)A3 Factor out A3+B3’ from the first two terms
F = A3’B3+A2’B2A3+A3’B3A3 Distribute A3 through the second term
F = A3’B3+A2’B2A3+A3’B3 Simplify A3’B3A3 to A3’B3 since A3*A3=A3
F = A3’B3+A2’B2A3+ (A1’B1 (A2+B2’)+A0’B0 (A2+B2’)(A1+B1’)) (A3+B3’) Factor out A3+B3’ from the last two terms
F = A3’B3+A2’B2A3+ A1’B1 (A2+B2’)A3 +A0’B0(A2+B2’)(A1+B1’)A3 +A1’B1(A2+B2’)B3’ +A0’B0 (A2+B2’)(A1+B1’)B3’
Distribute A3+B3’ through the last two terms

11. Y3 = X3 (A2B2’) = A2B2’(A3+B3’)
Y2 = X2 X3 (A1B1’) = A1B1’ (A3+B3’) (A2+B2’)
Y1 = X1 X2 X3 (A0B0’) = A0B0’ (A3+B3’) (A2+B2’) (A1+B1’)
G = A3B3’ + Y3 + Y2 + Y1
G = A3B3’+ A2B2’(A3+B3’)+ A1B1’ (A3+B3’) (A2+B2’)+ A0B0’ (A3+B3’) (A2+B2’) (A1+B1’)
G = A3B3’+ A2B2’A3+ A2B2’B3’+ A1B1’A3A2+ A1B1’B3’A2+ A0B0’A3A2A1+ A0B0’B3’A2A1+ A0B0’A3A2B1’B3’
Distributing
G = A3(B3’+ A2B2’+ A1B1’A2B1’B3’)+ A2(A3+ B3’+ A1B1’B3’+ A0B0’A1B1’B3’) Grouping terms with A3 and A2
G = A3(B3’+ A2B2’+ A1B1’A2B1’B3’)+ A2(A3+ B3’+ A1B1’B3’(1+ A0B0’A1)) Factoring out A1B1’B3’ from the third term
G = A3(B3’+ A2B2’+ A1B1’A2B1’B3’)+ A2(A3+ B3’+ A1B1’B3’) Since 1+ A0B0’A1 = 1, simplify the third term
G = B3’(A3+ A1B1’A2)+ A2(A3+ B3’+ A1B1’B3’)+ A3B2’B1’ Simplify the expression by factoring out common terms
G = B3’(A3+ A1B1’A2)+ A2(A3+ B3’+ A1B1’B3’)+ A3B2’B1’