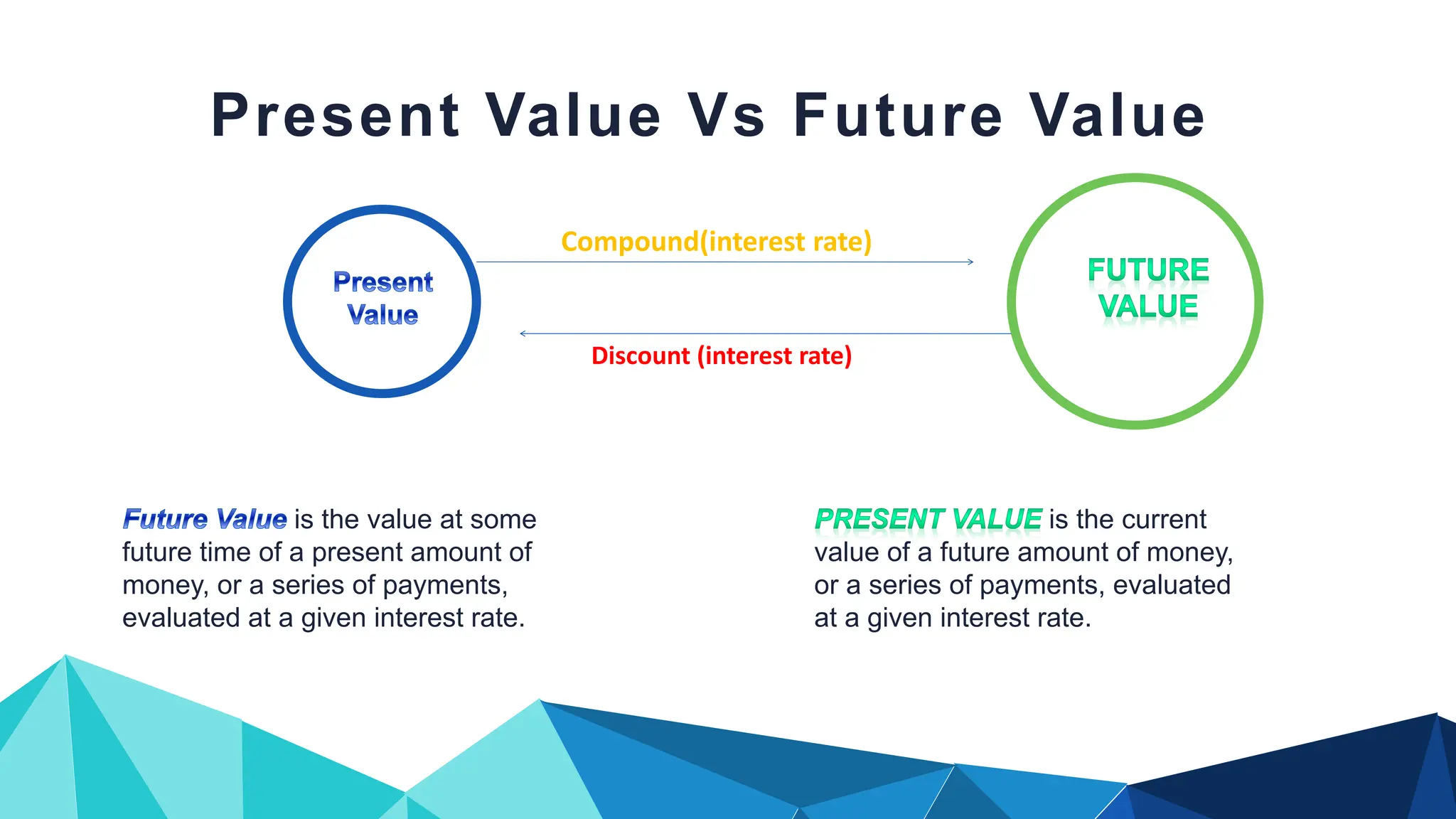
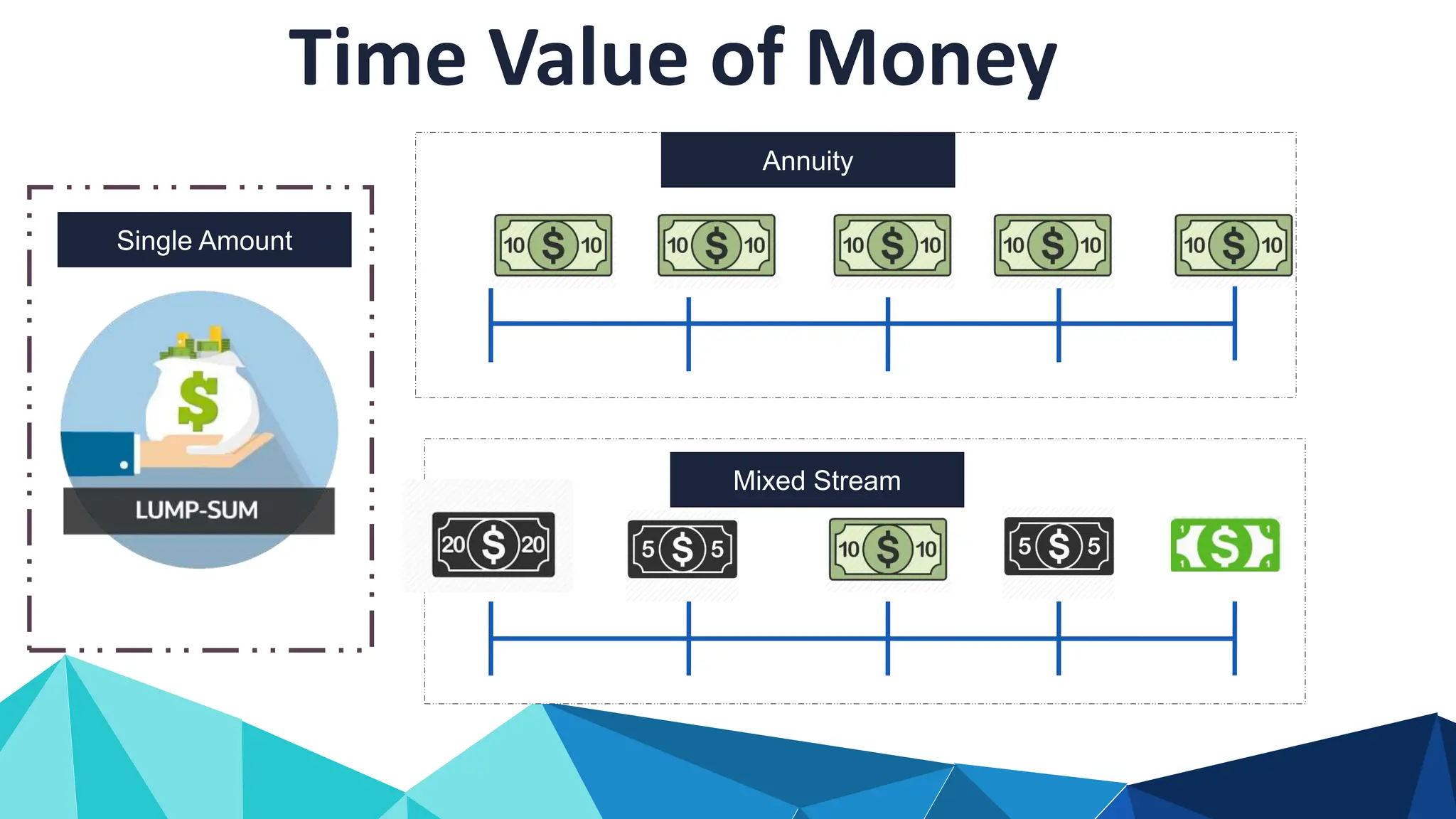
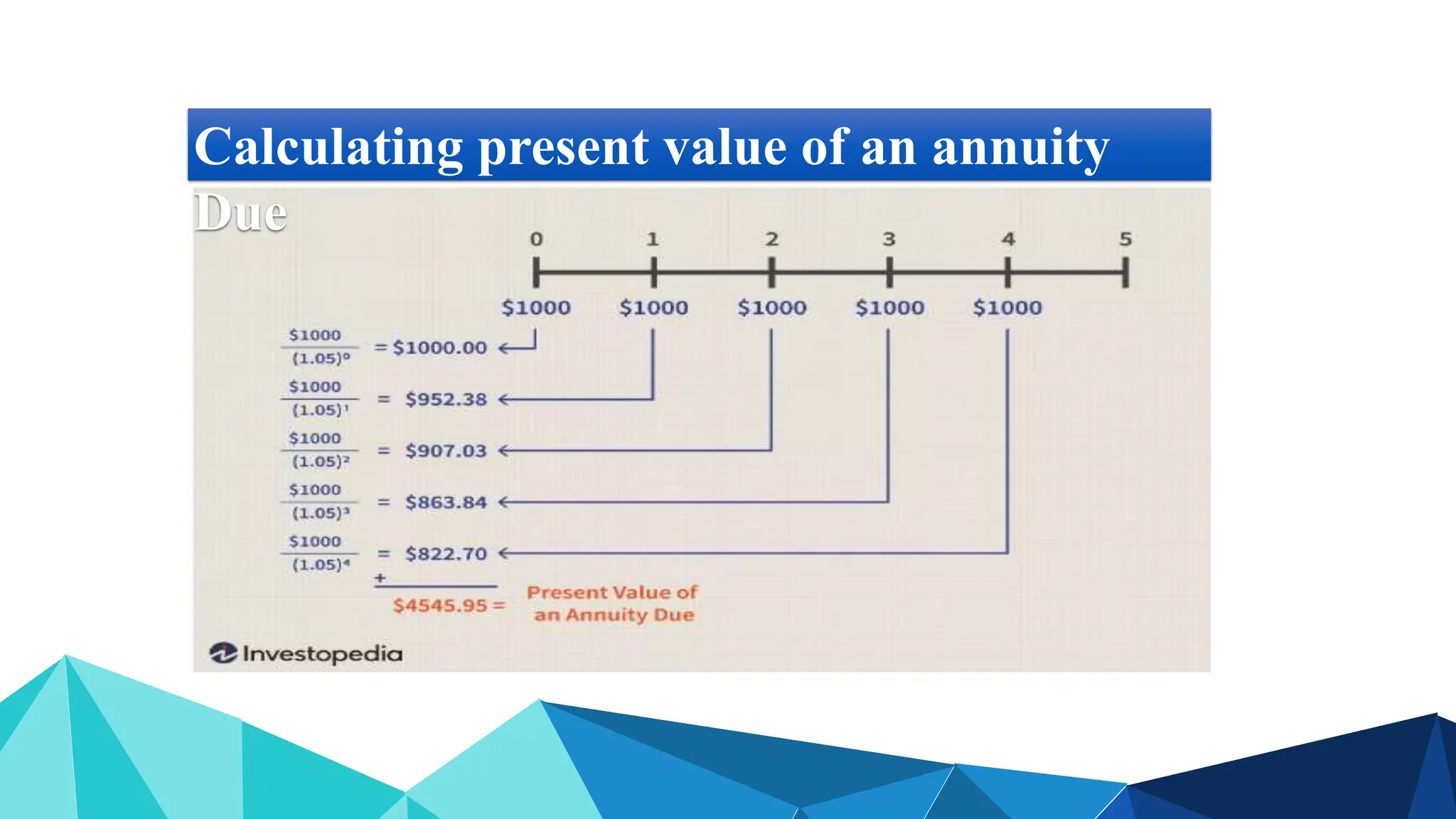
The document explains the time value of money, detailing concepts like simple and compound interest, present and future values, and their calculations. It covers various financial formulas and scenarios, including annuities and mixed cash flows, highlighting the importance of interest rates and compounding frequency. Practical examples and exercises illustrate these concepts to aid understanding.

1. Time Value of Money
Prepared By: Haseeb Yaqoob
Lecturer
Faculty of Department
of Mechanical

2. Interest Rate
• Simple Interest Rate
• Compound Interest Rate
Future Value (single amount ,annuity, mixed Stream)
Present Value
Annuity
• Ordinary Annuity
• Annuity Due
The Rule of 72
Compounding Periods
Amortization of Loan

3. Obviously, $10,000 today.
You already recognize that there is TIME
VALUE TO MONEY!!
This concept emerged because money
has the capacity to earn.
Which would you prefer – $10,000
today or $10,000 in 5 years?

4. Why Time?
Why is TIME such an important
element in your decision?
TIME allows you the opportunity to postpone consumption
and earn INTEREST.

5. Interest on Interest is simply known as
compound Interest.
Or
Interest paid (earned) on any previous
interest earned, as well as on the
principal borrowed (lent).
Compound Interest = P.V × (1+i)n
Interest paid (earned) on only the
original amount, or principal, borrowed
(lent).
Formula:
Simple Interest = P.V × i × n
Simple Interest Vs Compound Interest
Where as:
P.V = Present Value (at time 0)
i = Interest Rate
n = Number of Years

6. Formula Derivation for Simple Interest
Year Simple
Interest
Total Amount Total Amount
1 (after 1 year) I1= P×i T1 = P+ (P×i)
2 (after 2 years) I2= P×i T2 =P+(P×i)+(P×i) =P+2Pi =P(1+2i)
3 (after 3 years) I3= P×i T3 =P+(P×i)+(P×i)+(P×i) =P+3Pi =P(1+3i)
4 (after 4 years) I4= P×i T4 =P+(P×i)+(P×i)+(P×i)+(P×i) =P+4Pi =P(1+4i)
5 (after 5 years) I5= P×i T5 =P +(P×i)+(P×i)+(P×i)+(P×i)+(P×i) =P+5Pi =P(1+5i)
Formula
Derivation
In= P×i×n
Tn= P ×(1+ni)

7. Year Compound
Interest
Total Amount Total Amount
1 (after 1 year) I1= (P×i) T1 = P+ (P×i) =P(1+i) =P(1+i)
2 (after 2 years) I2= (P×i)×i T2 =P(1+i)+P(1+i)×i =P(1+i) [1+i] =P(1+i)2
3 (after 3 years) I3= (P×i)2×i T3 =P(1+i)2 + P(1+i)2 ×i =P(1+i)2[1+i] =P(1+i)3
4 (after 4 years) I4= (P×i)3×i T4 =P(1+i)3 +P(1+i)3 × i =P(1+i)3 [1+i] =P(1+i)4
5 (after 5 years) I5= (P×i)4×i T5 =P(1+i)4 +P(1+i)4 ×i =P(1+i)4 [1+i] =P(1+i)5
Formula
Derivation
Tn= P ×(1+i)n
Formula Derivation for Compound Interest

8. Question
Calculate the total amount
by using simple interest and
Compound interest for Rs.
100 deposit today, at 8% rate
of interest for 5- years.
Here we have:
P.V = 100 Rs
i = 8%
n = 5 Years
Years Simple Interest Total Amount
1 100×0.08= 8 100+8=108
2 100×0.08= 8 108+8=116
3 100×0.08= 8 116+8= 124
4 100×0.08= 8 124+8=132
5 100×0.08= 8 132+8=140
years Compound Interest Total Amount
1 100×0.08= 8 100+8=108
2 108×0.08=8.64 108+8.64=116.64
3 116.64×0.08=9.33 116.64+9.33=125.97
4 125.97×0.08=10.08 125.97+10.08=136.05
5 136.05×0.08=10.85 136.05+10.85=146.63

10. Present Value Vs Future Value
Compound(interest rate)
Discount (interest rate)
is the value at some
future time of a present amount of
money, or a series of payments,
evaluated at a given interest rate.
is the current
value of a future amount of money,
or a series of payments, evaluated
at a given interest rate.

11. There are four ways to find the Present and Future
values (single amount, annuity, mixed stream)
1. By using formula
2. By using the interest factor table values
3. By using financial calculator
4. By using excel sheet

12. Time Value of Money
Annuity
Mixed Stream
Single Amount

14. F.V= Future Value
P.V= Present Value
n = Number of years
i= Interest rate
FVIF= Future value interest factor

15. Consider Mr. Ali deposits $100 into a savings account. If the interest rate is 8 percent, compounded
annually, how much will the $100 be worth at the end of 4 years?
136
100×(1+0.08)4

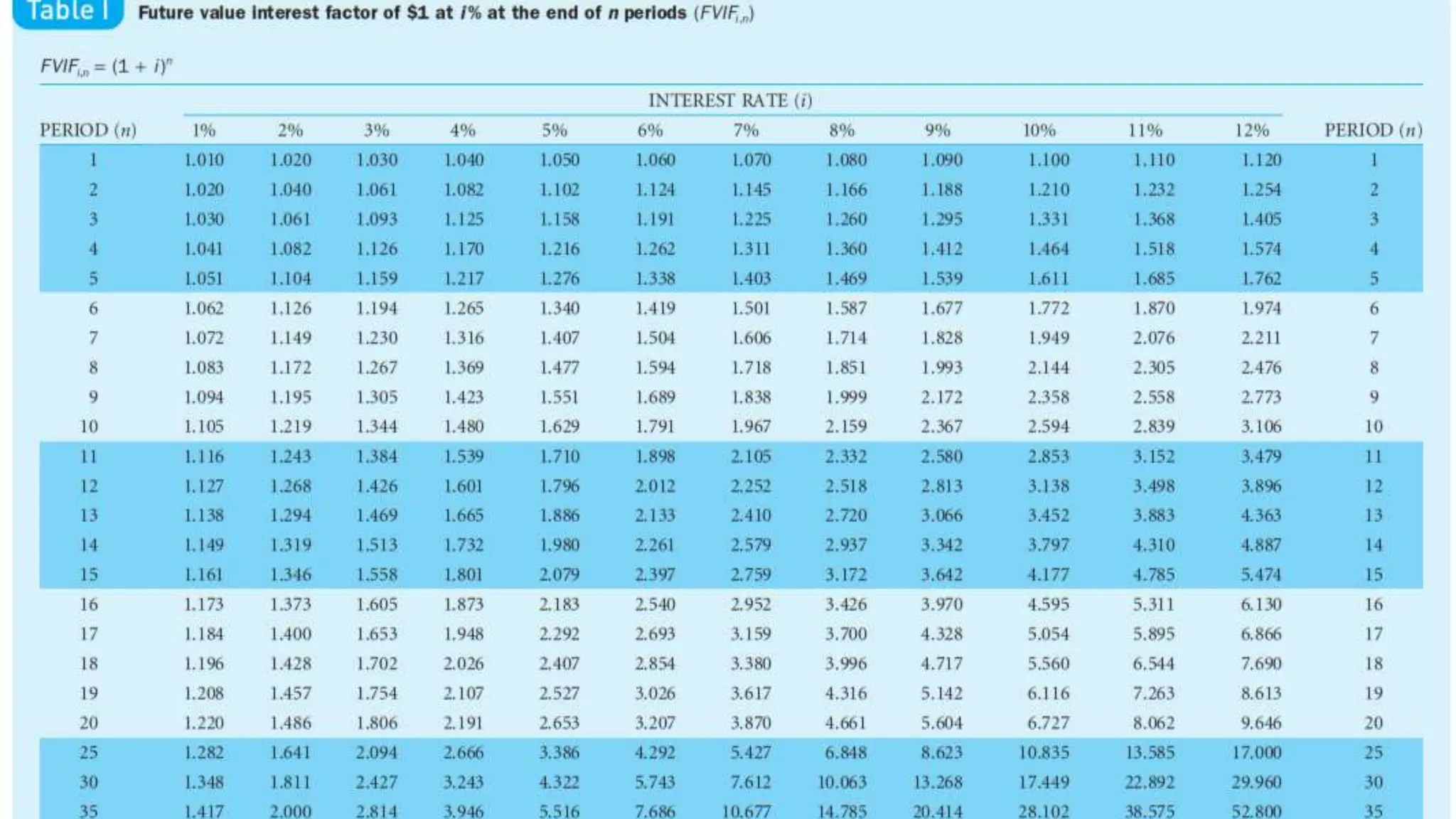
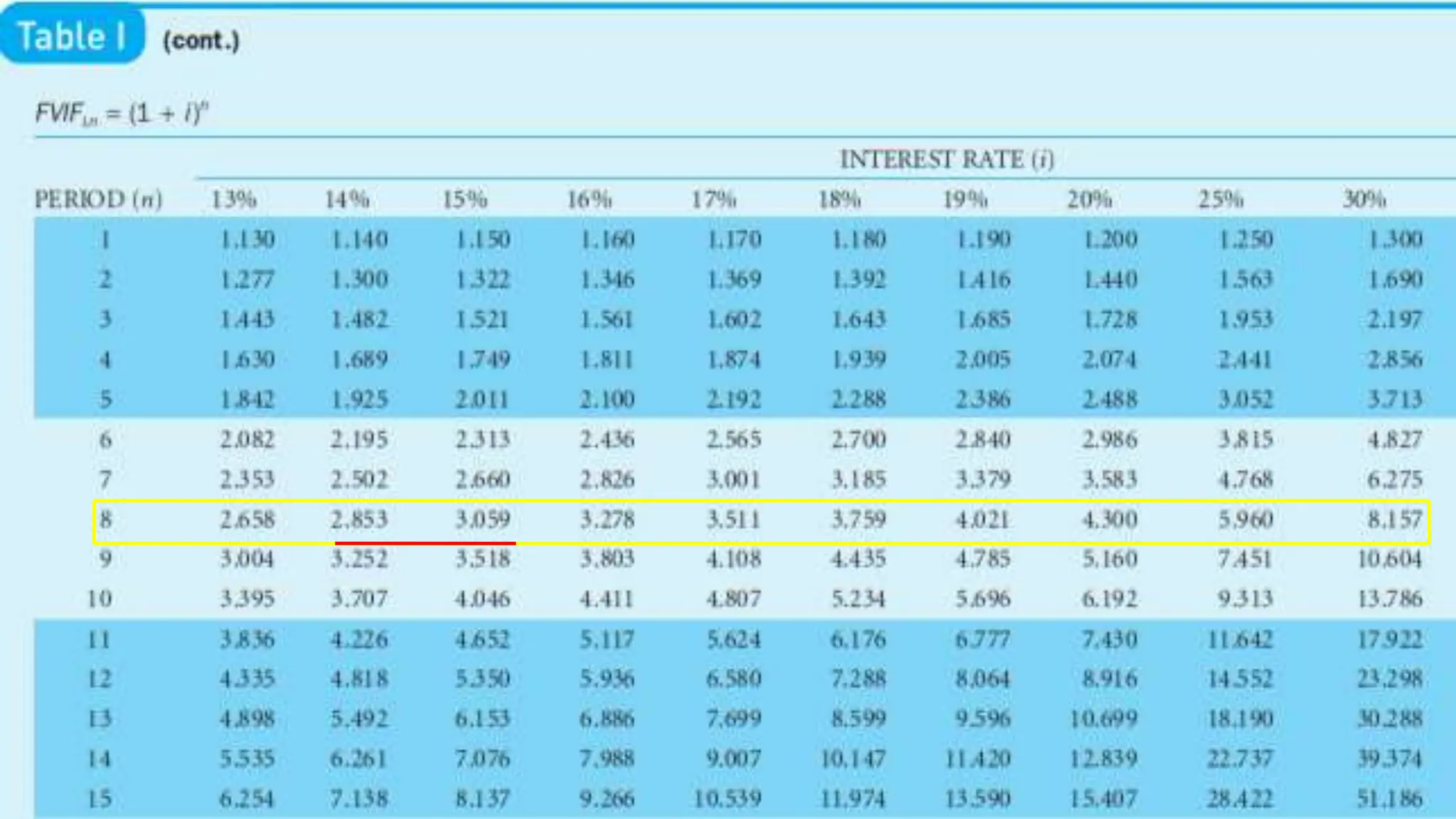
16. Using Table 1: Future Value Interest Factor( FVIF i%,n)
FV4 = $1,00(FVIF8%,4)
= $1,00 (1.360)
= $136 [Due to Rounding]
FVn= PV × FVIF i%,n

19. F.V= Future Value
P.V= Present Value
n = Number of years
i= Interest rate
PVIF= Present value interest factor

20. what amount Mr.Ali should invest now in order to get $136 after 4 years provided that interest rate is 8% a
savings account. If the interest rate is 8 percent.
136
?
$100

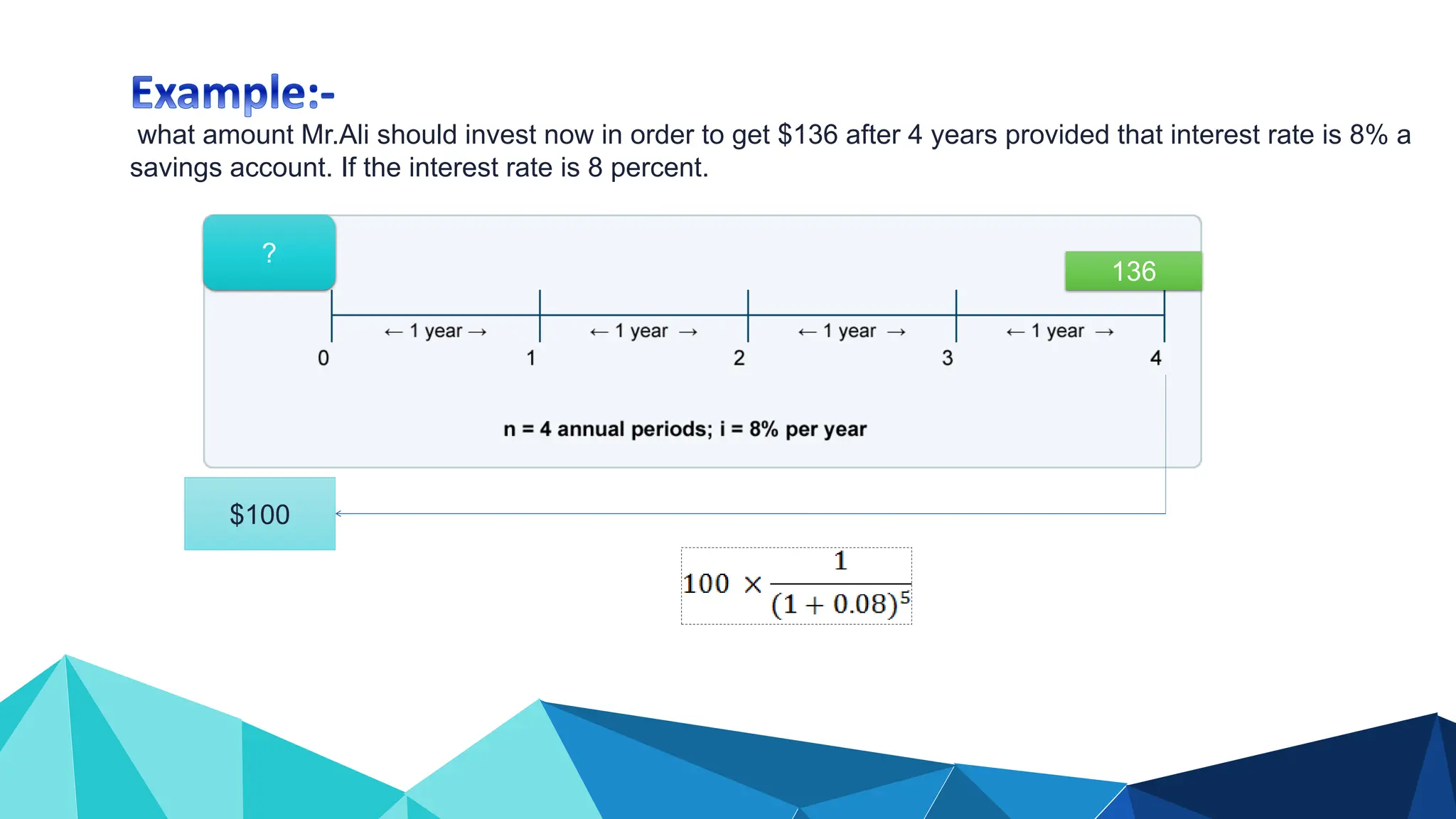
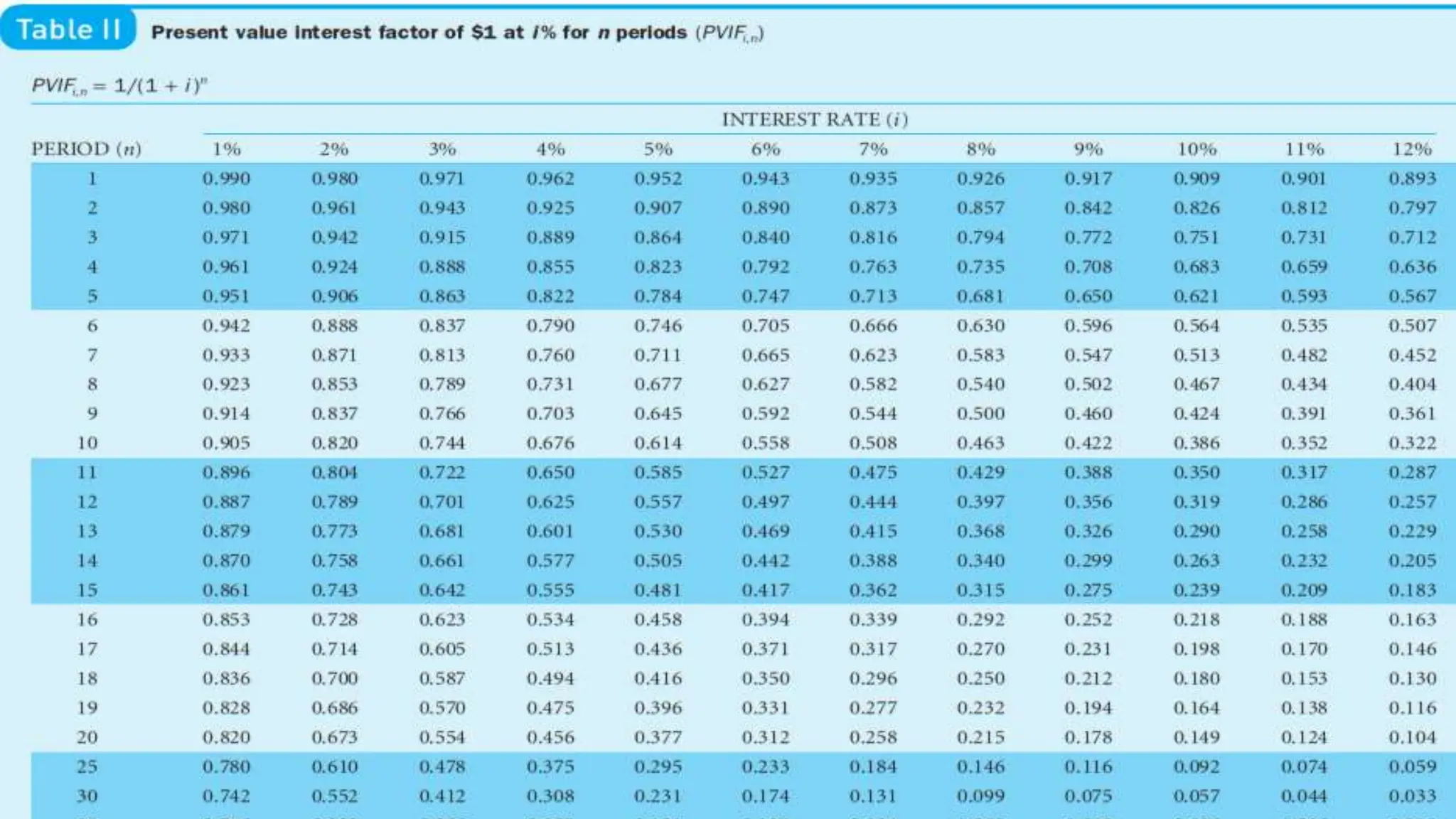
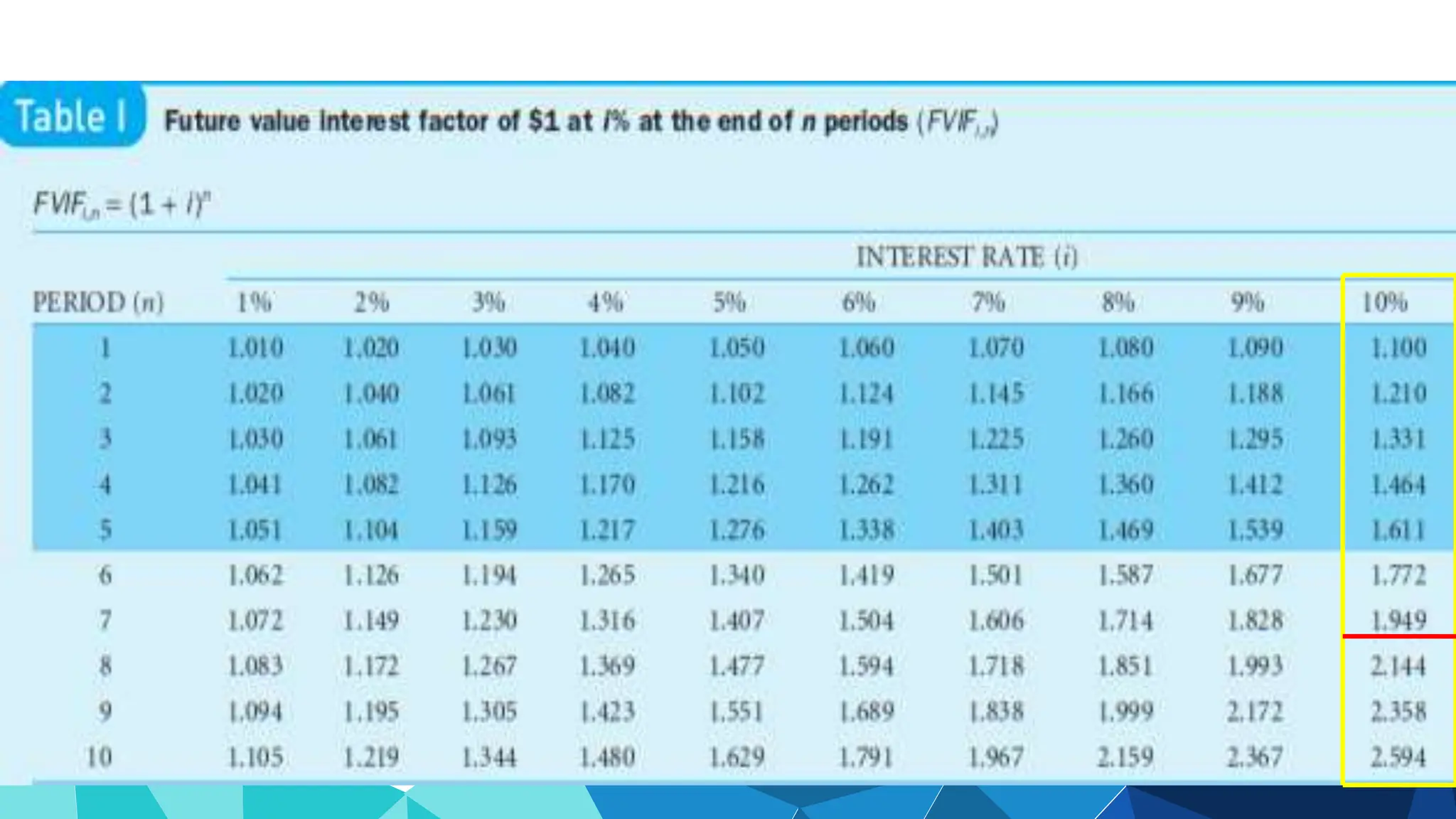
21. Using Table II: Present Value Interest Factor( PVIF i%,n)
PV4 = $136(PVIF8%,4)
= $136(0.735)
= $99.9 $100 [Due to Rounding]
PVn= FV ×PVIF i%,n

23. Sometimes we face with a time-value-of money situation in which,
Future Value=FV= known
Present Value=PV= known,
Number of time periods=n=known
Compound Interest Rate=i=?
Such Interest rate can be found;
By using reverse table approach
By Taking reciprocal power to eliminate it
Unknown Interest (or Discount) Rate

24. Let’s assume that, if you invest $1,000 today, you will receive $3,000 in exactly after 8 years. The
compound interest (or discount) rate implicit in this situation can be found by rearranging either a
basic future value or present value equation.
Reading across the 8-period row in Table I. we look for the future value interest factor (FVIF) that
comes closest to our calculated value of 3. In our table, that interest factor is 3.059 and is found in the
15% column. Because 3.059 is slightly larger than 3.
we conclude that the interest rate implicit in the example situation is actually slightly less than 15%.
By using reverse table approach

26. 3000=1000 (1+i)8
1.1472 = 1+i
1.1472-1 = i
0.1472 =i
Or 14% = i
3= (1+i)8
By Taking reciprocal power to eliminate it

27. Unknown Number of Compounding (or Discounting) Periods
At times we may need to know how long it will take for a dollar amount invested today to grow
to a certain future value given a particular compound rate of interest.
For example, how long would it take for an invest$1,000 to grow to $1,900 if we invested it at a
compound annual interest rate of 10 percent?
Future Value=FV= known
Present Value=PV= known,
Compound Interest Rate=i=known
Number of time periods=n=?
The unknown period can be found;
By using reverse table approach
By using logarithm power rule

28. Reading down the 10% column in Table I. we look for the future value interest factor (FVIF) in that column
that is closest to our calculated value. We can find that 1.949 comes closest to 1.9, and that this number
corresponds to the 7 period row.
Because 1.949 is a little larger than 1.9, we conclude that there are slightly less than 7 annual compounding
periods implicit in the example situation.
By using reverse table approach

30. By using logarithm power rule
By taking log on both sides,

31. Class Practice Questions

32. Q1:

33. Q2: Hamid wishes to find the future value of $1,700 that will be received 8
years from now. Hamid’s opportunity cost is 8%.
Q3: What single investment made today, earning 12% annual interest, will be
worth $6,000 at the end of 6 years?
Q4: You can deposit $10,000 into an account paying 9% annual interest either
today or exactly 10 years from today. How much better off will you be at the end
of 40 years if you decide to make the initial deposit today rather than 10 years
from today?

34. Q5: Misty need to have $15,000 at the end of 5 years in order to fulfill her goal of purchasing a
small sailboat. She is willing to invest the funds as a single amount today but wonders what sort
of investment return she will need to earn. Figure out the approximate annually compounded rate
of return needed in each of these cases:
a. Misty can invest $10,200 today.
b. Misty can invest $8,150 today.
c. Misty can invest $7,150 today.

35. Thanks!
You can find me at: haseeb.Yaqoob@kfueit.edu.pk
Any questions?

36. Time Value of Money
Prepared By: Haseeb Yaqoob
Lecturer
Faculty of Department
of Mechanical
Lecture 2

37. Annuity

38. • Student Loan Payments
• Car Loan Payments
• Insurance Premiums
• Mortgage Payments
• Retirement Savings
Examples of Annuities

39. Types of Annuities
An Annuity represents a series of equal payments (or
receipts) occurring over a specified number of
equidistant periods.
Ordinary Annuity : Payments or receipts occur at
the end of each period.
Annuity Due : Payments or receipts occur at the
beginning of each period.

40. 0 1 2 3 4
0 1 2 3 4
PMT PMT PMT PMT PMT
PMT PMT PMT PMT PMT
Ordinary
Annuity
Annuity
Due
i%
i%
Difference Between Ordinary annuity and Annuity Due

41. Ordinary Annuity-Annuity Due
Future Value
By using Formula
By Using Table

42. Ordinary Annuity
Future Value
By using Formula
By Using Table

43. Ordinary Annuity

44. Calculating Future Value of Ordinary
Annuity

45. Formula to calculate Future value of an Ordinary
Annuity

46. Future Value of an Ordinary Annuity by using
formula
R
R

47. Future Value Ordinary Annuity by Using Table
III
FVA5 = R (FVIFAi%,n)
FVA5 = $1,000 (FVIFA5%,5)
= $1,000 (5.526)
= $5,526

49. Annuity Due

50. Calculating Future Value of an Annuity Due

51. Formulas to calculate Future Value of an
Annuity Due

52. Calculating Future value of annuity Due by using formula

53. Future value of annuity Due Using Table III
FVADn = R (FVIFAi%,n)(1 + i)
FVAD5 = $1,000 (FVIFA5%,5)(1+0.05)
= $1,000 (5.526)(1.05)
= $5,802

55. Ordinary Annuity- Annuity Due
Present Value
By using Formula
By Using Table

56. Calculating Present Value of an ordinary
annuity

57. Formula to calculate Present Value of Ordinary
Annuity

58. Example

59. Present Value of Ordinary Annuity by Using
Table IV
PVAn = R (PVIFAi%,n)
PVA5 = $1,000 (PVIFA5%,5)
= $1,000 (4.329)
= $4,329

61. Calculating present value of an annuity
Due

62. Formulas to calculate Present Value of Annuity
Due

63. Example

64. Present Value of Annuity Due by Using Table
IV
PVADn = R (PVIFAi%,n)(1 + i)
PVAD5 = $1,000 (PVIFA5%,5)(1+0.05)
= $1,000 (4.329)(1.05)
=4,545

66. Mixed Stream
Present Value-Future Value

67. Steps to Solve Time Value of Money
Problems
1. Read problem thoroughly
2. Create a time line
3. Put cash flows and arrows on time line
4. Determine if it is a PV or FV problem
5. Determine if solution involves a single Cash Flow, annuity stream(s),
or mixed flow
6. Solve the problem
7. Check with financial calculator (optional)

68. Mixed stream Flows Example
Julie Miller will receive the set of cash flows below. What is
the Present Value at a discount rate of 10%.
0 1 2 3 4 5
10%
$600 $600 $400 $400 $100
PV0

71. 1. Solve a “piece-at-a-time” by
discounting each piece back to t=0.
2. Solve a “group-at-a-time” by first
breaking problem into groups of annuity
streams and any single cash flow groups.
Then discount each group back to t=0.
How to Solve?

72. 0 1 2 3 4 5
$600 $600 $400 $400 $100
10%
$545.45
$495.87
$300.53
$273.21
$ 62.09
$1677.15 = PV0 of the Mixed Flow
“Piece-At-A-Time”

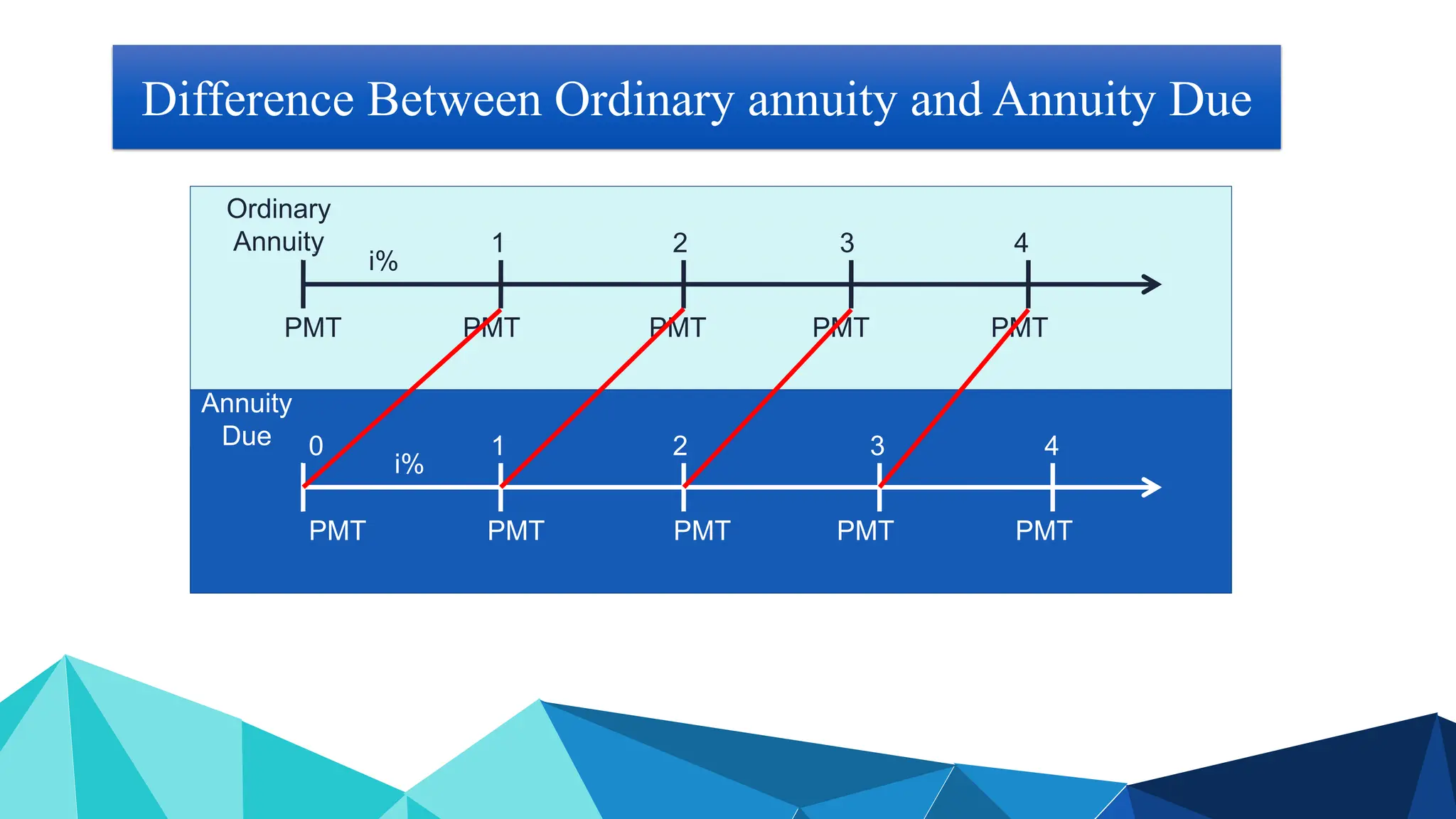
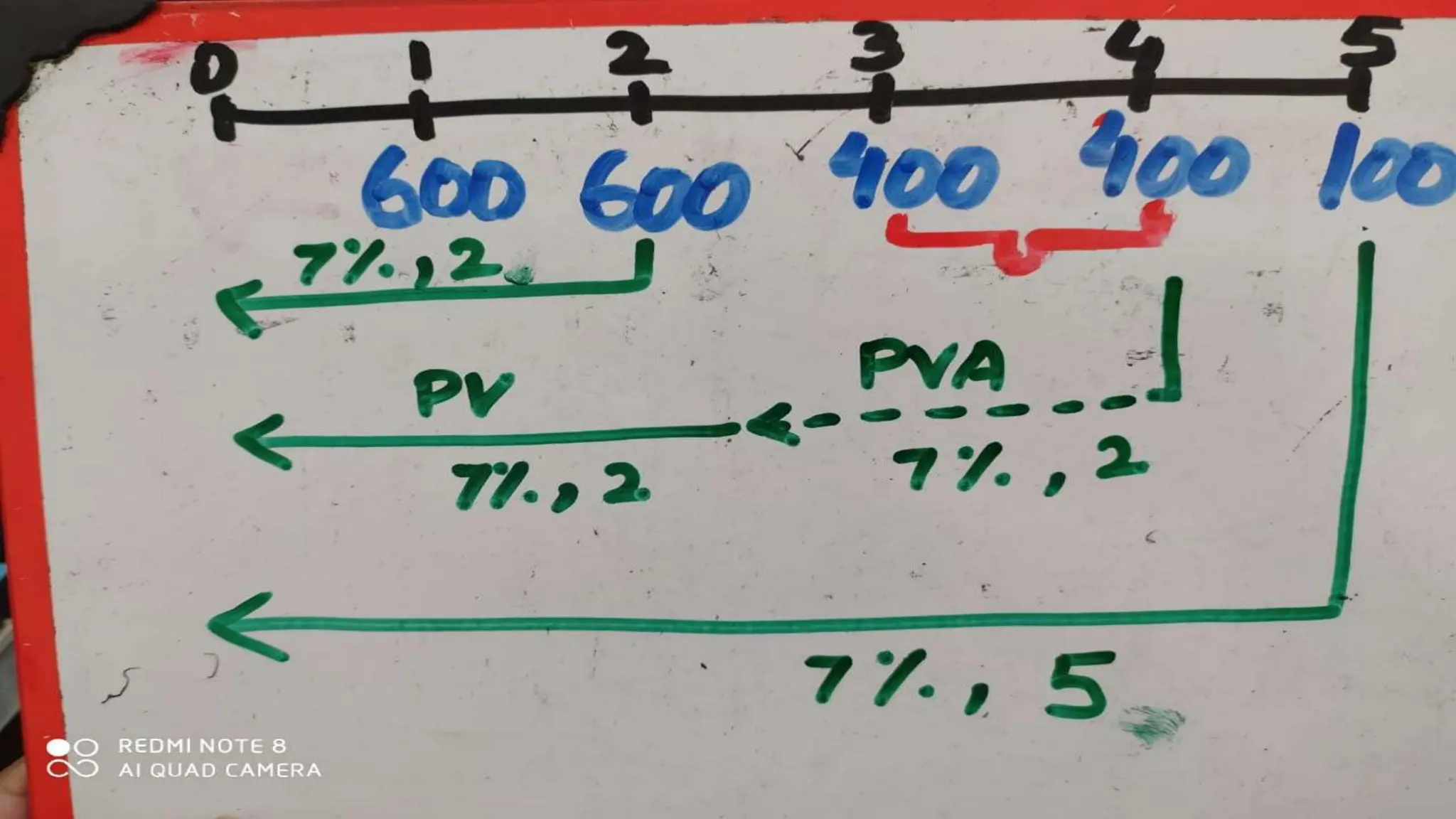
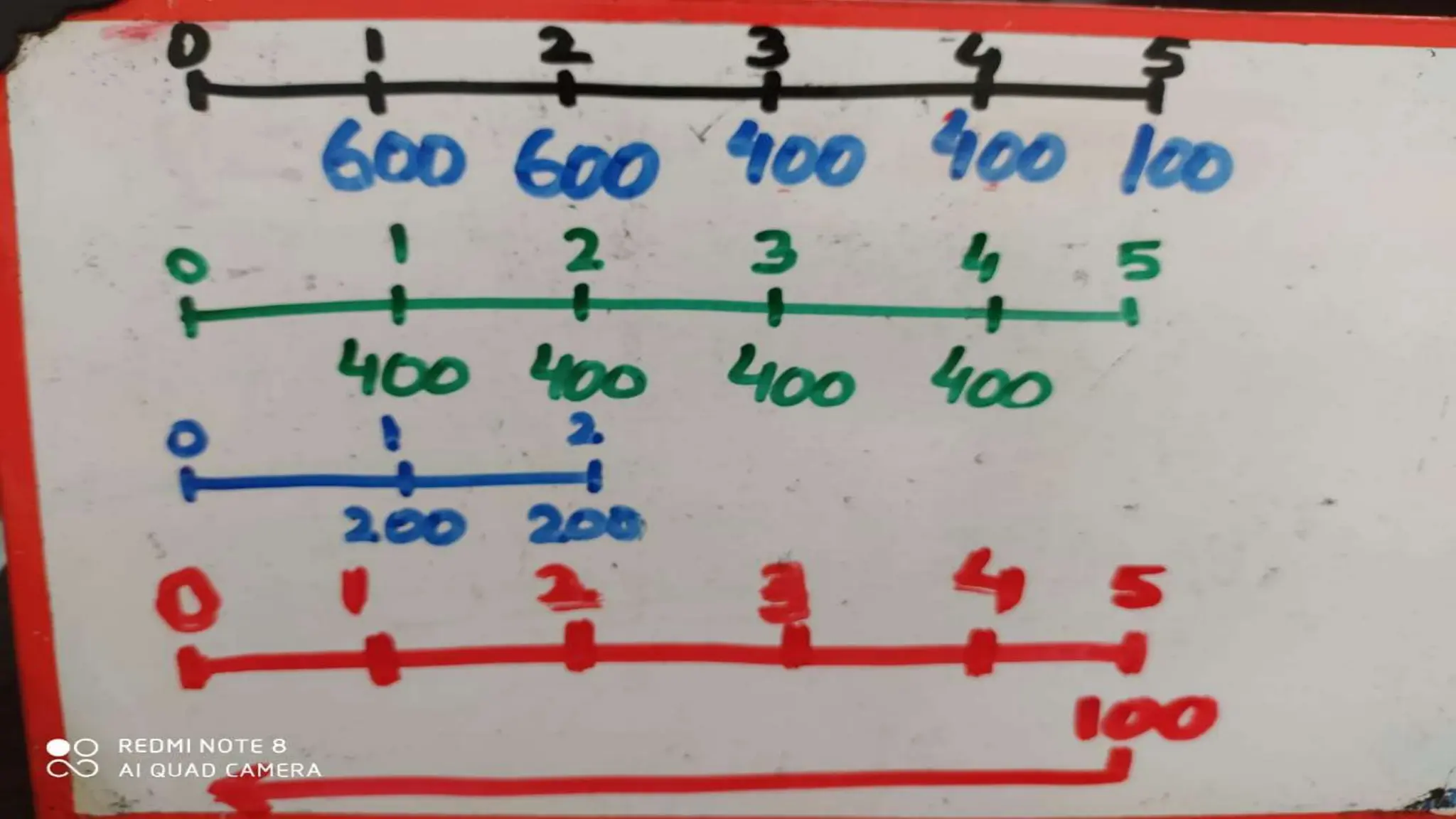
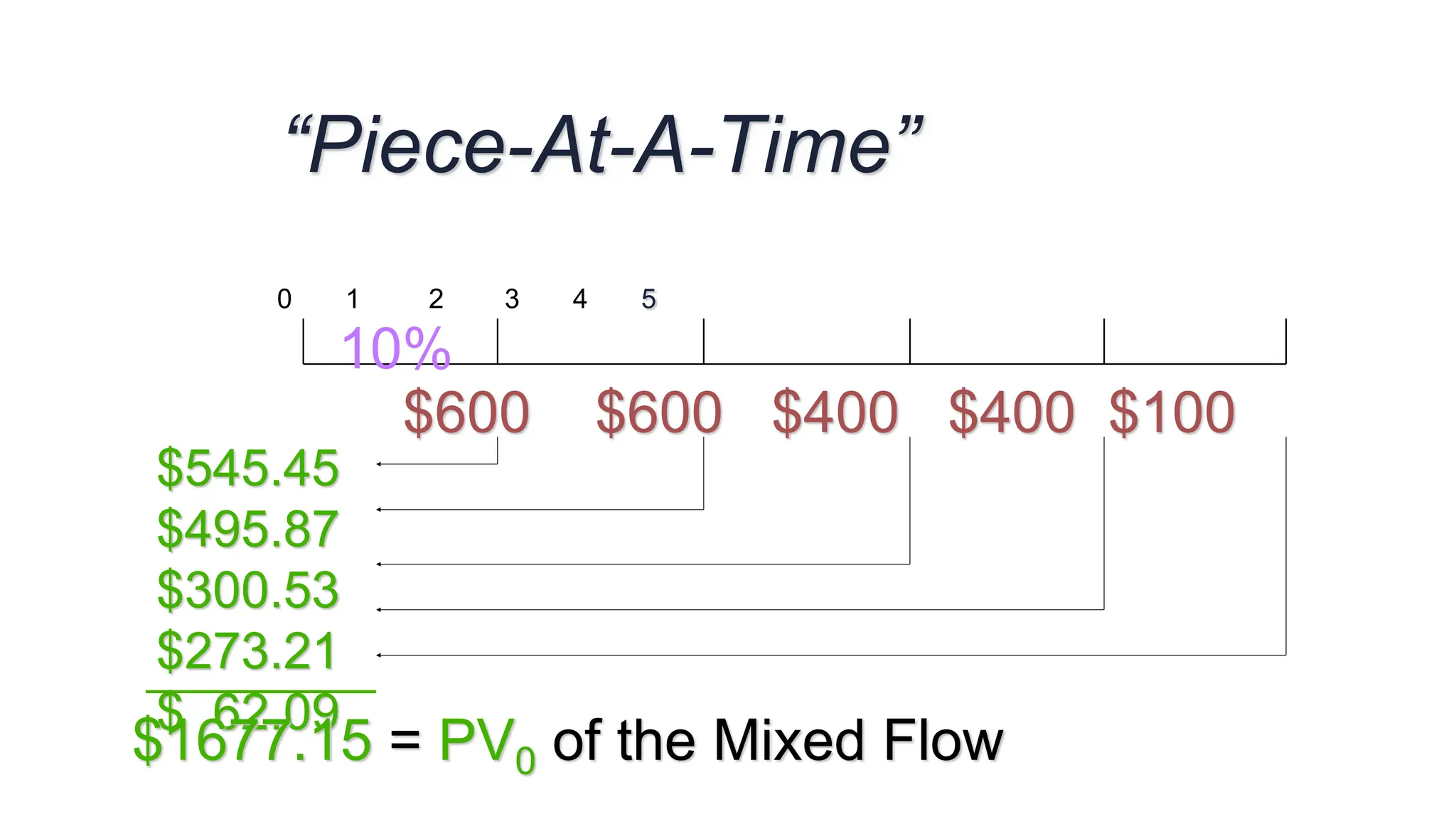
73. 0 1 2 3 4 5
$600 $600 $400 $400 $100
10%
$1,041.60
$ 573.57
$ 62.10
$1,677.27 = PV0 of Mixed Flow [Using Tables]
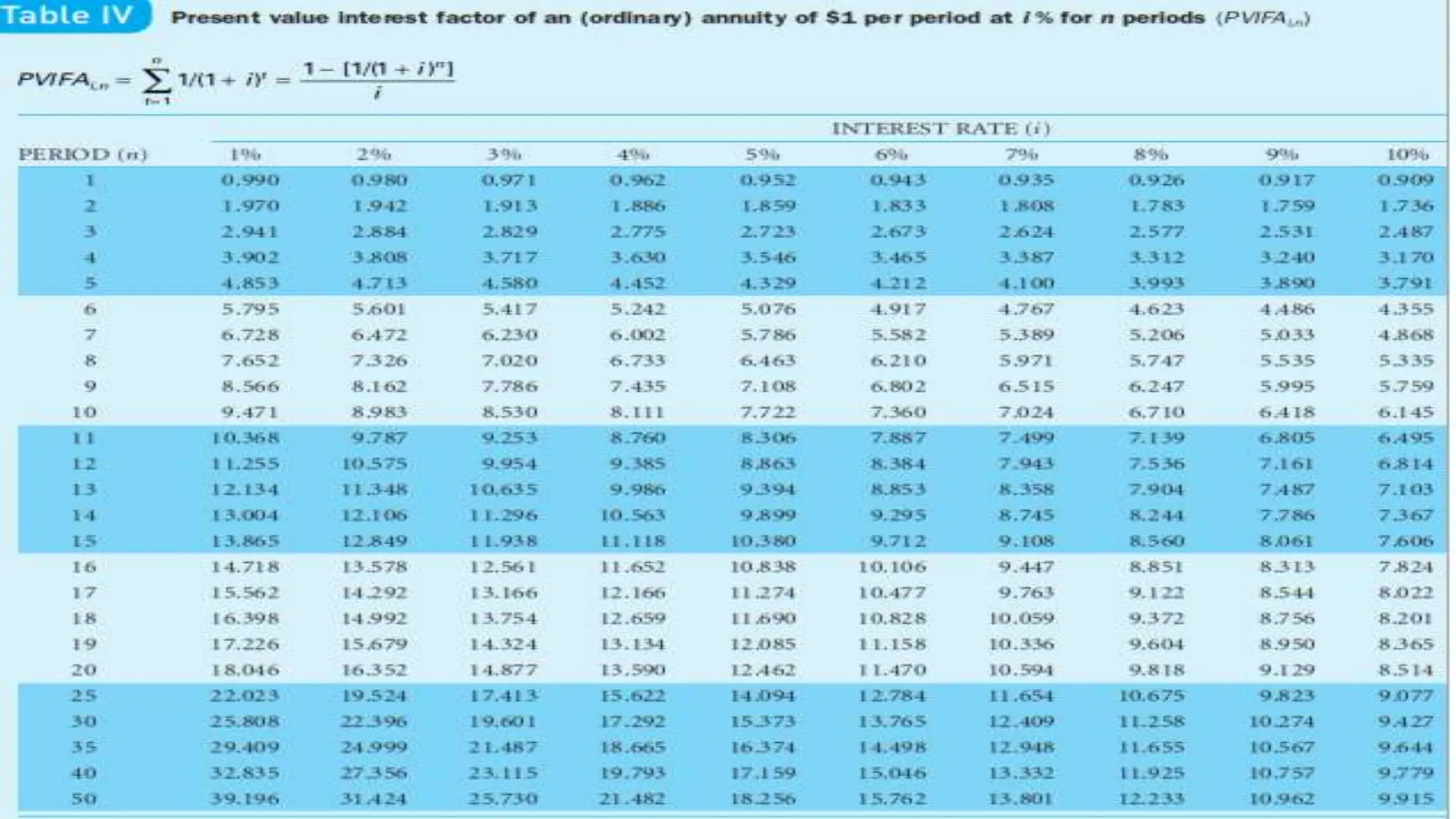
$600(PVIFA10%,2) = $600(1.736) = $1,041.60
$400(PVIFA10%,2)(PVIF10%,2) = $400(1.736)(0.826) = $573.57
$100 (PVIF10%,5) = $100 (0.621) = $62.10
“Group-At-A-Time” (#1)

74. 0 1 2 3 4
$400 $400 $400 $400
PV0 equals
$1677.30.
0 1 2
$200 $200
0 1 2 3 4 5
$100
$1,268.00
$347.20
$62.10
Plus
Plus
“Group-At-A-Time” (#2)

75. General Formula:
FVn = PV0(1 + [i/m])mn
n: Number of Years
m: Compounding Periods per Year
i: Annual Interest Rate
FVn,m: FV at the end of Year n
PV0: PV of the Cash Flow today
Frequency of Compounding

76. Julie Miller has $1,000 to invest for 2 Years at an
annual interest rate of 12%.
Annual FV2 = 1,000(1 + [0.12/1])(1)(2)
= 1,254.40
Semi FV2 = 1,000(1 + [0.12/2])(2)(2)
= 1,262.48
Impact of Frequency

77. Qrtly FV2 = 1,000(1 + [0.12/4])(4)(2)
= 1,266.77
Monthly FV2 = 1,000(1 + [0.12/12])(12)(2)
= 1,269.73
Daily FV2 = 1,000(1 + [0.12/365])(365)(2)
= 1,271.20
Impact of Frequency

78. Effective Annual Interest Rate
The actual rate of interest earned (paid) after
adjusting the nominal rate for factors such as
the number of compounding periods per year.
(1 + [ i / m ] )m – 1
Effective Annual
Interest Rate

79. Basket Wonders (BW) has a $1,000 CD at the
bank. The interest rate is 6% compounded
quarterly for 1 year. What is the Effective
Annual Interest Rate (EAR)?
EAR = ( 1 + 0.06 / 4 )4 – 1 =
1.0614 - 1 = 0.0614 or 6.14%!
BWs Effective
Annual Interest Rate

80. 1. Calculate the payment per period.
2. Determine the interest in Period t.
(Loan Balance at t – 1) x (i% / m)
3. Compute principal payment in Period t.
(Payment - Interest from Step 2)
4. Determine ending balance in Period t.
(Balance - principal payment from Step 3)
5. Start again at Step 2 and repeat.
Steps to Amortizing a Loan

81. Julie Miller is borrowing $10,000 at a compound
annual interest rate of 12%. Amortize the loan if
annual payments are made for 5 years.
Step 1: Payment
PV0 = R (PVIFA i%,n)
$10,000 = R (PVIFA 12%,5)
$10,000 = R (3.605)
R = $10,000 / 3.605 = $2,774
Amortizing a Loan Example

82. End of
Year
Payment Interest Principal Ending
Balance
0 — — — $10,000
1 $2,774 $1,200 $1,574 8,426
2 2,774 1,011 1,763 6,663
3 2,774 800 1,974 4,689
4 2,774 563 2,211 2,478
5 2,775 297 2,478 0
$13,871 $3,871 $10,000
[Last Payment Slightly Higher Due to Rounding]
Amortizing a Loan Example

83. 2. Calculate Debt Outstanding – The quantity of outstanding debt may
be used in financing the day-to-day activities of the firm.
1. Determine Interest Expense – Interest expenses may reduce taxable income of the firm.
Usefulness of Amortization