The document outlines control engineering concepts focused on first and second-order systems, specifically discussing step and impulse responses using MATLAB functions. It includes MATLAB code for analyzing a closed-loop speed tachometer control system with external disturbances, detailing system parameters and output characteristics. The results indicate the steady-state error and system response over time for the specified control setup.

1. Control Engineering Lab
Engr. Adnan Rasheed

2. A first-order system without zeros
The Step Response of the above system will be,

7. 2nd Order Control Systems

10. Damping Cases (2nd Order) w.r.t Step
Responses

13. MATLAB Control Functions
step (num,den) : To plot the step response of the system
impulse(num,den) : To plot the impulse response of the system.
[y,x,t]=step(num,den): To store the values of the step response
function in an array.
ym=max(y): To get the maximum amplitude of a response value.
ys = dcgain(num,den) : To get the d.c. gain of the system (steady state
value)
yovrsht = (ym-yt)/ys * 100; To calculate the % over shoot.

14. Example 5.2.
5.2 Closed-loop speed tachometer control system
R(S) is the input voltage
w(S) is the output angular movement of motor
Td(S) is the external disturbance signal
5.2.1 Requirement:
Analyze under external Disturbance Closed loop with
feedback is better:

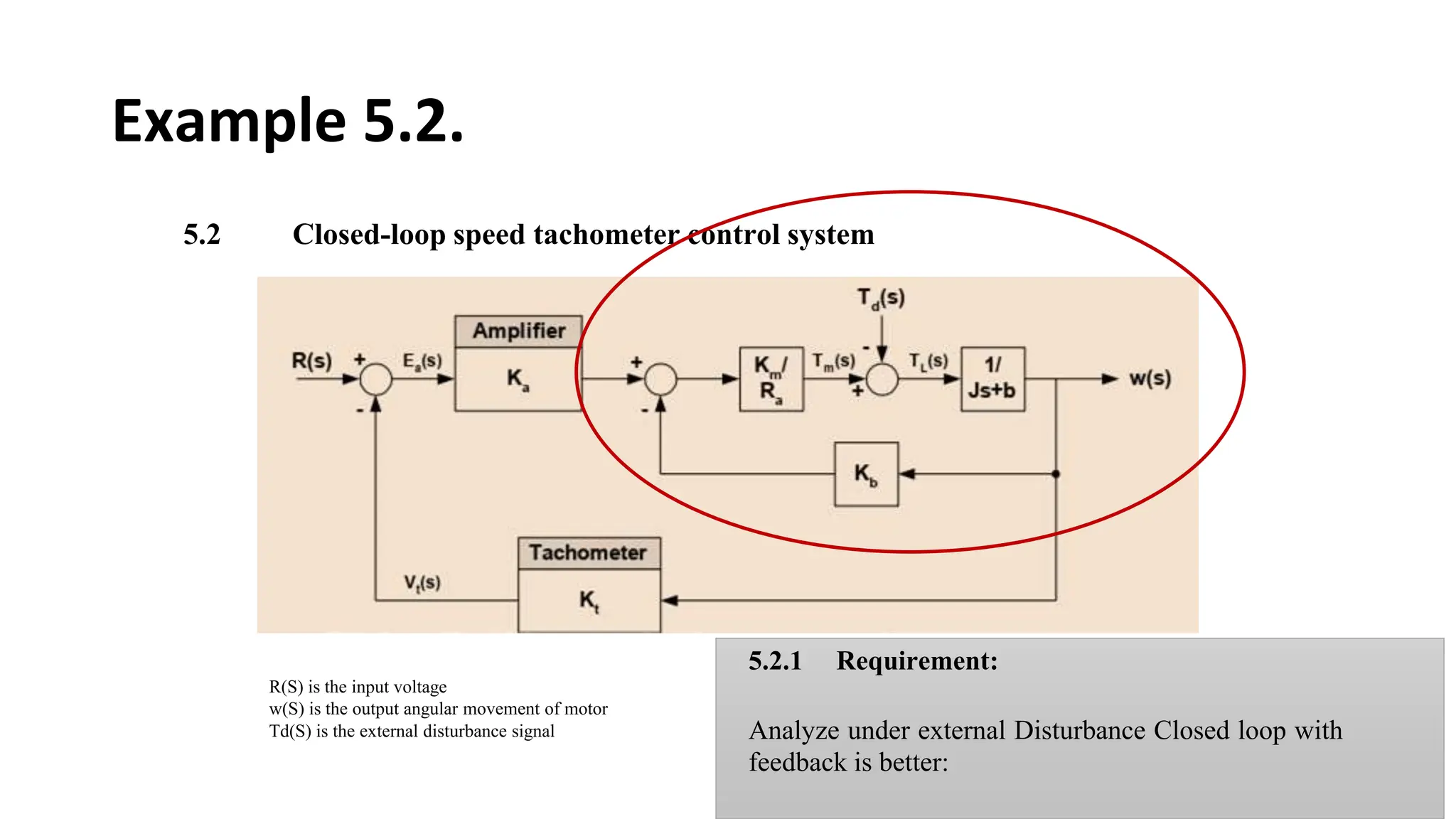
15. 5.2.1 MATLAB Code for the Open-loop without
tachometer feedback of the above example
(Case-I)
• % ---------------------------------------------------------------------------MEEN-4263 Control Engineering Lab -------------------------------------------------------------
• % Author : Engr. Adnan Rasheed
• % Date : xxxxxxxx
• % Lab No. : 5
• % Class : BEMTS VI (A & B)
• % File name : opentach.m
• % Description : The function implements the speed tachometer example.
• %------------------------------------------------------------------------------------- % Define Tachometer control system parameters
• Ra = 1; Km = 10; J= 2; b = 0.5; Kb = 0.1; Ka = 54; Kt = 1;
• num1 = [1]; den1 = [J b]; % Define G(s)= 1 / Js+b
• num2 = [Km*Kb/Ra]; den2 = [1]; % Define H(s) = Km*Kb/Ra
• [num,den] = feedback(num1,den1,num2,den2); % Find the T(S)= w(s) / Td(s)
• num = -num % Change the sign of T(s) since Td(s) is negative
• printsys(num,den); % print the final T(S)
• [step_resp,x,t] = step(num,den); % Compute response to step disturbance
• figure plot(t,step_resp); % plot step response
• title('Open-loop Disturbance Step Response');
• xlabel('time[sec]'); ylabel('speed'); grid;
• Final_val = step_resp(length(t)) % Find steady-state error, last value of output
• %-------------------------------------------------------------------------------------
• % End Function
• %-------------------------------------------------------------------------------------

16. 5.2.3 MATLAB Code for the Open-loop without
tachometer feedback of the above example
(Case-I)
The resulting system reduced to the following taking step Td(s):
Figure 5.3: Open-Loop system Disturbance Step Response
The approximate steady state
value is:
w(7) = -0.66 rad/s
at t = 7 sec